ФАЗОВАЯ МОДУЛЯЦИЯ

При фазовой модуляции в соответствии с модулирующим сигналом изменяется фаза высокочастотного колебания (2.3.1)

(2.3.27)

где - индекс фазовой модуляции. При модуляции чистым тоном имеем

(2.3.28)

Сравнивая (2.3.28) и (2.3.20), можно заметить, что выражения для ФМ и ЧМ по форме записи одинаковы. Однако при ФМ в аргумент тригонометрической функции входит модулирующая функция u(t), а при ЧМ - интеграл от нее. При модуляции чистым тоном и одинаковых индексах модуляции разницы в форме и спектрах этих колебаний нет. Различие между ними заключается в различном определении индексов модуляции. При фазовой модуляции индекс модуляциипропорционален амплитуде модулирующего напряжения и не зависит от его частоты. При ЧМ величина девиациипропорциональна амплитуде модулирующего напряжения, а индекс модуляциизависит от частоты модуляции. Появление множителяозначает необходимость введения соответствующих корректирующих цепей: если для приема ФМ сигналов используется приемник ЧМ сигналов, то в последнем необходимо добавить интегрирующее звено.

С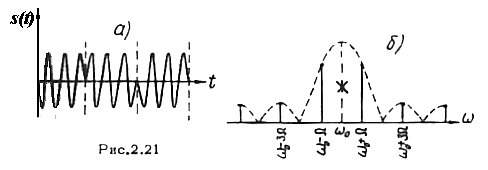ущественное различие между ФМ и ЧМ обнаруживается при сложных модулирующих сигналах, т.е. когда модулирующая функция обладает богатым спектром. В качестве примера можно рассмотреть случай фазовой манипуляции (рис.2.21 а). Как отмечалось выше, такой сигнал можно рассматривать как АМ колебание с подавленной несущей, спектр которого показан на рис. 2.21 б. (ср. с рис.2.20).

Этот же результат можно получить, если рассматривать ФМ колебание как сумму двух АМ колебаний, одно из которых сдвинуто по фазе на 180 и по времени на величину . Поэтому, согласно (2.1.29), можно написать

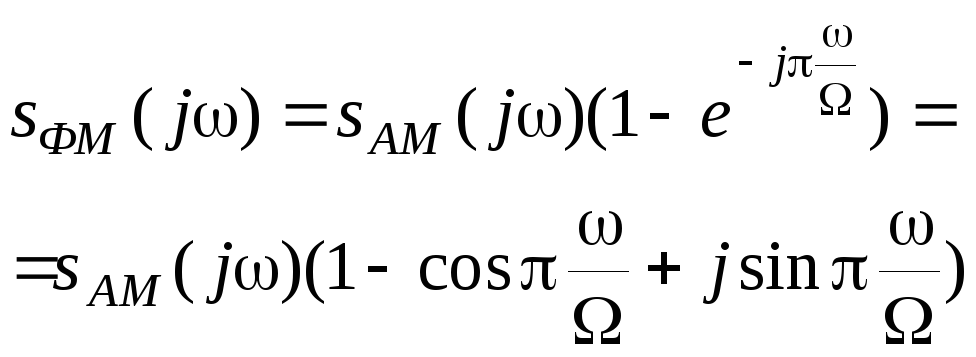(2.3.29)

где к=0;1;2;...

При целом числе периодов высокочастотного колебания на интервале получим

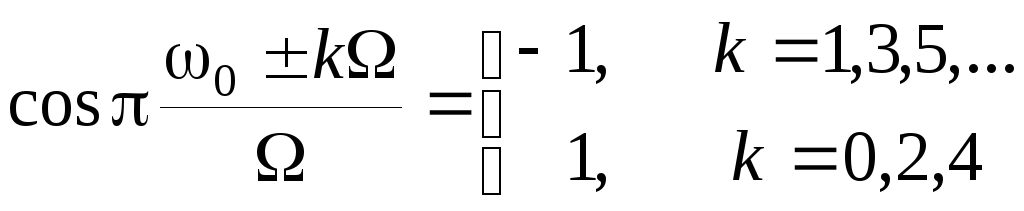
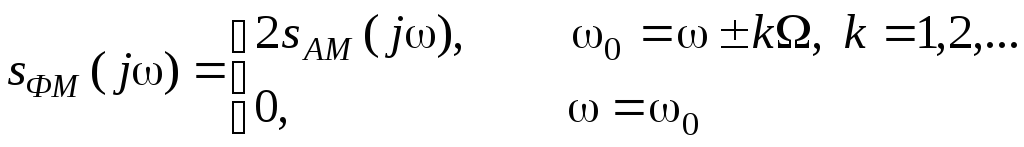
Таким образом, приходим к результату, показанному на рис. 2.21 б.

В заключение этого раздела заметим, что фазовую и частотную модуляцию часто называют угловой модуляцией. Однако при объединении их под одним названием необходимо помнить, что между ними в общем случае имеются существенно различия как в форме колебаний, так и их спектрах.

ИМПУЛЬСНАЯ МОДУЛЯЦИЯ

В рассмотренных выше видах модуляции в качестве переносчика использовалось гармоническое колебание. Однако в качестве переносчика можно использовать также периодическую последовательность коротких прямоугольных импульсов. Это следует из рассматриваемой ниже теоремы Котельникова, согласно которой функцию, имеющую ограниченный спектр, можно полностью охарактеризовать ее мгновенными значениями, взятыми через определенный интервал времени.

,

где - ширина спектра сигнала. При использовании в качестве переносчика периодической последовательности прямоугольных импульсов возможны следующие виды импульсной модуляции: по амплитуде (АИМ), ширине или длительности (ШИМ) (рис.2.22), по частоте (ЧИМ) и фазе (ФИМ).

Немодулированная последовательность импульсов представляется рядом Фурье (2.2.12). Для получения спектра сигнала при импульсной модуляции в этом случае необходимо подставить соответствующее выражение модулируемого параметра. В качестве примера рассмотрим здесь амплитудно-импульсную модуляцию (АИМ) чистым тоном. В этом случае по закону управляющего сигнала изменяется амплитуда и, следовательно, площадь импульсов:

.

Подставив это выражение в (2.2.12), получим

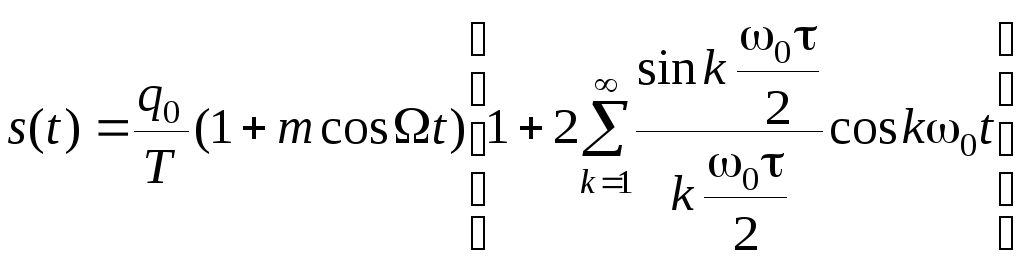(2.3.30)

После тригонометрических преобразований находим

(2.3.31)

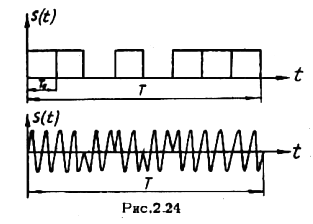
Спектр этого колебания показан на рис.2.23.

С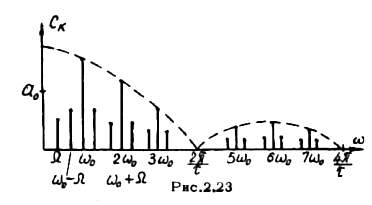равнивая его со спектром обычной АМ, замечаем, что при АИМ каждая частотная составляющая немодулированной последовательности импульсов модулируется независимо как изолированная ''несущая''. Это позволяет осуществлять демодуляцию при АИМ с помощью фильтра, пропускающего одну из ''несущих'' с боковыми частотами и обычного амплитудного детектора. Кроме того, в спектре сигнала с АИМ содержится составляющая низкочастотного модулирующего сигнала с частотой Ω. Следовательно, демодуляция при АИМ может быть осуществлена обычным фильтром нижних частот, пропускающим низкочастотное колебаниеu(t). 0днако выделение модулирующего сигнала при обоих способах детектирования возможно, как это видно из рис. 2.24, лишь при или. Обычно на практике частоту следования импульсов берут равной

где - максимальная частота в спектре модулирующего сигнала.

Аналогичным образом можно определить спектры и при других видах импульсной модуляции. Из-за громоздкости расчетов здесь они не приводятся. Заметим только, что при импульсных видах модуляции ширина спектра сигнала практически не висит от вида модуляции и определяется в основном длительностью и формой импульсов.

§ 2.4 Дискретизация детерминированных сигналов

ОРТОГОНАЛЬНЫЕ РАЗЛОЖЕНИЯ ФУНКЦИЙ

Широко известно использование аппарата Фурье для гармонического анализа детерминированных сигналов, при котором исходная функция разлагается в ряд по элементарным тригонометрическим функциям. Однако аппарат Фурье не является единственным. Можно заданную в интервале времени функциюf(t) разлагать в ряд по любым другим функциям , принятыми в качестве элементарных:

(2.4.1)

Сходимость этого ряда почти всегда обеспечивается. Задача разложения всегда сводится к выбору функций и определению коэффициентов разложения.

Коэффициенты разложения Ск наиболее легко определяются, если функции обладают свойством ортогональности. Функции называются ортогональными, если для них выполняется условие

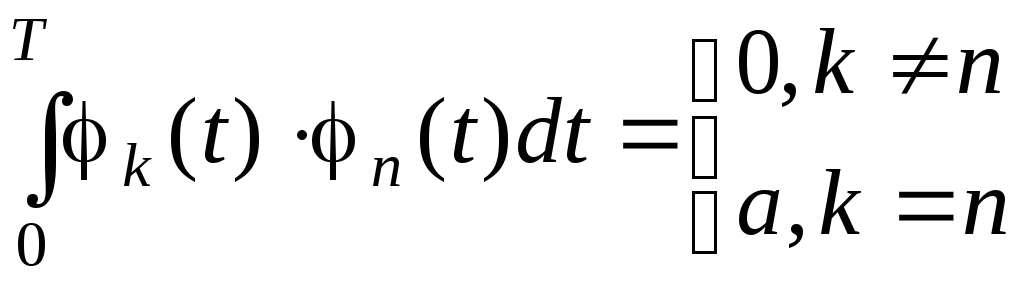(2.4.2)

Умножая левую и правую части выражения (2.4.1) на и интегрируя на интервале , с учетом ортогональности получим

(2.4.3)

Второе условие, которым необходимо руководствоваться при выборе функций разложения, заключается в упрощении анализа при теоретических исследованиях.

Для точного воспроизведения функции при представлении ее в виде ряда необходимо суммировать в общем случае бесконечное число членов. В некоторых случаях допустимо представление функции с некоторой погрешностью. При этом в разложении (2.4.1) можно ограничиться конечным числом членов:

(2.4.4)

Погрешность представления функции удобно оценивать величиной среднеквадратичной ошибки

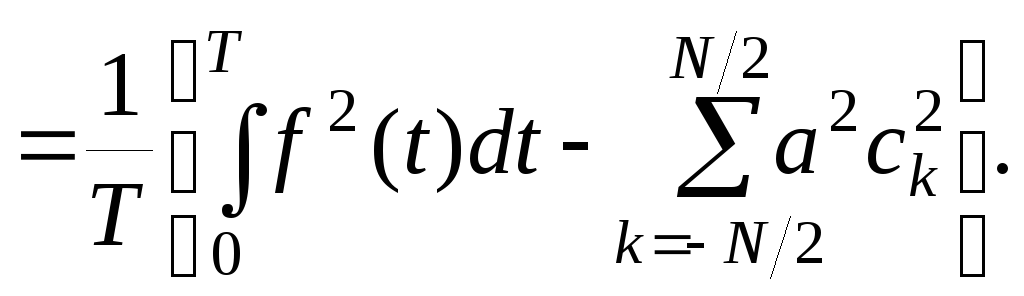(2.4.5)

При выборе функций разложения в этом случае необходимо руководствоваться условием обеспечения минимума ошибки при заданном числе членов ряда. При величина среднеквадратичной ошибка стремится к нулю, так как

(2.4.6)

Последнее выражение аналогично равенству Парсеваля, используемому в аппарате Фурье.

Таким образом, всякую функцию с некоторой погрешностью можно представить в виде ряда с конечным числом членов. Представление непрерывного колебания в виде набора конечного числа функций или чисел называют иногда дискретизацией.

Возможность представления функции в виде конечного ряда позволяет осуществить следующий способ передачи некоторого сигнала s(t). На передающем конце сигнал s(t) можно разложить в ряд по выбранным функциям и передавать не сигнал, а лишь коэффициенты разложения. На приемном конце, имея генераторы функций, по принятым коэффициентам можно восстановить переданный сигнал. Следовательно, с этой точки зрения в качестве функций разложения необходимо выбирать такие, которые легко генерировать.

Ниже рассматривается два вида ортогональных разложений: разложение Фурье по гармоническим функциям и разложение Котельникова по функциям отсчетов.

ДИСКРЕТИЗАЦИЯ ФУНКЦИЙ РЯДАМИ ФУРЬЕ

Рассмотренное выше в § 2.1 представление сигналов в виде ряда Фурье является типичным примером ортогонального разложения. Семейство тригонометрических функций 1, ,,,, …,,, … является ортогональным на интервале:

(2.4.7)

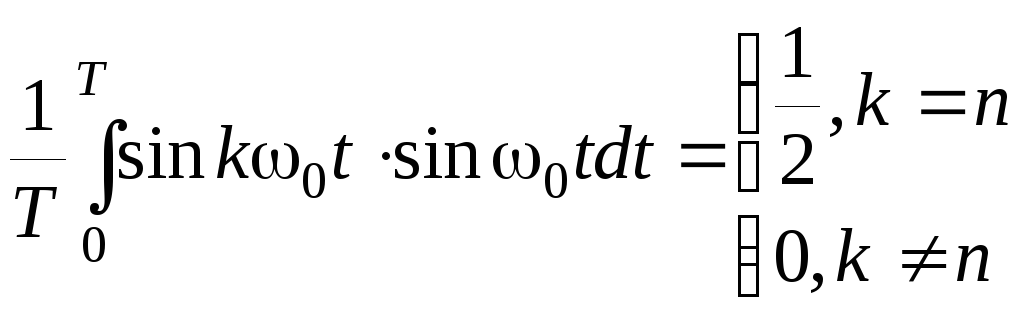
где

Остановимся на некоторых особенностях использования рядов Фурье. Обычно в ряд Фурье принято разлагать периодические функции, а для непериодических функций использовать интеграл Фурье. Однако в теоретических исследованиях используют представление в виде ряда Фурье и непериодических сигналов. Такой переход от интеграла к ряду Фурье приводит к тому, что непериодическая функция длительностью Т вне заданного интервала периодически продолжается с периодом Т. Такая замена непериодической функции периодической в общем случае не всегда допустима. Однако, в технике связи широко используются синхронные системы связи. Синхронная работа предполагает, что в месте приема известны начало и длительность сигнала, и, следовательно, возможна установка "нулевых начальных условий" в момент окончания сигнала. В этих условиях устраняется влияние периодического продолжения непериодического сигнала, и указанная замена при анализе прохождения сигналов через системы связи не приводит к ошибкам. Таким образом, в указанных условиях любой сигнал можно характеризовать как непрерывным, так и дискретным спектром.

Для реальных сигналов связи спектр является быстро убывающей функцией частоты. Поэтому часто бывает возможным ограничиться конечным числом членов в ряде Фурье

(2.4.8)

при достаточной точности представления сигнала. Если приемлемая точность обеспечивается при числе гармоник, равном N/2, то полоса частот, необходимая для передачи такого сигнала (без постоянной составляющей), равна

(2.4.9)

Если на приемной стороне имеются управляемые генераторы гармонических составляющих, то для восстановления сигнала необходимо передать

(2.4.10)

чисел, определяющих коэффициенты разложения.

Заметим, что для некоторых сигналов представление в виде конечного ряда может быть точным, например, для сигналов, составленных из N/2 гармоник или отрезка одного гармонического колебания, если длительность сигнала кратна период основной гармоники.

Величина В, равная удвоенному произведению длительности сигнала на ширину спектра частот, называется базой сигнала. Как известно из теории спектров, для наиболее часто встречающихся сигналов в виде отдельных импульсов произведение длительности на ширину спектра есть величина постоянная, имеющая порядок единицы: . Для таких сигналов, называемых простыми или узкополосными, база равна 2.

В качестве сигналов можно использовать и такие, которые являются комбинациями простых сигналов (рис.2.24).

Эти комбинации чаще всего представляют собой случайную последовательность простых сигналов. Такие сигналы называются составными или сложными. Для сложных сигналов ширина спектра будет той же, что и для простых, а длительность и соответственно произведение будет больше. Сигналы, для которых база, называются широкополосными и будут рассмотрены ниже.

В заключение отметим, что представление сигналов в виде ряда Фурье весьма удобно при исследовании прохождения сигналов через различные линейные цепи. Ряд Фурье из всех возможных ортогональных разложений обеспечивает наименьшую погрешность представления при заданном числе членов разложения N. Однако ряд Фурье неудобен с реализационной точки зрения, так как операции гармонического анализа, а тем более синтеза технически осуществить довольно трудно.

ПРЕДСТАВЛЕНИЕ ФУНКЦИЙ В ВИДЕ РЯДА КОТЕЛЬНИКОВА

Реальные сигналы имеют ограниченную полосу частот. Такие сигналы обладают замечательным свойством, впервые уставленным В. А. Котельниковым и выраженным в его теореме, играющей фундаментальную роль в теории и технике связи.

Если в общем случае непрерывная функция времени определяется на конечном интервале бесчисленным множеством своих мгновенных значений (рис.2.25), то функции времени с ограниченным спектром согласно теореме Котельникова на конечном интервале определяются конечным множеством своих значений.

Отсутствие в функции частот выше некоторой граничной накладывает определенные ограничения на ее изменение в достаточно малом интервале времени . Поэтому через точки, изображающие мгновенные значения функции и взятые через определенный интервал времени друг от друга, можно провести кривую одним единственным способом.

Теорему В. А. Котельникова можно сформулировать в следующем виде:

"Любая функция f(t), спектральная плотность которой отлична от нуля в полосе частот , полностью определяется последовательностью своих мгновенных значений, взятых в дискретных точках через интервалы времени. Значения функции в любой промежуточной точке определяются выражением

(2.4.11)

где - значения непрерывной функции в дискретных точках отсчета.''

Последнее выражение называется рядом Котельникова, коэффициенты разложения которого представляют собой отсчеты функции, а функциями разложения являются так называемые функции отсчетов

(2.4.12)

Эти функции обладают свойством

(2.4.13)

Т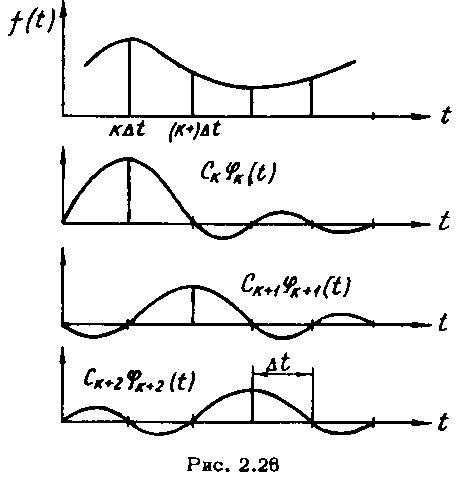аким образом, в момент временисумма ряда (2.4.11) определяется лишьk-ым слагаемым, все остальные члены ряда в этот момент времени обращаются в нуль. Разложение функции в ряд Котельникова иллюстрируется на рис.2.26.

Функции отсчета ортогональны на бесконечном интервале времени, т.е.

(2.4.14)

Энергия сигнала через его отсчетные значения выражается следующим образом

(2.4.15)

Перейдем теперь к доказательству теоремы Котельникова. Пусть спектральная плотность функции f(t)

(2.4.16)

отлична от нуля в полосе частот . Тогда для этой функции обратным преобразованием Фурье получим

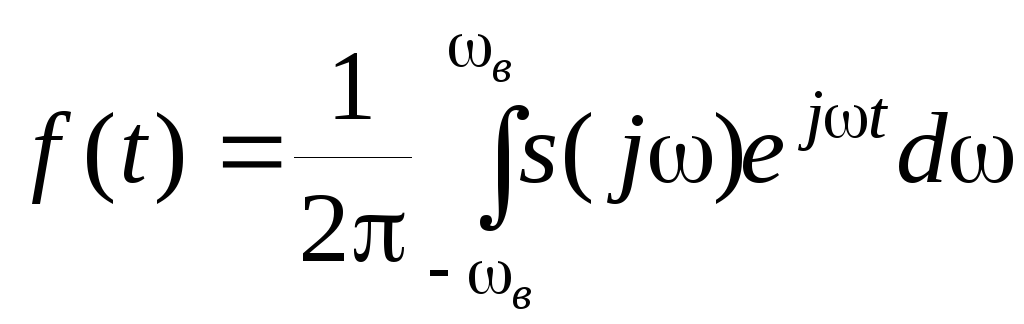(2.4.17)

Спектральную функцию , не содержащую периодических составляющих, на интервалеможно разложить в ряд Фурье с периодом,

(2.4.18)

коэффициенты которого определяются выражением

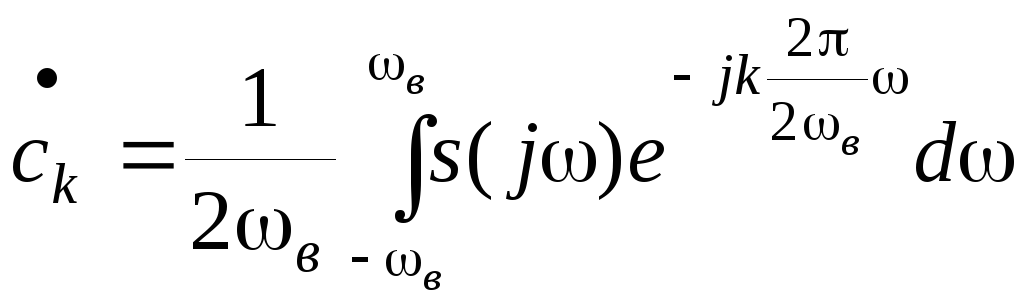(2.4.19)

Сравнивая (2.4.19) и (2.4.17) замечаем, что

(2.4.20)

Поэтому ряд (2.4.18) можно запасать в виде

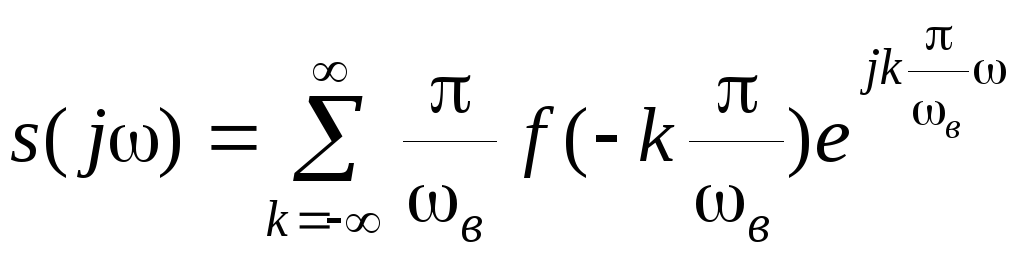(2.4.21)

Замечаем, что спектр функции f(t) однозначно определяется ее отсчетами , взятыми через интервал времени

(2.4.22)

Подставляя (2.4.21) в (2.4.17) и меняя порядок суммирования и интегрирования, получим

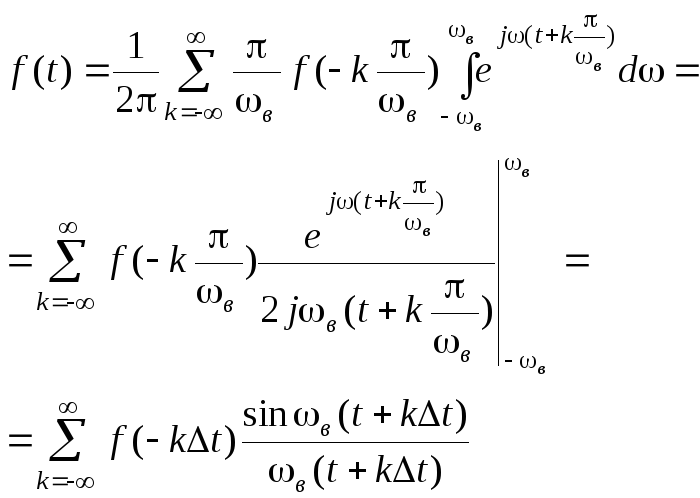(2.4.23)

Меняя в последнем выражении знак у индекса к, что изменит значения суммы, окончательно находим

(2.4.24)

что совпадает с (2.4.11).

ИСПОЛЬЗОВАНИЕ ТЕОРЕМЫ КОТЕЛЬНИКОВА ДЛЯ ПЕРЕДАЧИ СИГНАЛОВ СВЯЗИ

Разложение Котельникова было получено при предположении, что спектр функции ограничен частотой , т.е. функция имеет бесконечную длительность. Реальные сигналы имею бесконечную длительность и, следовательно, теоретически бесконечный спектр. Однако для них можно указать некоторую полосу частот, в которой сосредоточена основная мощность сигнала и которая содержит всю существенно необходимую информацию о сигнале. Разложение Котельникова для сигналов конечной длительности (финитных сигналов) будет иметь характер приближения соотношения

(2.4.25)

где число N определяется длительностью сигнала:

т. е., как и при использовании ряда Фурье, равно базе сигнала.

Таким образом, передачу непрерывных сигналов с ограниченной полосой частот можно свести к передаче чисел – ее мгновенных значений в дискретных точках отсчета. Практически это может быть осуществлено следующим образом. На передающей стороне периодическая последовательность коротких импульсов модулируется по высоте (амплитуде) и поступает в канал. На приемном конце эта последовательность подается на идеальный (физически нереализуемый) фильтр нижних частот с равномерной амплитудно-частотнойи линейной фазовойхарактеристиками (рис.2.27).

Отклик такого фильтра на очень короткий импульс дельта-функцию определяется выражением

(2.4.26)

где t' – момент появления импульса на входе. Последовательность импульсов на входе' создает последовательность откликов на выходе с амплитудами, пропорциональными амплитудам импульсов на входе, т.е. обеспечивает воспроизведение модулирующего сигнала согласно (2.4.11).

На практике для восстановления сигнала (АИМ) используются реальные фильтры нижних частот с граничной частотой . Как следует из (2.3.31) и рис.2.23, в этом случае для выделения модулирующего сигнала необходимо частоту следования импульсоввыбирать из условия.

Теорема Котельникова лежит в основе всех видов импульсной модуляции и методов временного уплотнения каналов.

Теорема Котельникова позволяет также количественно подойти к оценке пропускной способности систем связи при заданных сигналах. Пусть, например, сообщение передается с помощью набора элементарных сигналов вида 'да' и 'нет'. Принимая за единицу пропускной способности канала число элементарных посылок за 1сек (эта единица называется ''бодом''), получим, что по каналу с полосой частот можно передавать не болеебод. Следовательно, в этом случае пропускная способность или, точнее, скорость передачи не может быть больше 2 бод на 1 Гц полосы частот.

ДИСКРЕТИЗАЦИЯ ФУНКЦИЙ ПО УРОВНЮ

Т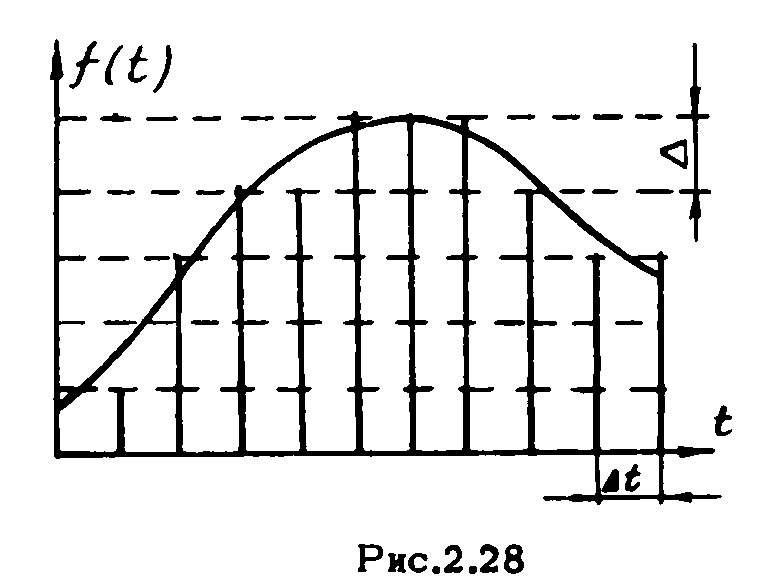еорема Котельникова позволяет перейти от передачи функции к передаче чисел, т.е. произвести дискретизацию функций по времени. Отсчеты функции представляют собой числа с непрерывной шкалой уровней. При наличии помех отсчеты в приемном устройстве воспроизводятся с некоторой погрешностью. Следовательно в этом случае нет необходимости использовать непрерывную шкалу уровней. Можно разбить весь диапазон изменения величины отсчетов наМ дискретных уровней, и передаваемое значение отсчета заменять его ближайшим дискретным значением (рис.2.28).

Такая замена непрерывной шкалы уровней дискретной называется квантованием. Разница между двумя соседними уровнями Δ называется шагом квантования. При квантовании сигнала неизбежно возникает погрешность, которая не превосходит половины шага квантования. Эта погрешность приводит к так называемым шумам квантования. При достаточном большом М шумы квантования могут быть сделаны малыми. При передаче телефонных сообщений, например, выбирают М = 128.

Если помеха в канале не превосходит половины шага квантования (в вероятностном смысле), то на приемной стороне принятое искаженное помехой значение будет отнесено к ближайшему дискретному уровню, соответствующему истинному уровню на передаче. Следовательно, квантование позволяет уменьшить влияние помех. Преимущества квантования особенно сильно проявляются при передаче на большие расстояния с использованием трансляций. Если между пунктами ретрансляции помеха не превосходит половины шага квантования, то сигнал можно точно восстановить (регенерировать). Регенерацию сигнала можно осуществлять сколь угодно раз. Если же сигнал передавался бы без квантования, то при многократной ретрансляции происходило бы накопление помех, и суммарный уровень помех на конце линии связи во много раз превосходил бы уровень шумов квантования.

Недостатком способа передачи с квантованием является то, то приемник должен различать большое число близко расположенных уровней. Техническая реализация при этом оказывается сложной. Поэтому в чистом виде квантованный сигнал не передают, а используют так называемую импульсно-кодовую модуляцию (КИМ), которая будет рассмотрена ниже.