
Лекции по ТЭС / Для студ.АЭС / Теоретич.материал / Гл 3 прод1
.docШИРОКОПОЛОСНЫЕ И УЗКОПОЛОСНЫЕ ПРОЦЕССЫ
Если
энергетический спектр случайного
процесса с непрерывным спектром
сосредоточен в относительно узкой
полосе частот
![]() около некоторой фиксированной частоты
около некоторой фиксированной частоты
![]() ,
(рис. 3.17а), причем
,
(рис. 3.17а), причем
![]() ,
то такой процесс называется узкополосным.
Если же указанное условие не выполняется,
то есть спектральная плотность средней
мощности сохраняет постоянное значение
до очень высоких частот (рис. 3.17 б), то
случайный процесс называется
широкополосным.
Для узкополосных и широкополосных
процессов корреляционные функции будут
значительно отличаться по длительности.
,
то такой процесс называется узкополосным.
Если же указанное условие не выполняется,
то есть спектральная плотность средней
мощности сохраняет постоянное значение
до очень высоких частот (рис. 3.17 б), то
случайный процесс называется
широкополосным.
Для узкополосных и широкополосных
процессов корреляционные функции будут
значительно отличаться по длительности.
Для широкополосного процесса согласно (3.3.10) корреляционная функция будет отличаться от нуля в узкой области значений τ около начала координат.
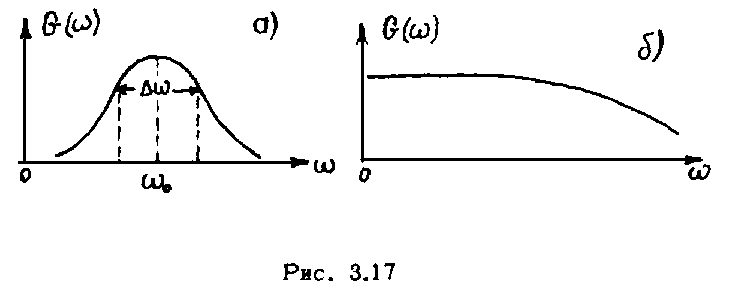 Полезной
математической идеализацией широкополосного
процесса является процесс, спектральная
плотность которого
Полезной
математической идеализацией широкополосного
процесса является процесс, спектральная
плотность которого
![]()
равномерна во всей области частот. Такой процесс по аналогии с белым светом называется белым шумом. Корреляционная функция белого шума равна
![]() (3.3.12)
(3.3.12)
т.е. представляет собой дельта-функцию в начале координат. Коэффициент корреляции для белого шума равен
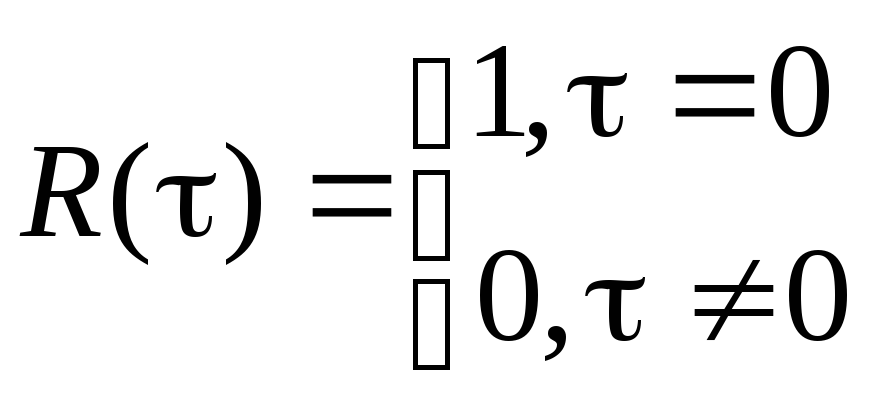 (3.3.13)
(3.3.13)
Следовательно, для белого шума значения процесса в любые сколь угодно близкие моменты времени не коррелированы. Поэтому белый шум иногда называют абсолютно случайным процессом.
Белый шум является математической идеализацией. В реальных процессах достаточно близкие значения практически зависимы. Кроме того, реальные процессы имеют конечную мощность, а для белого шума мощность процесса бесконечна. Однако на практике часто приходится рассматривать прохождение широкополосного процесса через различные радиотехнические устройства, полоса пропускания которых ограничена и много уже ширины энергетического спектра входного процесса. В этом случае замена реального процесса идеальным белым шумом не вносит существенных погрешностей, значительно упрощая при этом математические выкладки.
Отметим еще, что понятие "белый шум'' относится только к спектральной картине случайного процесса и не затрагивает вопроса о законах распределения. Как уже отмечалось выше, случайные процессы могут иметь одинаковые корреляционные функции и, следовательно, энергетические спектры, но различные законы распределения. Так и белые шумы с одинаковыми энергетическими спектрами могут иметь различные законы распределения.
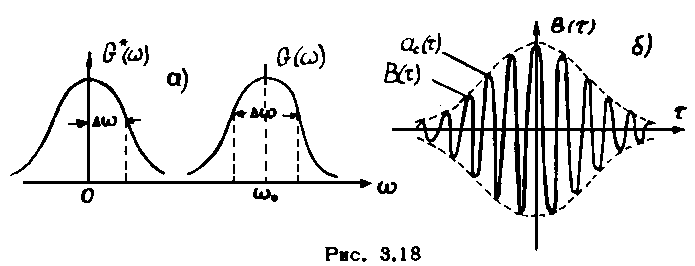
Определим
теперь корреляционную функцию
узкополосного случайного процесса со
спектральной плотностью
![]() (рис. 3.18)
(рис. 3.18)
![]() (3.3.14)
(3.3.14)
Вводя
вместо
![]() новую переменную интегрирования
новую переменную интегрирования
![]() ,
равную величине расстройки, вместо
(3.3.14), получим
,
равную величине расстройки, вместо
(3.3.14), получим
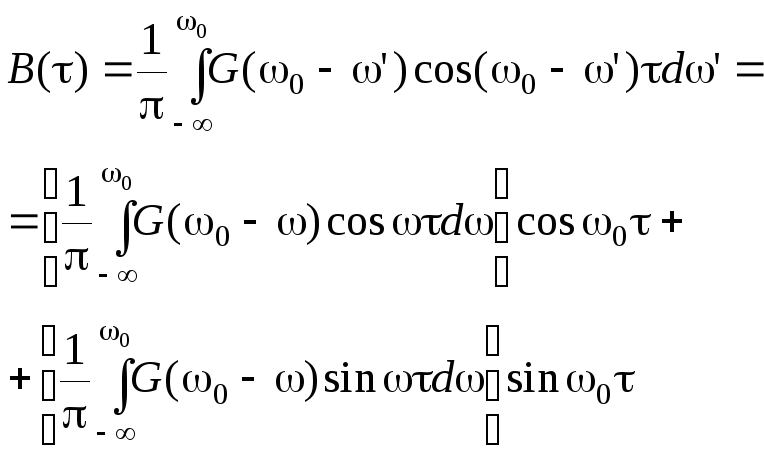
 (3.3.15)
(3.3.15)
Так
как для узкополосных процессов ширина
спектра мала по сравнению с
![]() ,
а функция
,
а функция
![]() расположена в области низких частот,
то верхние пределы интегрирования можно
распространить до бесконечности (здесь
рассматривается только положительная
ветвь
расположена в области низких частот,
то верхние пределы интегрирования можно
распространить до бесконечности (здесь
рассматривается только положительная
ветвь
![]() исходного процесса). Вводя обозначение
исходного процесса). Вводя обозначение
![]()
 (3.3.17)
(3.3.17)
для корреляционной функции узкополосного процесса окончательно находим
![]() (3.3.18)
(3.3.18)
Так
как энергетический спектр
![]() сосредоточен в узкой полосе частот
около
сосредоточен в узкой полосе частот
около
![]() ,
а спектр
,
а спектр
![]() расположен в низкочастотной области,
то функции
расположен в низкочастотной области,
то функции
![]() и
и
![]() будут медленно меняющимися функциями
по сравнению с
будут медленно меняющимися функциями
по сравнению с
![]() и
и
![]() .
.
Если
дополнительно предположить, что
энергетический спектр узкополосного
процесса симметричен относительно
центральной частоты
![]() ,
то энергетический спектр
,
то энергетический спектр
![]() будет симметричен относительно начала
координат. В этом случае функция
будет симметричен относительно начала
координат. В этом случае функция
![]() ,
так как для нее подынтегральное выражение
в (3.3.17) является нечетной функцией, и
,
так как для нее подынтегральное выражение
в (3.3.17) является нечетной функцией, и
![]() (3.3.19)
(3.3.19)
Следовательно,
корреляционная функция узкополосного
случайного процесса с симметричным
относительно средней частоты
![]() энергетическим спектром равна умноженной
на
энергетическим спектром равна умноженной
на
![]() корреляционной функции
корреляционной функции
![]() ,
которая соответствует низкочастотному
процессу со спектром
,
которая соответствует низкочастотному
процессу со спектром
![]() ,
полученному из исходного процесса
смешением спектра на величину
,
полученному из исходного процесса
смешением спектра на величину
![]() в область низких частот. Сказанное
иллюстрируется рис. 3.18 6.
в область низких частот. Сказанное
иллюстрируется рис. 3.18 6.
Интервал
корреляции узкополосного процесса
согласно (3.3.11) будет равен
![]() .
.
В качестве примера определим корреляционную функцию реализации процесса в виде отрезка гармонического колебания длительностью Т (рис. 3.19 а):
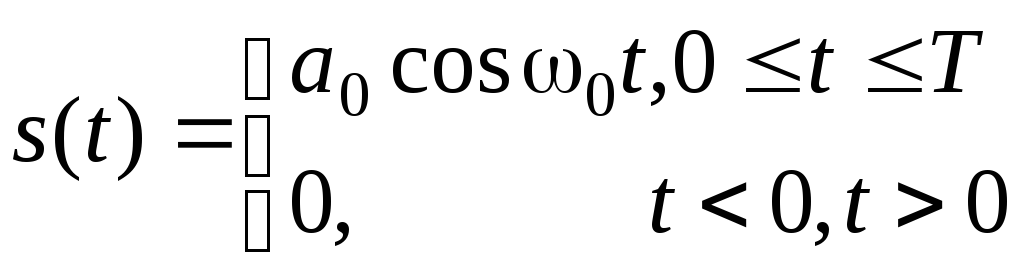 (3.3.20)
(3.3.20)
Амплитудно-фазовый спектр такого сигнала определяется выражением (2.2.21). Его энергетический спектр согласно определению (3.3.2) будет равен
 (3.3.21)
(3.3.21)
Корреляционная функция отрезка гармонического колебания будет равна
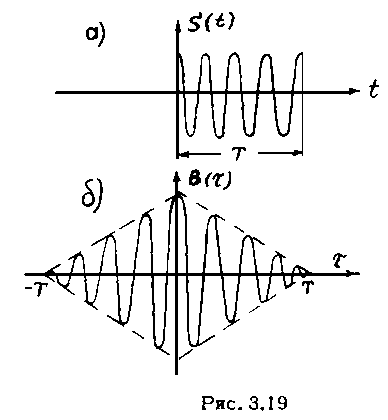
![]() (3.3.22)
(3.3.22)
Определение корреляционной функции согласно (3.3.22) требует использования теории вычетов и вызывает затруднения. Поэтому в рассматриваемом случае для вычисления корреляционной функции воспользуемся выражением
![]() (3.3.23)
(3.3.23)
Вычисление этого интеграла аналогично вычислению интеграла (3.2.27). В данном случае имеем
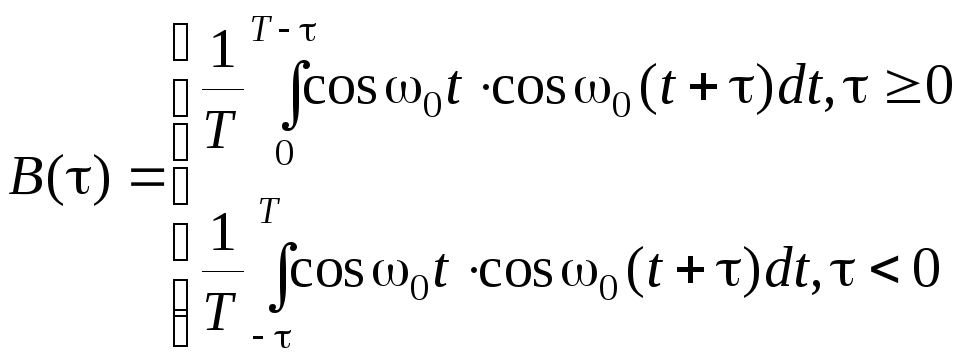 (3.3.24)
(3.3.24)
После тригонометрических преобразований и интегрирования получим
![]()
График полученной корреляционной функции показан на рис.3.19 6. Замечаем, что первый из сомножителей представляет собой корреляционную функцию одиночного прямоугольного импульса (3.2.31), т.е. огибающей радиоимпульса, спектр которой по форме совпадает со спектром радиоимпульса, но сдвинут в область низких частот.
§ 3.4 ПРОХОЖДЕНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ ЧЕРЕЗ ЛИНЕЙНЫЕ И НЕЛИНЕЙНЫЕ ЦЕПИ.
Рассмотрим
линейную инерционную систему с известной
передаточной функцией
![]() или импульсной реакцией
или импульсной реакцией
![]() .
Пусть на вход такой системы поступает
стационарный случайный процесс с
заданными характеристиками: плотностью
вероятности
.
Пусть на вход такой системы поступает
стационарный случайный процесс с
заданными характеристиками: плотностью
вероятности
![]() ,
корреляционной функцией
,
корреляционной функцией
![]() или энергетическим спектром
или энергетическим спектром
![]() .
Определим характеристики процесса
.
Определим характеристики процесса
![]() на выходе системы:
на выходе системы:
![]() ,
,
![]() и
и
![]() .
.
![]()
![]()


![]()
Наиболее
просто можно найти энергетический
спектр процесса на выходе системы.
Действительно, отдельные реализации
процесса на входе являются детерминированными
функциями, и к ним применим аппарат
Фурье. Пусть
![]() - усеченная реализация длительности Т
случайного процесса на входе, а
- усеченная реализация длительности Т
случайного процесса на входе, а
![]() (3.4.1)
(3.4.1)
-
ее спектральная плотность. Спектральная
плотность реализации
![]() на выходе линейной системы будет равна
на выходе линейной системы будет равна
![]() (3.4.2)
(3.4.2)
Энергетический спектр процесса на выходе согласно (3.3.3) будет определиться выражением
 (3.4.3)
(3.4.3)
т.е. будет равен энергетическому спектру процесса на входе, умноженному на квадрат амплитудно-частотной характеристики системы, и не будет зависеть от фазочастотной характеристики.
Корреляционная функция процесса на выходе линейной системы может быть определена как преобразование Фурье от энергетического спектра:
![]() (3.4.4)
(3.4.4)
Следовательно, при воздействии случайного стационарного процесса на линейную систему на выходе получается также стационарный случайный процесс с энергетическим спектром и корреляционной функцией, определяемыми выражениями (3.4.3) и (3.4.4). Мощность процесса на выходе системы будет равна
![]() (3.4.5)
(3.4.5)
В
качестве первого примера рассмотрим
прохождение белого шума со спектральной
плотностью
![]() через идеальный фильтр нижних частот,
для которого
через идеальный фильтр нижних частот,
для которого
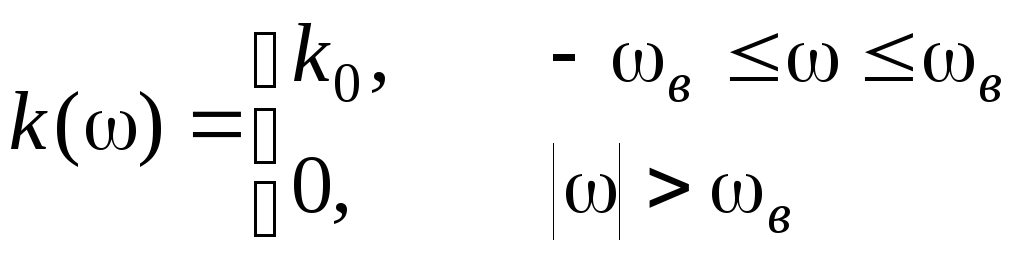 (3.4.6)
(3.4.6)
Согласно
(3.4.3) энергетический спектр процесса на
выходе будет иметь равномерную в полосе
частот
![]() спектральную плотность
спектральную плотность
![]() ,
а корреляционная функция будет
определяться выражением
,
а корреляционная функция будет
определяться выражением
 (3.4.7)
(3.4.7)
Мощность случайного процесса на выходе идеального фильтра нижних частот будет равна
![]() (3.4.8)
(3.4.8)

![]()
![]()

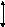
![]()
о



![]()
![]()
 пределяется
выражением:
пределяется
выражением:
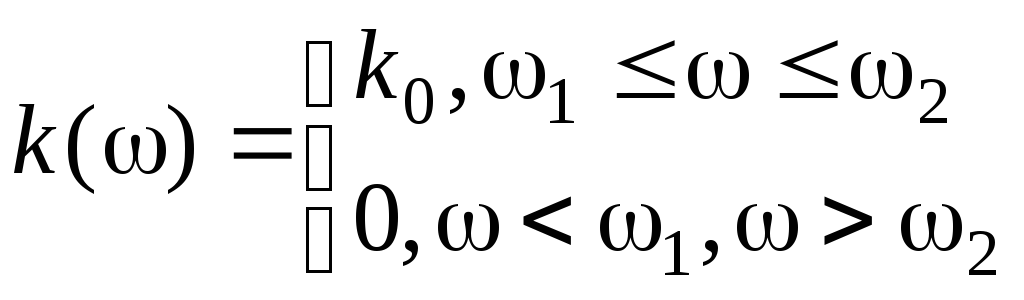 (3.4.9)
(3.4.9)
В этом случае
 (3.4.10)
(3.4.10)
Корреляционную функцию определим с помощью косинус-преобразования Фурье:
 (3.4.11)
(3.4.11)
где
![]() ,
,
![]()
Г рафик
корреляционной функции показан на рис.
3.22.
рафик
корреляционной функции показан на рис.
3.22.
Рассмотренные примеры показательны с той точки зрения, что они подтверждают установленную в § 3.3 связь между корреляционными функциями низкочастотного и узкополосного высокочастотного процессов с одинаковой формой энергетического спектра. Мощность процесса на выходе идеального полосового фильтра будет равна
![]() (3.4.12)
(3.4.12)
Закон распределения вероятностей случайного процесса на выходе линейной инерционной системы отличается от закона распределения на входе, и определение его является весьма сложной задачей, за исключением двух частных случаев, на которых здесь остановимся.
Если случайный процесс воздействует на узкополосную линейную систему, полоса пропускания которой много меньше ширины спектра, то на выходе системы имеет место явление нормализации закона распределения. Это явление заключается в том, что закон распределения на выходе узкополосной системы стремится к нормальному независимо от того, какое распределение имеет широкополосный случайный процесс на входе. Физически это можно объяснить следующим образом. Процесс на выходе инерционной системы в некоторый момент времени представляет собой суперпозицию отдельных откликов системы на хаотические воздействия входного процесса в различные моменты времени. Чем уже полоса пропускания системы и шире спектр входного процесса, тем большим числом элементарных откликов образуется выходной процесс. Согласно же центральной предельной теореме теории вероятностей закон распределения процесса, представляющего собой сумму большого числа элементарных откликов, будет стремиться к нормальному.
Из приведенных рассуждений следует второй частный, но весьма важный случай. Если процесс на входе линейной системы имеет нормальное (гауссово) распределение, то он остается нормальным и на выходе системы. В этом случае изменяются только корреляционная функция и энергетический спектр процесса.
НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
Рассмотрим
теперь задачу о прохождении случайного
процесса через нелинейную систему. В
общем случае эта задача весьма сложная,
но она значительно упрощается, когда
нелинейная система является безынерционной.
В безынерционных нелинейных системах
значения выходного процесса
![]() в данный момент времени определяются
значениями входного процесса
в данный момент времени определяются
значениями входного процесса
![]() в тот же самый момент времени. Для
нелинейных безынерционных преобразований
более простой задачей является определение
функций распределения на выходе в
гораздо более сложной – определение
корреляционной функции или энергетического
спектра.
в тот же самый момент времени. Для
нелинейных безынерционных преобразований
более простой задачей является определение
функций распределения на выходе в
гораздо более сложной – определение
корреляционной функции или энергетического
спектра.
Как отмечалось выше, n - мерная функция распределения случайного процесса по сути дела является функцией распределения n случайных величин, представляющих собой значения случайного процесса в n различных моментов времени, Определение законов распределения функционально преобразованных случайных величин является сравнительно простой задачей.
Рассмотрим
простейший пример одномерной случайной
величины. Пусть
![]() - плотность вероятности случайной
величины ζ,
которая подвергается нелинейному
преобразованию
- плотность вероятности случайной
величины ζ,
которая подвергается нелинейному
преобразованию
![]() .
Определим плотность вероятности
.
Определим плотность вероятности
![]() случайной величины η. Предположим, что
функция
случайной величины η. Предположим, что
функция
![]() такова, что обратная ей функция
такова, что обратная ей функция
![]() – однозначна.
– однозначна.
Если
случайная величина ζ находится в
достаточно малом интервале
![]() ,
то вследствие однозначной функциональной
зависимости между ζ и η случайная
величина η обязательно будет находиться
в интервале
,
то вследствие однозначной функциональной
зависимости между ζ и η случайная
величина η обязательно будет находиться
в интервале
![]() ,
где
,
где
![]() ,
вероятности этих событий должны быть
одинаковыми, т.е.
,
вероятности этих событий должны быть
одинаковыми, т.е.
![]() (3.4.13)
(3.4.13)
откуда находим
![]() (3.4.14)
(3.4.14)
Производная
в последнем выражении берется по
абсолютной величине, так как плотность
вероятности не может быть отрицательной.
Если обратная функция
![]() неоднозначная, т.е. имеет несколько
ветвей
неоднозначная, т.е. имеет несколько
ветвей
![]() ,
то для плотности вероятности с
использованием теоремы сложения
вероятностей можно получить
,
то для плотности вероятности с
использованием теоремы сложения
вероятностей можно получить
![]() (3.4.15)
(3.4.15)
Отметим, что для определения числовых характеристик нелинейно-преобразованных случайных процессов нет необходимости определять их плотности вероятностей. Действительно, в общем случае для начального момента k-го порядка имеем
![]() (3.4.16)
(3.4.16)
Но
согласно (3.4.13)
![]() и
и
![]() .
Поэтому последнее выражение можно
переписать
.
Поэтому последнее выражение можно
переписать
![]() (3.4.17)
(3.4.17)
Полученные
выражения (3.4.14) и (3.4.15) легко распространить
на случай нескольких величин. Приведем
здесь лишь окончательный результат для
двумерного случая. Если случайные
величины
![]() и
и
![]() имеют совместную плотность вероятностей
имеют совместную плотность вероятностей
![]() ,
то для случайных величин
,
то для случайных величин
![]() (3.4.18)
(3.4.18)
![]()
при однозначности обратных функций
![]()
![]()
совместная плотность вероятностей будет определяться выражением
![]() (3.4.19)
(3.4.19)
где величина
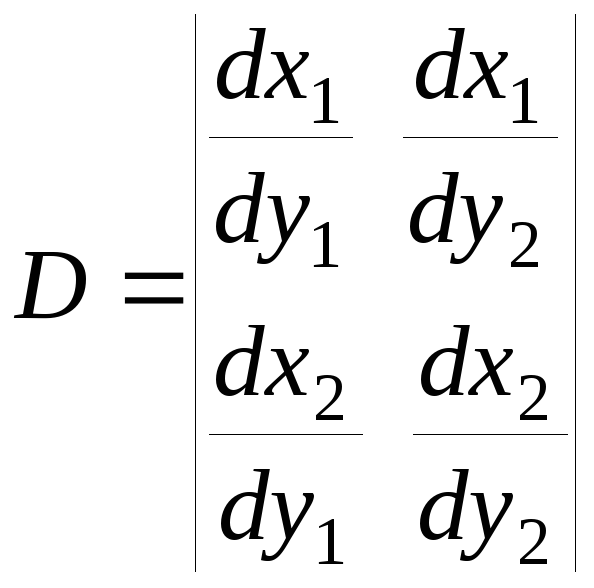 (3.4.20)
(3.4.20)
называется
якобианом преобразования и представляет
собой отношение элементарных площадей
![]() при переходе от одной системы координат
к другой. Если
при переходе от одной системы координат
к другой. Если
![]() ,
то справедливо равенство
,
то справедливо равенство
![]() (3.4.21)
(3.4.21)
где

