П РИМЕРЫ НЕЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ СЛУЧАЙНЫХ ПРОЦЕССОВ

В качестве первого примера рассмотрим квадратичное преобразование случайного процесса

которое осуществляется, например, безынерционным квадратичным детектором.

Обратные функции при квадратичном преобразовании имеют вид

где для краткости аргумент времени опущен. При этом

и(3.4.22)

Используя (3.4.15), для одномерной плотности вероятности случайного процесса находим

(3.4.23)

Если случайный процесс на входе имеет нормальное распределение вероятностей

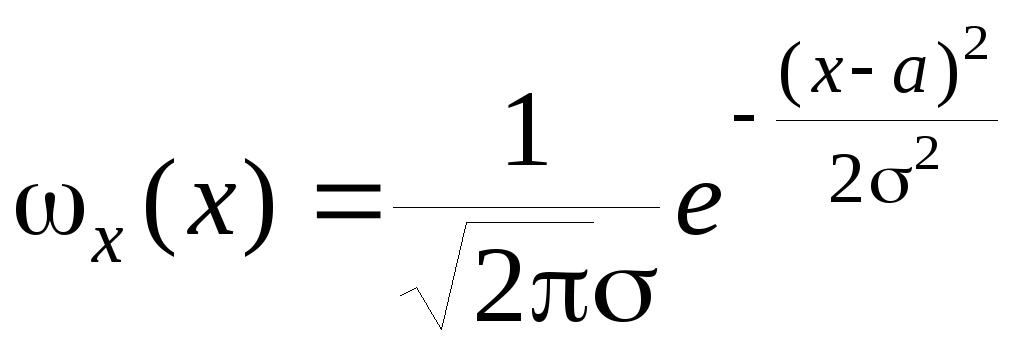(3.4.24)

то, используя (3.4.23) , для процесса на выходе квадратичного преобразователя получим

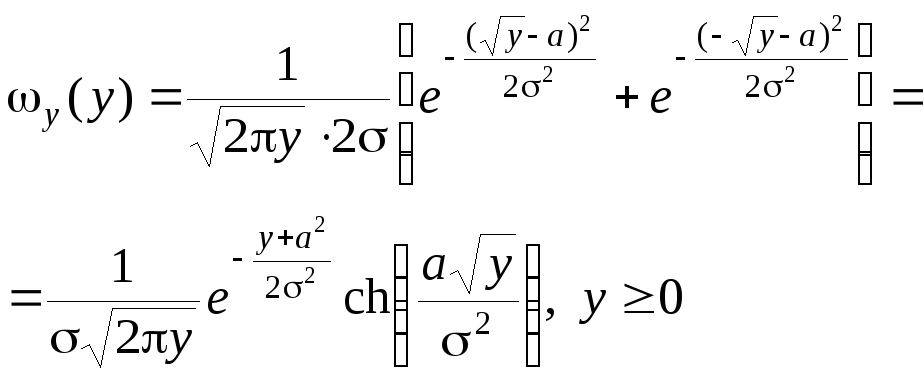(3.4.25)

Для нормального случайного процесса с нулевым средним значением выражение (3.4.25) упрощается:

(3.4.26)

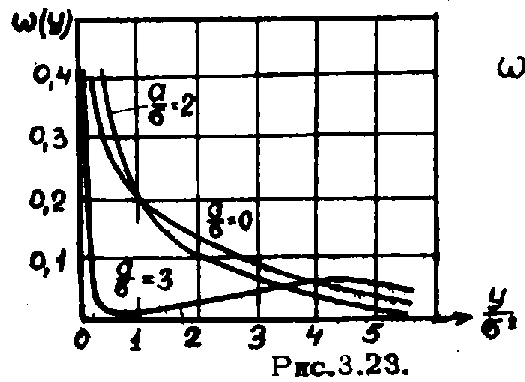
Графики полученной плотности вероятности для различных значений показаны на рис 3.23.

Определим теперь закон распределения вероятностей гармонического колебания.

(3.4.27)

полная фаза т которого является случайней и имеет равномерное распределение вероятностей в интервале :

(3.4.28)

Обратная функция в пределах от 0 до 2π в этом случае двузначна и при одинаковомy имеет два следующих значения (рис.3.24 а):

,(3.4.29)

Производные от обратной функции определяются выражением

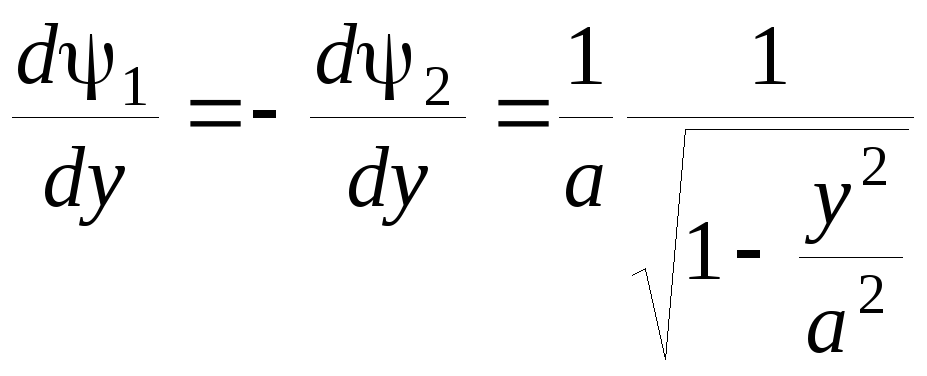(3.4.30)

Подставляя (3.4.28) и (3.4.30) в (3.4.15), для плотности вероятности гармонического колебания со случайной фазой получим

(3.4.31)

График полученной плотности вероятности показан на рис.3.24 б.

Рассмотрим еще следующий специальный вид двумерного преобразования случайных процессов, который представляет значительный интерес для радиотехнических приложений:

(3.4.32)

Г

еометрически это преобразование означает переход от случайных декартовых координат к случайным полярным координатам (рис.3.25).

Рис. 3.25

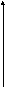
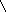
При таком преобразовании , а значения случайной величины φ заключены в пределах от 0 до 2π.

Обратные функции

и(3.4.33)

в этом случае однозначны. Якобиан преобразования согласно (3.4.20) будет равен

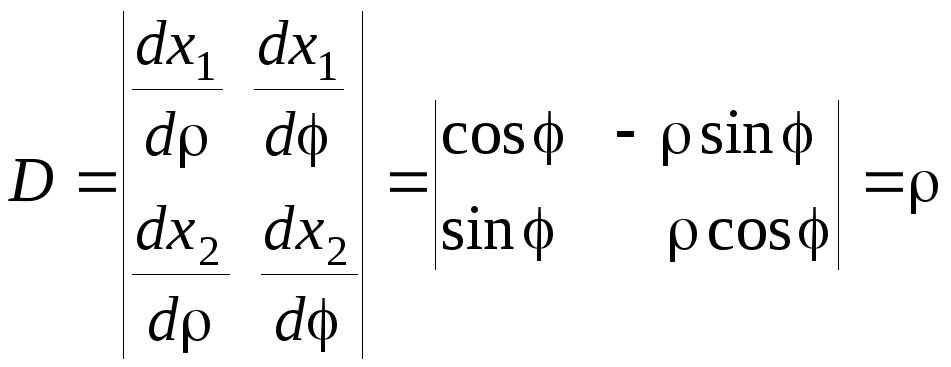(3.4.34)

Совместная плотность вероятностей случайных величин исогласно (3.4.19) будет определяться выражением

(3.4.35)

Одномерные функции распределения каждой из случайных величин ρ и φ можно получить, согласно правилам теории вероятностей, путем интегрирования двумерной функции распределения по ρ и φ соответственно:

(3.4.36)

(3.4.37)

Используем полученные выражения для случая, когда значения случайного процесса инезависимы и распределены по нормальному закону с параметрами () и () соответственно. Совместная плотность вероятностей в этом случае записывается в виде

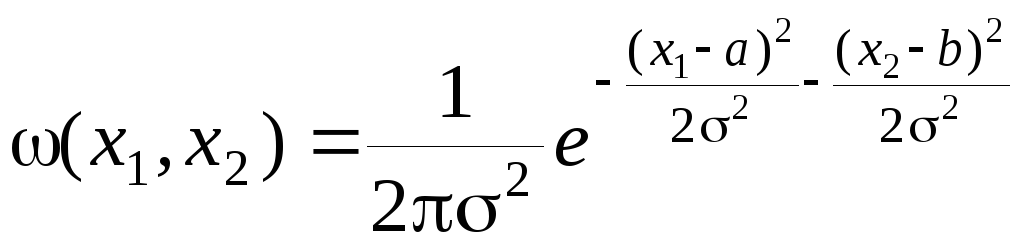(3.4.38)

Для случайных величин ρ и φ, используя (3.4.28), получим

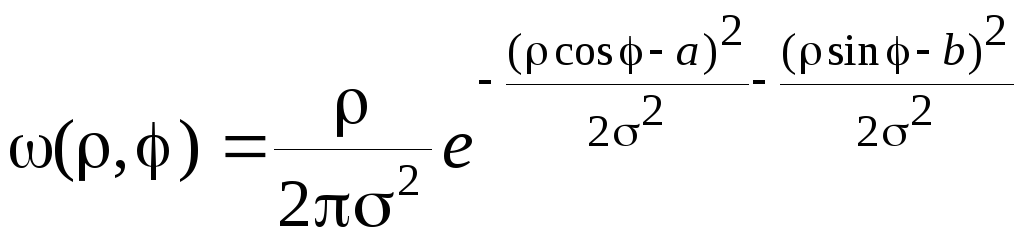(3.4.39)

Подставляя последнее выражение в (3.4.3 б) и производя интегрирование, для плотности вероятности амплитуды вектора (рис.3.20) получим

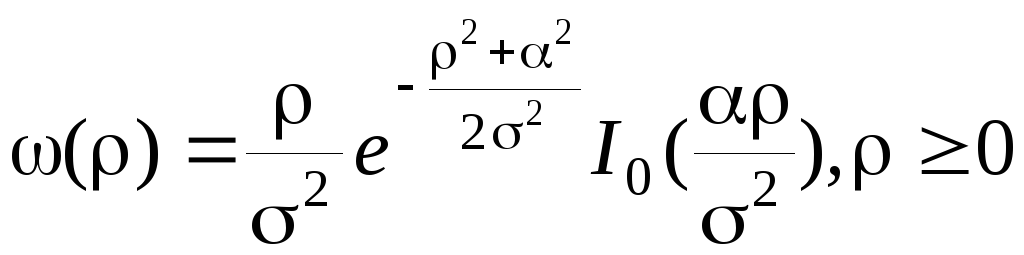(3.4.40)

где , а- функция Бесселя нулевого порядка от мнимого аргумента.

Если случайные величины иимеют нулевые средние значения, то плотность вероятности модуля вектора будет определяться выражением

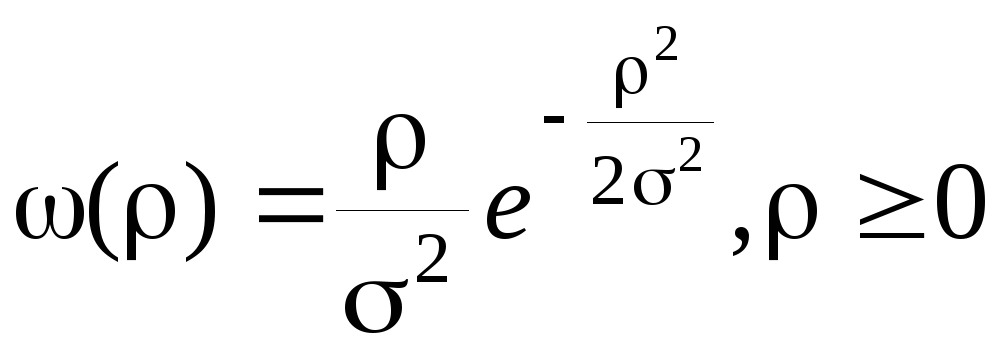(3.4.41)

Выражения (3.4.40) и (3.4.41) представляют собой плотности вероятностей для так называемых обобщенного и простого законов Релея соответственно. Графики плотности вероятности закона Релея для различных значений показаны на рис.3.26.

Аналогичным образом, используя (3.4.37), можно определить плотность вероятности для фазы случайного вектора φ. Однако, в общем случае выражение получается громоздким. Если же случайные величины иимеют нулевые средние значения, то плотность вероятности фазы будет определяться выражением

(3.4.42)

Следовательно, радиус-вектор, составляющие которого распределены нормально с нулевыми средними значениями, имеет простое релеевское распределение модуля и равномерное в интервале распределение фазы.

§ 3.5 Ортогональные разложения и комплексное представление случайных процессов

Рассмотренные в § 2.4 ортогональные разложения детерминированных сигналов можно использовать также для отдельных реализации случайных процессов. По отношению к случайному процессу в целом такие разложения имеют ту особенность, что коэффициенты разложения меняются от реализации к реализации. Следовательно, случайный процесс на интервале можно разложить в ряд по детерминированным функциям

(3.5.1)

где - среднее значение случайного процесса, а– коэффициенты разложения, являющиеся случайными величинами. Для случайных процессов сходимость ряда (3.5.1) необходимо понимать в среднеквадратичном смысле, т.е.

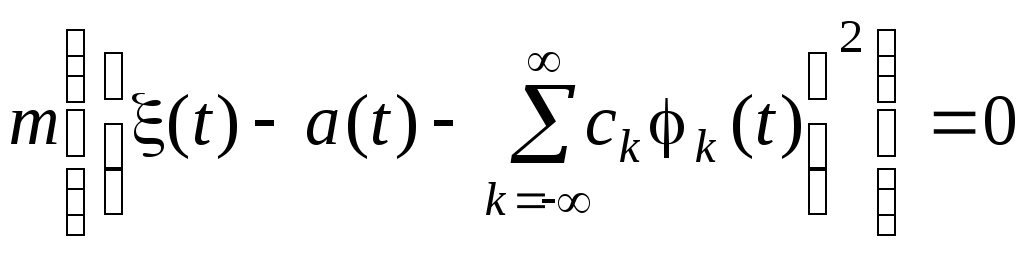(3.5.2)

При выборе функций разложения для случайных процессов необходимо учитывать то, что в общем случае коэффициенты разложения оказываютсякоррелированными. При теоретических исследованиях проще оперировать с некоррелированными коэффициентами. В этом случае задача отыскания функций усложняется и сводится к решению интегрального уравнения

(3.5.3)

связывающего функции разложения с корреляционной функцией случайного процесса . Представление случайного процесса в виде ряда (3.5.1) с некоррелированными и имеющими нулевые средние значения коэффициентами называется каноническим разложением.

Можно показать, что для белого шума любая система ортогональных функций обеспечат некоррелированность коэффициентов разложения.

В соответствии с (3.5.1) случайный процесс без постоянной составляющей можно представить в виде ряда Фурье

(3.5.4)

коэффициенты которого будут случайными, в общем случае коррелированными величинами. Для некоррелированности коэффициентов разложения в ряде Фурье необходимо выполнение одного из условий:

1) случайный процесс периодичен с периодом Т,

2) интервал разложения достаточно большой ;

3) случайный процесс представляет собой белый шум. Возводя обе части равенства (3.5.4) в квадрат и интегрируя на интервале 0-Т, с учетом ортогональности тригонометрических функций получим выражение

(3.5.5)

аналогичное равенству Парсеваля, в котором обе части являются случайными величинами.

Если случайный процесс не содержит частот выше , то он может быть представлен в виде ряда Котельникова

(3.5.6)

где

Выясним смысл теоремы Котельникова применительно к случайным процессам. Для низкочастотных процессов, рассматриваемых здесь, корреляционная функция обычно имеет слабо выраженный колебательный характер и в основном расположена выше оси абсцисс. В этом случае, опуская в выражения (3.2.23) знак модуля и используя (3.3.8), для интервала корреляции случайного процесса получаем приближенное выражение

(3.5.7)

Если случайный процесс имеет равномерную спектральную плотность мощности в полосе частот, то согласно (3.3.6)и.

Следовательно, интервал времени есть не что иное, как интервал корреляции, а отсчеты представляют собой ближайшие некоррелированные значения случайного процесса. При использовании ряда Котельникова для процесса длительностью Т получим выражение, аналогичное (3.5.5):

(3.5.8)

где

КОМПЛЕКСНОЕ ПРЕДСТАВЛЕНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ

Рассмотренное в § 2.5 комплексное представление сигналов можно распространить также на случайные процессы. Если случайный стационарный процесс не имеет постоянной составляющей, то с помощью преобразования Гильберта (2.5.3) можно образовать сопряженный ему случайный процесс

(3.5.9)

который будет также стационарным.

Образуя комплексный случайный процесс

(3.5.10)

получим

(3.5.11)

где случайные функции

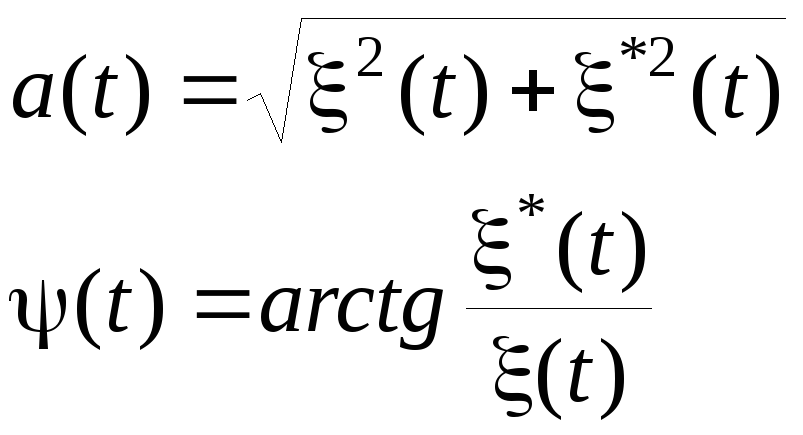(3.5.12)

можно рассматривать как огибающую и фазу случайного процесса. При таком представлении случайный процесс в целом можно рассматривать как гармоническое колебание, модулированное по амплитуде и фазе случайными функциями времени и.

Представление случайного процесса в виде огибающей и фазы оказывается весьма удобным, когда его энергетический спектр сосредоточен в относительно узкой полосе около средней частоты . В этом случае фазу случайного процесса после выделения детерминированного линейного членаможно представить в виде

(3.5.13)

Тогда для узкополосного случайного процесса можно записать

(З.5.14)

где (3.5.15)

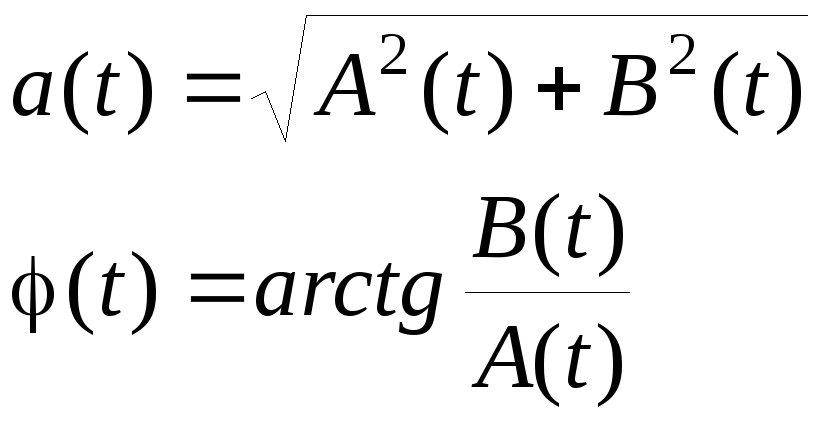(3.5.16)

Функции иназываются ''квадратурными огибающими'' случайного процесса и, каки, не содержат в своей записи линейного члена с частотой. Следовательно, узкополосный случайный процесс полностью характеризуется медленно меняющимися квадратурными огибающимии.

Между вероятностными характеристиками огибающих ,и, фазыи вероятностными характеристиками самого процесса существуют простые соотношения. Действительно, согласно свойству преобразования Гильберта (2.5.8) о спектре сопряженного сигнала, энергетические спектры и, следовательно, корреляционные функции процессовиодинаковы:

,(3.5.17)

откуда получим

Можно показать, что случайные процессы иив совпадающие (т.е. одинаковые) моменты времени некоррелированы, а для нормального процесса - независимы.

Корреляционные функции квадратурных огибающих определяются выраженном

(3.5.18)

Следовательно, дисперсии квадратурных огибающих равны между собой и равны дисперсии процесса :

(3.5.19)

Для узкополосного процесса с незначительной погрешностью нижний предел интегрирования в (3.5.18) можно распространить до . Если, кроме того, дополнительно предположить, что спектр узкополосного процесса симметричен относительно средней частоты, то получим

(3.5.20)

При этом квадратурные огибающие всегда оказываются некоррелированными, а для нормальных процессов – независимыми.

Корреляционная функция узкополосного случайного процесса с симметричным энергетическим спектром будет определяться выражением

(3.5.21)

При этом выясняется физический смысл введенной выше (3.3.17) функции , которая является корреляционной функцией для каждой из медленно меняющихся квадратурных огибающихи.