§ 2.6 Комплексное представление сигналов. Аналитические сигналы.

Как отмечалось выше, сигналы связи можно подразделить на радио- и видеосигналы. Обычно радиосигналы представляют собой узкополосный процесс, энергия которого сосредоточена в области несущей частоты. В общем случае при произвольном виде модуляции радиосигнал можно представить в форме

(2.5.1)

где функции иназываются соответственно огибающей и фазой радиосигнала.

При представлении сигналов в виде (2.5.1) возникает неоднозначность в выборе функций и, так как одному и тому же сигналу может быть поставлено в соответствие бесконечное множество пари. Например, при желании простейшее гармоническое колебание

можно представить в форме

где, как можно показать,

Из этого следует, что при нерациональном выборе аргумента сильно усложнилось выражение для функции, которая по существу не является огибающей в общепринятом смысле.

Чтобы исключить неоднозначность при определении огибающей и фазы, запись (2.5.1) доопределяют с помощью понятия ''аналитического'' сигнала. Напомним, что аналитической называется функция, которая непрерывна вместе со всеми своими производными. Многие сигналы связи не обладают таким свойством.

Все физические процессы в природе описываются действительными функциями времени. Однако всем известна широкая распространенность в электротехнике комплексного представления гармонических колебаний. При решении большого числа задач весьма эффективным оказывается комплексное представление и негармонических колебаний. Комплексное представление колебаний позволяет строить аналитические сигналы.

Можно показать, что комплексная функция действительного переменного t

(2.5.2)

является пределом аналитической функция комплексной переменной при, если функции и являются парой преобразований Гильберта:

(2.5.3)

В последних выражениях интегралы понимаются в смысле главного значения Коши. Функции и называются сопряженными по Гильберту, а сигнал (2.5.2) - аналитическим.

Выясним смысл преобразования Гильберта. Можно показать, что для тригонометрических функций

(2.5.4)

сопряженные по Гильберту функции соответственно имеют вид

(2.5.5)

В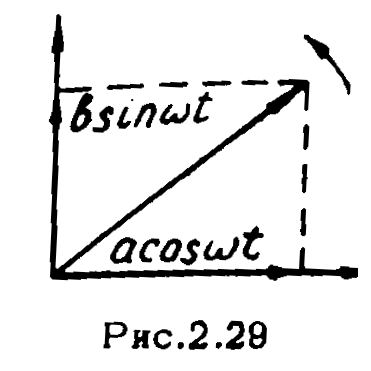общем случае для периодического сигнала

(2.5.6)

имеем (2.5.7)

Следовательно, сопряженный сигнал может быть получен из действительного сигналаs(t) поворотом фаз всех его частотных составляющих на угол против часовой стрелки (рис.2.29). Такая операция может быть осуществлена широкополосным фазовращателем.

Для непериодических сигналов спектральная плотность сопряженного сигнала связана со спектральной плотностью действительного сигнала соотношением

(2.5.8)

т.е. и в этом случае амплитудные спектры сигналов s(t) и одинаковы, а фазовые спектры отличаются на.

Спектр аналитического сигнала (2.5.2) согласно теореме о спектре суммы будет определяться выражением

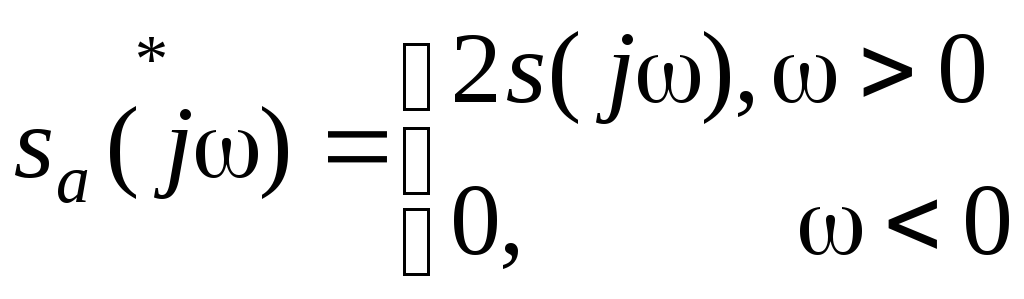(2.8.9)

т.е. будет ''односторонним''.

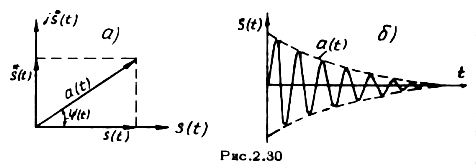
Аналитический сигнал можно представить в виде вектора на плоскости (рис.2.30) и записать в показательной форме:

(2.5.10)

(2.5.11)

(2.5.12)

При такой записи для действительного сигнала s(t) и сопряженного ему имеем

(2.5.13), (2.5.14)

Вследствие однозначности преобразования Гильберта функции иопределяются такжеоднозначно и называются огибающей и фазой действительного сигнала . Правомерность этих названий вытекает из следующих свойств аналитического сигнала:

1. , что следует из (2.5.11).

2. в тех точках, где, что следует из (2.5.12) и (2.5.13).

3. , если. Действительно, дифференцируя равенство (2.5.11), имеем

откуда с учетом второго свойства следует приведенное равенство. Следовательно, в точках, где , кривыеa(t) s(t) имеют общие касательные.

Таким образом, функции a(t) и s(t) нигде не пересекаются и только в точках, где , а, касаются друг друга, (рис.2.30 б). Это и позволяет функциииназывать огибающей и фазой сигнала.

Используя (2.5.12), можно дать общее определение круговой частоты колебания

(2.5.15)

Для радиосигналов, выделив из мгновенной частоты постоянную составляющую, равную , получим

(2.5.16)

Последняя запись справедлива для всех узкополосных сигналов. Поэтому для них можно записать

(2.5.17)

где функции ибудут медленно меняющимися функциями по сравнению с.

Для простых сигналов, составленных из небольшого числа гармонических колебаний, не представляет труда осуществить запись в виде огибающей и фазы, не прибегая к понятию аналитического сигнала. Однако, для более сложных сигналов, использующихся в системах связи, определить огибающую и фазу удается только при представлении сигнала в виде аналитического.

Заметим, что устройства тина амплитудного, фазового или частотного детектора позволяют выделить из сигнала его огибающую, фазу или частоту.

В качестве простого примера приведем запись АМ - сигнала в виде аналитического

(2.5.18)

Из этого выражения с использованием (2.5.13) получим

(2.5.19)

и

(2.5.20)