Глава II детерминированные сигналы

§ 2.1 Спектральное представление детерминированных сигналов

Как отмечалось в главе I, сигналы связи по своей природе являются случайными процессами. Однако, отдельные реализации случайного процесса и некоторые специальные (например, испытательные) сигналы можно считать детерминированными функциями. Последние принято делить на периодические, почти периодические и непериодические, хотя строго периодических сигналов в реальных условиях не существует.

Сигнал называется периодическим, если он удовлетворяет условию

(2.1.1)

на интервале , гдеТ – постоянная величина, называемая периодом, а к - любое целое число.

Непериодическим называется сигнал, который не удовлетворяет условию (2.1.1.) на всей оси времени. Он задается на конечном или полубесконечноминтервале времени, а за пределами этого интервала принимается тождественно равным нулю. Непериодический сигнал можно рассматривать как периодический, но с бесконечно большим периодом. Одной из характеристик непериодического сигнала является его длительность, под которой понимают либо длительность соответствующую всему сообщению или отрезку сообщения, либо длительность отдельного элемента (например, элемента кодовой комбинации).

Почти периодическим сигналом называется такой, для которого период можно указать лишь приближенно. Такими сигналами являются, например, сигналы, которые могут быть представлены в виде суммы гармонических составляющих с произвольными (не кратными) частотами.

В теории сигналов широко используется спектральное представление сигналов. Спектральным представлением детерминированного сигнала s(t) называется его представление в виде суммы конечного или бесконечного числа гармонических составляющих. Основой спектрального представления сигналов является преобразование Фурье. Рассмотрим сначала спектральное представление модулирующих или видеосигналов.

Как известно из математики, любую периодическую функцию с периодом Т, удовлетворяющую условиям Дирихле, можно представить в виде ряда Фурье

(2.1.2)

где а коэффициенты– определяются по формулам

(2.1.3)

Величина (2.1.4)

определяет среднее значение сигнала за период и называется постоянной составляющей. Частота называется основной частотой сигнала, а кратные ей частоты– высшими гармониками.

Выражение (2.1.2) можно переписать следующим образом

(2.1.5)

где (2.1.6)

Обратные зависимости для коэффициентов имеют вид

(2.1.7)

При форме записи (2.1.5) коэффициент выражает амплитуду, а- фазук-ой гармоники. Совокупность коэффициентов носит название спектра амплитуд, а совокупность значений - спектра фаз.

На рис.2.1 приведен график спектра амплитуд периодического сигнала. Аналогичный вид имеет и спектр фаз. Спектр периодической функции называется линейчатым или дискретным, так как состоит из отдельных линий, соответствующих частотам

Если функция s(t), описывающая сигнал, четная, т.е. то согласно (2.1.3) все , и соответствующий ей ряд Фурье будет содержать только косинусоидальные члены. Если функция s(t) - нечетная, т.е. , то в ряде Фурье будут только синусоидальные члены. С использованием выражения

вместо (2.1.5) можно записать

(2.1.8)

Согласно выражениям (2.1.3) и (2.1.6) коэффициенты ичетны относительнок, а коэффициенты и фазовые углы- нечетны, т.е.

(2.1.9)

Поэтому вторую сумму в (2.1.8) можно представить в следующем виде:

(2.1.10)

Объединяя обе суммы выражения (2.1.8), получим так называемую комплексную или показательную форму ряда Фурье

(2.1.11)

где коэффициенты называются комплексными амплитудами гармоник и связаны с коэффициентами и , а такжеисоотношениями

(2.1.12)

На основании выражений (2.1.12) и (2.1.3) можно также записать

(2.1.13)

Сравнивая (2.1.5) и (2.1.13), замечаем, что при использовании комплексной записи ряда Фурье отрицательные значения К позволяют говорить о составляющих с ''отрицательными'' частотами. Однако появление отрицательных частот имеет формальный характер и связано с использованием комплексной формы записи для представления действительного сигнала. В самом деле, гармонической составляющей с ''физической'' частотой в выражении (2.1.11) соответствует следующая пара слагаемых

Эта пара слагаемых, вследствие четности модуля и нечетности фазы , дает в сумме вещественную гармоническую функцию с положительной частотой:

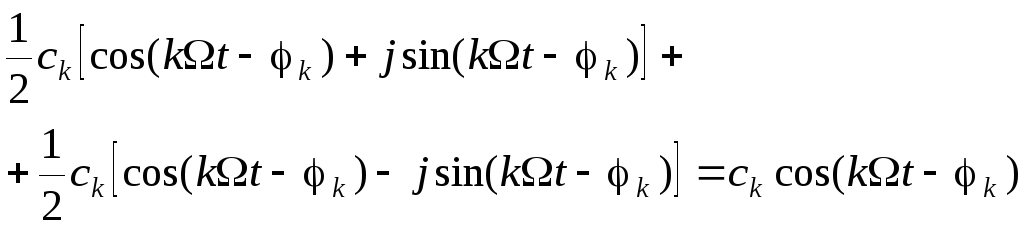(2.1.14)

Благодаря удвоению числа составляющих при использовании показательной формы записи ряда Фурье амплитуды их в 2 раза уменьшаются. Использование такой записи в значительной степени упрощает математические выкладки при исследовании прохождения сигналов через различные линейные системы.

Вычислим теперь среднюю за период мощность сигнала

(2.1.15)

где волнистая черта сверху означает усреднение по времени. Подставляя (2.1.2) в (2.1.15) и учитывая, что

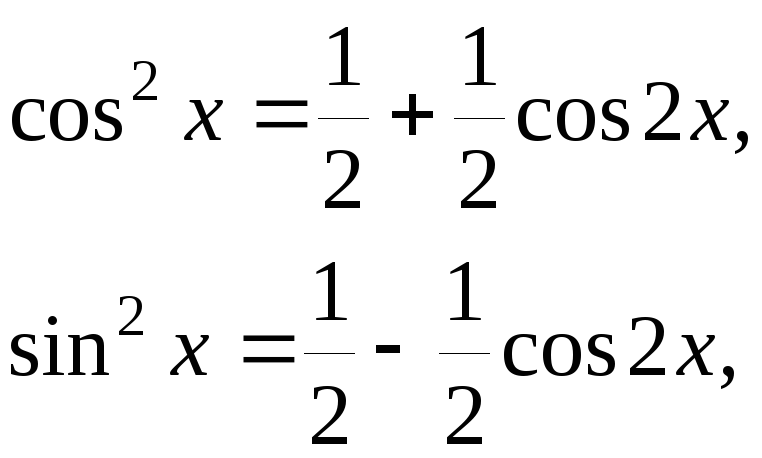
а интегрирование за период исходной функции Т гармонических колебаний с удвоенной частотой и произведений косинусов и синусов с аргументами неодинаковой кратности дает нуль, вместо (2.1.15) получим

(2.1.16)

Это выражение носит название равенства Парсеваля, которое показывает, что средняя мощность сигнала равна сумме средних мощностей его частотных составляющих и не зависит от фазовых соотношений между отдельными составляющими.

СПЕКТРЫ НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ

Разложение в ряд Фурье может быть обобщено и на случай непериодического сигнала. Действительно, пусть имеется периодический сигнал с периодомТ и определенными амплитудным и фазовым спектром (рис.2.2).

Если функция остается неизменной на интервале , то непериодическую функцию можно рассматривать как предельный случай периодической функции с неограниченно возрастающим периодом. При увеличении Т частота первой гармоники уменьшается и спектральные линии на рис.2.2 б располагаются чаще. В пределе, при, интервал между линиями в спектре сокращается до нуля, т.е. спектр вместо дискретного становится сплошным, непрерывным. Амплитуды гармоник, согласно (2.1.13), становятся бесконечно малыми. Математически это можно выразить следующим образом. Введем вместо (2.1.13) функцию

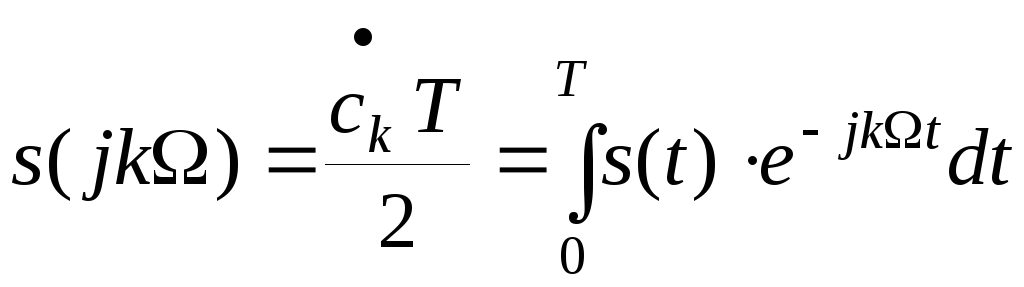(2.1.17)

Тогда вместо (2.1.11) получим

(2.1.18)

При частотаможет принимать любое значение ω,

Поэтому вместо (2.1.17) и (2.1.18) окончательно получим

(2.1.19)

(2.1.20)

Эти два выражения носят название пары преобразований Фурье, которая связывает между собой функцию времени s(t) и комплексную функцию частоты s(jω).

Физический смысл формулы (2.1.20) состоит в том, что непериодический сигнал s(t)имеет непрерывный спектр, т.е. представляется бесконечной суммой гармонических колебаний с бесконечно малыми комплексными амплитудами (ср.(2.1.11))

(2.1.21)

Функция 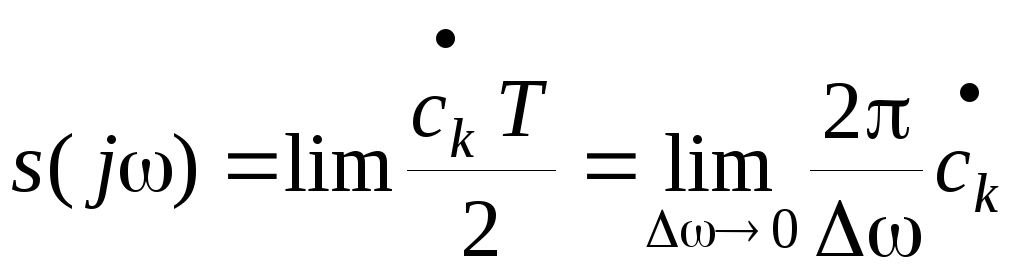имеет размерностьи показывает амплитуду сигнала, приходящуюся на единицу полосы частот в 1 Гц. Поэтому эта непрерывная функция частоты называетсяспектральной плотностью комплексных амплитуд или просто спектральной плотностью.

Аналогично (2.1.21) спектральную плотность комплексных амплитуд можно представить в виде

(2.1.22)

где и(2.1.23)

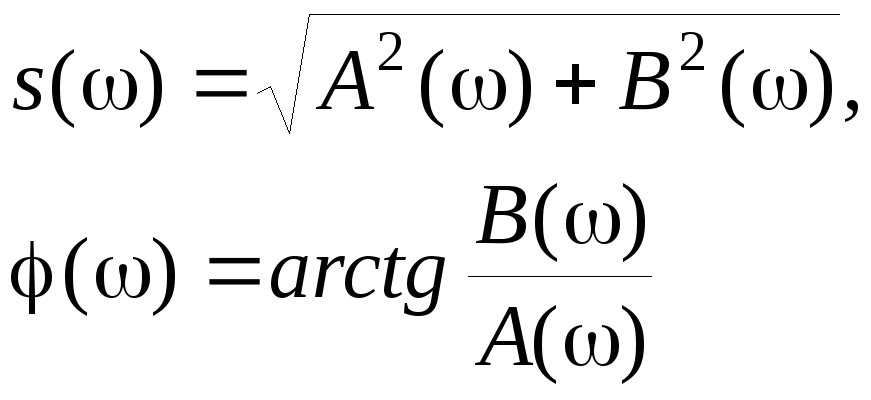(2.1.24)

Функция называется модулем спектральное плотности или спектральной плотностью амплитуд, а– спектральной плотностью фаз.

Отметим одно важное обстоятельство. Сравнивая выражения (2.1.13) и (2.1.17), замечаем, что при они отличаются только постоянным множителем, а

(2.1.26)

т.е. комплексные амплитуды периодической функции с периодом Т можно определять по спектральной характеристике непериодической функции такого же вида, заданной в интервале 0 - Т. Сказанное справедливо и по отношению к модулю спектральной плотности:

(2.1.26)

Это соотношение формулируется следующим образом: огибающая сплошного амплитудного спектра непериодической функции и огибающая амплитуд линейчатого спектра периодической функции совпадают по форме и отличаются только масштабом (рис .2.2)

Вычислим теперь энергию непериодического сигнала. Умножая обе части равенства (2.1.20) на s(t) и интегрируя в бесконечных пределах, получим

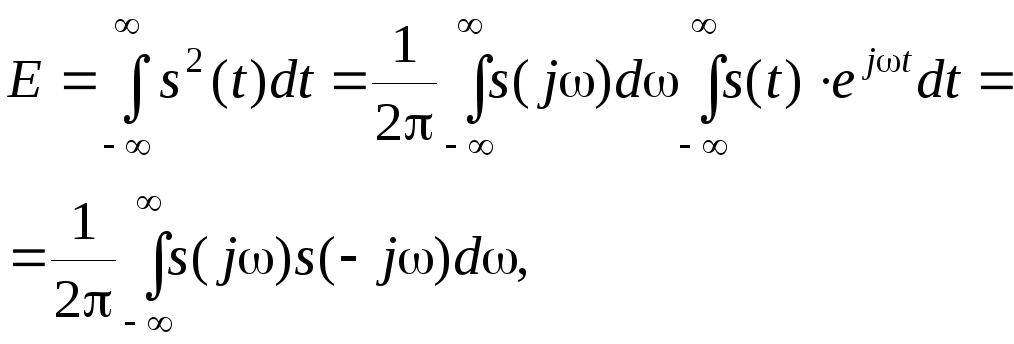(2.1.27)

где s(jω) и s(-jω) - комплексно-сопряженные величины. Так как

то

(2.1.28)

Это выражение называется равенством Парсеваля для непериодического сигнала и аналогично (2.1.16), однако в отличие от последнего оно определяет не среднюю мощность, а полную энергию сигнала.

Из (2.1.28) видно, что есть не что иное, как энергия сигнала, приходящаяся на 1Гц полосы частот около частоты ω.

Поэтому функцию иногда называют спектральной плотностью энергии сигналаs(t).

В заключение параграфа приведем без доказательства несколько теорем о спектрах, выражающих основные свойства преобразования Фурье.

1. Теорема сложения. Спектр суммы нескольких сигналов равен сумме спектров этих сигналов: (2.1.29)

В справедливости этого выражения легко убедиться, используя выражения (2.1.19) и (2.1.20).

2. Теорема запаздывания. Спектральная плотность сигнала, полученного при сдвиге сигналаs(t) по оси времени на , определяется выражением

т.е. сдвиг функции по оси времени приводит к появлению фазового сдвига для всех частотных составляющих, равного .

В справедливости последнего выражения легко убедиться, заменив в (2.1.19) t на .

3. Теорема смещения. Если - спектр функции s(t) то спектру - , полученному путем сдвига исходного спектра по оси частот на величину, соответствует функция

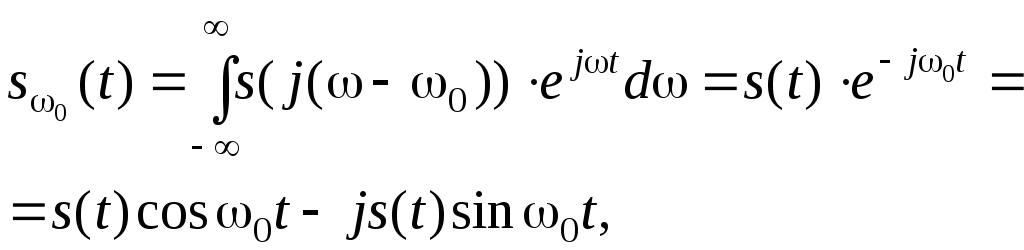(2.1.30)

4. Теорема о спектрах производной и интеграла. Спектры производной и интеграла от функции s(t) определяются соответственно выражениями

(2.1.31)

5. Теорема о спектре свертки. Сверткой двух функций иназывается интеграл

(2.1.32)

Спектр свертки двух функций равен произведению спектров свертываемых функций:

(2.1.33)

В частном случае, когда , то

(2.1.34)

Используя последнее выражение, легко получить ранее введенное равенство Парсеваля (2.1.28).