Контрольные вопросы

1. Что такое разрешенные и запрещенные зоны?

2. Что такое уровень Ферми?

3. Что такое собственный полупроводник?

4. Что такое диффузия и дрейф носителей заряда?

5. Что такое подвижность носителей заряда?

6. Как примеси влияют на характеристики полупроводника?

7. Что такое электронный и дырочный полупроводники?

8. Какова энергия Ферми в примесных полупроводниках?

9. Как объяснить температурную зависимость концентрации носителей заряда в полупроводниках?

10. Какими физическими факторами объясняется температурная зави­симость подвижности носителей заряда?

2. Контактные явления в полупроводниках

Электрическим переходом называют переходный слой в полупровод­ни­ко­вом материале между двумя областями с различными типами электро­про­вод­ности или разными значениями удельной электрической проводимости.

Если одна из контактирующих областей – металл, а другая – полупро­водник, то такой электрический переход называют переходом Шоттки. Если переход образован двумя полупроводниками с различной шириной запрещенной зоны, например германием и арсенидом галлия, его назы­вают гетеропереходом. Электрический переход, образованный в резуль­тате контакта полупроводников с одинаковой шириной запрещенной зоны, называют гомопереходом.

Электрический переход может быть выпрямляющим, т. е. иметь малое сопротивление при одном направлении тока и большое при другом. Электри­ческое сопротивление омических переходов в отличие от выпрям­ляющих не зависит от направления тока в заданном диапазоне его значе­ний. Большинство полупроводниковых приборов имеют выпрямляющие гомогенные электронно-дырочные (p–n) переходы.

Электронно-дырочный переход образуется между областями полупро­водника, одна из которых имеет электропроводность n-типа, а другая p-типа. По соотношению концентраций примесей в p- и n- областях разли­чают симметричные, несимметричные и односторонние переходы. Обычно в полупроводниковых приборах используют несимметричные переходы, у которых концентрации N_д и N_a различаются в несколько раз. Если концен­трации примесей различаются более чем в 10 раз, переход называют од­носторонним.

2.1. Электронно-дырочный переход в состоянии равновесия

В основе большинства полупроводниковых диодов и транзисторов ле­жит контакт двух полупроводников с различным типом электропроводнос­ти. Он может быть получен, например, путём диффузии донорной примеси в полупроводник p-типа. Идеализированная одномерная структура p-n-пе­рехода изображена на рис. 2.1, а.

Рассмотрим физические процессы в структуре, определяющие свой­ст­ва p-n-перехода.

Будем полагать, что концентрация легирующей примеси в областяхn- и p-типа распределена равномерно (рис. 2.1, б), причём концентрация до­норной примеси N_D в n-полупроводнике значительно больше, чем кон­цен­трация акцепторной примеси N_A в p-полупроводнике (N_D>>N_A). Назовём n-область с большей концентрацией примеси эмиттером, а p-область с меньшей концентрацией примеси – базой. Это допущение позволяет счи­тать, что полный ток через p-n-переход определяется пре­иму­щест­вен­но электронной составляющей. Дырочная со­ставляющая тока через p-n-переход ма­ла и ею можно пренебречь:

0. J = J_n + J_p J_n .

Будем полагать, что внешние выводы удалены от контакта на расстояние, зна­чи­тельно превышающее диффузионную дли­ну электронов L_n в базе и дырок L_p в эмит­тере. Это позволяет считать, что собст­вен­но p-n-переход локализован вблизи гра­ни­цы x_0. Обозначим границы p-n-перехода че­рез x_n и x_p.

Так как концентрация электронов в ­n-по­лупроводнике n_n (основные носители за­ря­да) значительно превышает кон­цен­тра­цию электронов в p-полупроводнике n_p (не­ос­новные носители заряда), то в плоскости контакта возникает диффузия электронов из n-области в p-область. Аналогичные рас­суждения объясняют диффузию дырок из p-области в n-область. Таким образом че­рез p-n-переход протекают диф­фу­зи­он­ные токи J_{n диф} и J_{p диф} , ( см. рис. 2.1, в) .

Свободные электроны, переходя в p-по­лупроводник, становятся там неосновными носителями и рекомбинируют с дырками. Одновременно в n-полупроводнике происходит рекомбинация переходящих туда дырок. В ре­зультате рекомбинации на границе p- и n-областей возникает обедненный носителями слой, концентрации свободных электронов и дырок в котором близки к нулю. Этот слой называют запирающим. Толщина запирающего слоя определяется длиной свободного про­бега электронов и дырок до их рекомбинации. При увеличении числа носителей длина их свободного пробега уменьшается, и обедненный слой становится тоньше. Следова­тельно, в несимметричномp-n-переходе обедненный слой имеет большую толщину в области полупроводника, где меньше концентрация примеси (в рассматриваемом примере – в p-по­лу­проводнике (рис. 2.1, б).

При уходе электронов из n-области в обедненном слое остаются поло­жительные заряды неподвижных ионов донорной примеси, ранее компен­сировавшиеся зарядами электронов. Аналогично p-полупроводник обед­няется дырками, и вблизи его границы возникает слой нескомпенсиро­ванных отрицательных ионов акцепторной примеси. Противоположные по знаку заряды ионов примеси создают в обедненном слое электрическое поле с напряженностью Е_к и контактной разностью потенциалов _к (рис. 2.1, в). Это электрическое поле, которое называют диффузионным, огра­ничено лишь областью перехода, совпадающей с границами запирающего обедненного слоя. В целом p-n-переход, электрически нейтрален. Энерге­тическая диаграмма перехода приведена на рис. 2.1, г.

Положительные заряды доноров и отрицательные заряды акцепторов в запирающем слое уравновешивают друг друга.

Электрическое поле p-n-перехода направлено так, что препятствует дальнейшей диффузии основных носителей, но ускоряет неосновные но­сители, возникающие в запирающем слое. Они легко перемещаются через обедненный слой, создавая дрейфовые токи дырок из n-полупроводника в p-область, электронов из p-полупроводника в n-полупроводник. Направле­ния дрейфовых токов противоположны направлениям диффузионных то­ков. По мере формирования p-n-перехода диффузионные токи уменьша­ются, а дрейфовые – возрастают, пока не уравновесят друг друга.

При равновесном состоянии p-n-перехода его результирующий ток ра­вен нулю, однако при этом происходят перемещения носителей через пе­реход.

Свойства p-n-перехода характеризуют два основных параметра: кон­тактная разность потенциалов _k и толщина запирающего слоя . Найдем соотношения, определяющие зависимости этих параметров от темпера­туры, концентрации примесей и материала полупроводника.

Контактную разность потенциалов можно определить из условия ра­венства нулю суммарных электронных или дырочных токов при равновес­ном состоянии p-n-перехода.

j_{диф n} = – j_{дрейф n} , т. е. D_n = – n_p , (2.1)

но E_к= – d / dx, тогда

D_n = n_p d / dx . (2.2)

Разделим на n_p и проинтегрируем в пределах толщины запирающего слоя p-n-перехода:

D_n = 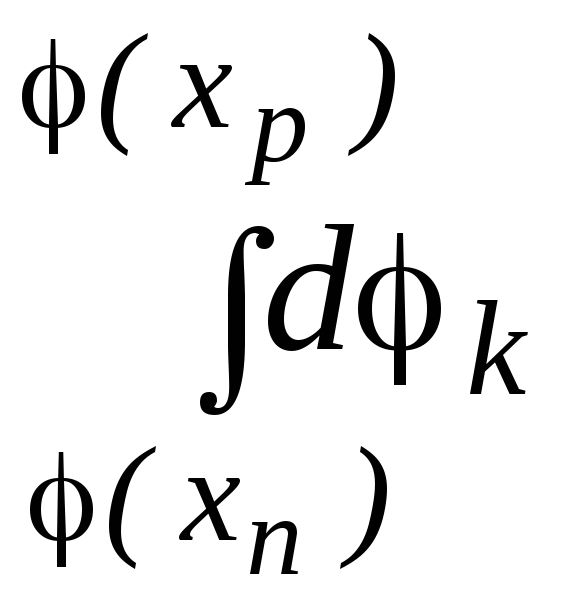. (2.3)

Заменяя переменные n(x_p) = n_p, n(x_n) = n_n, (x_p) = _p, (x_n) = _n и интегри­руя, получим:

D_n(ln n_p – ln n_n) = (_p – _n). (2.4)

Используя соотношение Эйнштейна, определим контактную разность потенциалов:

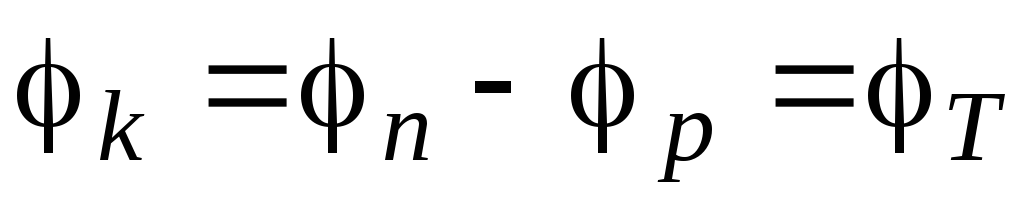0. ln. (2.5)

Для расчёта ширины перехода и закона распределения электриче­ского потенциала в переходе (см. рис. 2.1, в) принимают, что в области пе­рехода подвижные носители заряда отсутствуют полностью (объёмные заряды определяются ионами акцепторной и донорной примеси). Тогда используя уравнение Пуассона [1] , можно получить

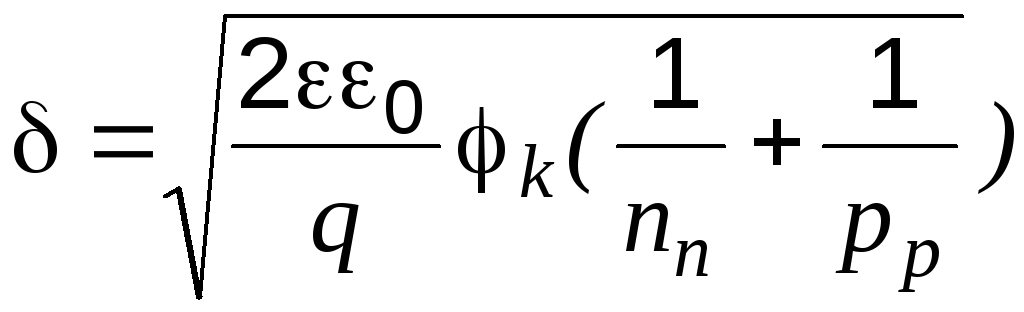0. . (2.6)

Анализ выражений (2.5) и (2.6), показывает, что параметры перехода зависят от температуры и концентрации легирующей примеси в n- и p-об­лас­тях.

Увеличение температуры приводит к уменьшению контактной разности потенциалов и шириныp-n-перехода . Это, в первую очередь, опреде­ляется тем, что, как показано в разд.1, при высоких температурах уровни Ферми вn- и p-полупроводниках приближаются к середине запре­щенной зоны, электропроводность полупроводников стремится к собст­венной, а, следовательно, p-n-переход исчезает (,).

При возрастании концентрации легирующих примесей N_D и N_A контакт­ная разность потенциалов возрастает, а ширина p-n-перехода уменьша­ется.

Необходимо отметить, что область p-n-перехода обеднена подвиж­ными носителями заряда, так как любой, возникший в этой области или попавший в неё, подвижный заряд выталкивается из области перехода электрическим полем. Поэтому сопротивление p-n-перехода значительно выше, чем сопротивление n- и p-областей.