5. Точки разрыва функции
Напомним, что точка является точкой непрерывности функции , если выполняются три условия:
1) функция определена в точке ;
2) существует предел
;
3) имеет место
равенство
.
Если не выполняется хотя бы одно из этих трех условий, то точка не является точкой непрерывности функции . Таким образом, можно определить новое понятие. Точка называется точкой разрыва функции , если имеет место хотя бы одно из следующих условий:
1) функция не определена в точке ;
2) не существует предел ;
3) выполняется
неравенство
.
Пример 1.
Точка
является точкой разрыва функции
;
точка
не принадлежит области определения
этой функции и
.
Пример 2.
Точка
является точкой разрыва функции
;
хотя точка
принадлежит области определения функции,
однако в этой точке не существует предел:
.
Пример 3.
Точка
является точкой разрыва функции
;
хотя в точке
существует предел
,
однако сама функция не определена в
этой точке.
Пример 4.
Точка
является точкой разрыва функции
;
хотя точка
принадлежит области определения функции
и в этой точке существует предел
,
однако не выполняется равенство
,
так как
,
но
.
6. Классификация точек разрыва функции
Пусть
является точкой разрыва функции
и пусть в этой точке существуют конечные
пределы
и
.
Если выполнено хотя бы одно из условий:
1)
;
2)
;
3)
и
;
4)
и
,
то точка разрыва
называется точкой
разрыва I
рода функции
.
Если
является точкой разрыва I
рода функции
,
но выполняется равенство
,
то точка
называется устранимой
точкой разрыва
функции
.
Устранимую точку разрыва
функции
можно превратить в точку непрерывности
этой функции, доопределяя функцию в
этой точке, если
и, переопределяя – если
,
полагая, в обоих случаях,
.
Если – точка разрыва, но не является точкой разрыва I рода функции , то она называется точкой разрыва II рода функции .
Точка разрыва является:
точкой разрыва II рода для функции в примере 1;
точкой разрыва I рода для функции в примере 2; но не является устранимой точкой разрыв;
устранимой точкой разрыва для функции в примере 3;
устранимой точкой разрыва для функции в примере 4.
7. Обращение непрерывной функции в нуль
Отметим некоторые свойства функций, непрерывных на отрезке.
Теорема 2. (Первая
теорема Больцано – Коши).
Пусть функция
определена и непрерывна на отрезке
и на концах отрезка принимает значения
разных знаков. Тогда между точками
и
найдется хотя бы одна точка
,
в которой функция обращается в нуль.
Приведенная теорема
имеет простой геометрический смысл.
График непрерывной функции
,
соединяющий точки
и
,
где
,
(рис. 1) и
,
(рис. 2), хотя бы один раз пересекает ось
абсцисс.
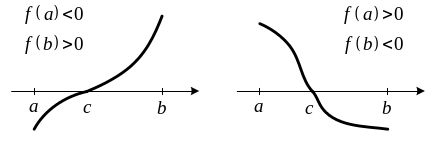
Рис. 1 Рис. 2
Первая теорема Больцано – Коши имеет многочисленное приложение. Например, ее можно использовать для доказательства существования решения уравнений.
Пример
1. Докажем,
что уравнение
имеет хотя бы один корень на отрезке
.
Действительно,
функция
является непрерывной на отрезке
и на концах данного отрезка принимает
значения:
– противоположных знаков. Поэтому, по
первой теореме Больцано – Коши найдется
точка
такая, что
.
Это означает, что
является корнем данного уравнения:
.