2. Непрерывность простейших элементарных функций
Простейшие элементарные функции – степенные, показательные, логарифмические, тригонометрические и обратные тригонометрические функции, являются непрерывными во всех точках своих областях определений.
2.1. Непрерывность
степенной функции.
Функция
непрерывна в произвольной точке
.
(Областью определения функции
,
в зависимости от значения
,
может являться один из трех промежутков:
,
или
.)
Действительно, если
,
то
,
и
при
;
если
,
то
при
.
2.2. Непрерывность
показательной функции.
Функция
непрерывна в произвольной точке
.
Действительно, так как
,
то
при
.
2.3. Непрерывность
логарифмической функции.
Функция
непрерывна в произвольной точке
.
Действительно,
при
.
2.4. Непрерывность
тригонометрической функции синус.
Функция
непрерывна в произвольной точке
.
Действительно, из тождества
,
(1)
получим
.
Так как
и
– ограниченная величина, то
при
.
2.5. Непрерывность
тригонометрической функции косинус.
Функция
непрерывна в произвольной точке
.
Действительно, из тождества
,
(2)
получим
.
Так как
и
– ограниченная величина, то
при
.
2.6. Непрерывность
тригонометрической функции тангенс.
Функция
непрерывна в произвольной точке
.
Действительно, из тождества
,
получим
.
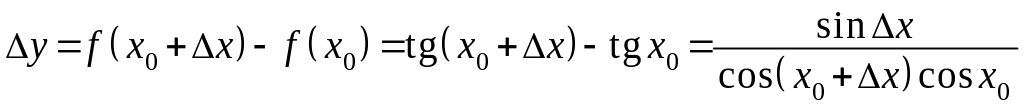Так как
и
– ограниченная величина, то
при
.
Отсюда и из периодичности функции вытекает ее непрерывность во всех точках области определения.
2.7. Непрерывность
тригонометрической функции котангенс.
Функция
непрерывна в произвольной точке
.
Действительно, из тождества
,
получим
.
Так как
и
– ограниченная величина, то
при
.
Отсюда и из периодичности функции вытекает ее непрерывность во всех точках области определения.
Непрерывность обратных тригонометрических функций будет доказана ниже.
3. Арифметические операции
над непрерывными функциями
Теорема 1.
Пусть функции
и
непрерывны в точке
.
Тогда их сумма
является непрерывной функцией в точке
.
Теорема 1 имеет место для любого конечного числа слагаемых.
Теорема 2.
Пусть функции
и
непрерывны в точке
.
Тогда их разность
является непрерывной функцией в точке
.
Теорема 3.
Пусть функции
и
непрерывны в точке
.
Тогда их произведение
является непрерывной функцией в точке
.
Теорема 4.
Пусть функции
и
непрерывны в точке
.
и
.
Тогда их частное
является непрерывной функцией в точке
.
Эти теоремы позволяют исследовать на непрерывность сложные функции, расчленяя их на более простые функции.
4. Суперпозиция непрерывных функций
Более широкие классы непрерывных функций можно построить с помощью суперпозиции функций, непрерывность которых уже установлены.
Теорема
1. Пусть
функция
определена в промежутке
,
а функция
– в промежутке
,
причем область значений
функции
целиком содержится в промежутке
.
Если функция
непрерывна в точке
,
а функция
непрерывна в соответствующей точке
,
то сложная функция
будет непрерывна в точке
.