Тема 2. Загальна лінійна економетрична модель. Методи побудови та дослідження план (логіка)викладу і засвоєння матеріалу

2.1.Постановка та основні означення парної лінійної регресії. Метод найменших квадратів. Система оцінки параметрів економетричної моделі з двома змінними.

2.2.Дисперсійний та кореляційний аналіз побудованої моделі.

2.3.Постановка загальної лінійної моделі.

2.4.Передумови застосування методу найменших квадратів (1МНК).

2.5.Властивості оцінок параметрів.

2.6. Перевірка моделі на якість і точність.Прогноз.

2.1. Постановка та основні означення парної лінійної регресії. Метод найменших квадратів. Система оцінки параметрів економетричної моделі з двома змінними.

На базі простої економетрічної моделі розглянемо принципову структуру економетрічної моделі та основні методи оцінювання її параметрів.

Найпростішою є лінійна форма зв’язку між двома змінними:

(2.1)

де і _– невідомі параметри.

Щоб розв’язати цю задачу до економетричної моделі вводять стохастичну складову, яка акумулює в собі всі відхилення фактичних спостережень змінної У від обчислених в моделі, тоді загальна форма економетричної лінійної моделі має вигляд:

(2.2)

Введення в модель стохастичної складової, яку ще називають похибкою, збуренням, відхиленням, зумовлена слідуючи ми факторами:

1. На величину У впливають ще інші об’єктивні чинники.

2. На величину Х також впливають випадкові фактори.

3. Крім того існує ймовірність помилки вимірювання.

Ця випадкова змінна в економетричній моделі має математичний розподіл нуль, дисперсію . Тому на підставі центральної граничної теореми стохастична складова економетричної моделі розподілена за нормальним законом.

Парна лінійна регресія (У на Х) називається двохстороння стохастична лінійна залежність між випадковими величинами (показник У і фактор Х), які знаходяться в причинно-наслідкових відношеннях, причому зміна фактора викликає зміну показника.

Слід відрізняти стохастичну залежність від функціональної. При цьому одному значенню фактора може відповідати декілька значень попередника.

Суть регресійного аналізу полягає в тому, щоб знайти згладжувальну лінію, яка найкращим чином проходить через задану множину точок (Х,У).

Найпоширеним методом при розв’язанні подібних проблем є метод найменших квадратів МНК ( основоположники К. Гаус, П. Лаплас).

Справжні значення параметрів обчислити не можна , тому здобуті значення параметрів лінійної моделі є статистичними оцінками справжніх параметрів а і b.

Розглянемо різницю у та , де у – фактичні, - розрахункові значення показника. U= у - .

МНК для парної лінійної регресії полягає в підборі таких оцінок параметрів регресії та для яких сума квадратів відхилень спостережуваних даних показника від зглажувальних буде мінімальною, тобто:

U²=(у - )²= min (2.3)

Необхідною умовою існування мінімуму функціонала U² є рівність нулю частинних похідних цього функціоналу по і . А достатньою умовою існування екстремуму в критичній точці ( ; ) є додатне значення визначника складеного з частинних похідних другого порядку.

Принцип найменших квадратів відхилень полягає в знаходженні таких і , для яких найменша. Необхідна умова для цього — перетворення на нуль похідних цієї функції за кожним із параметрів і . Метод, який реалізує принцип найменших квадратів, називається методом найменших квадратів (1МНК). Оскільки

,

то

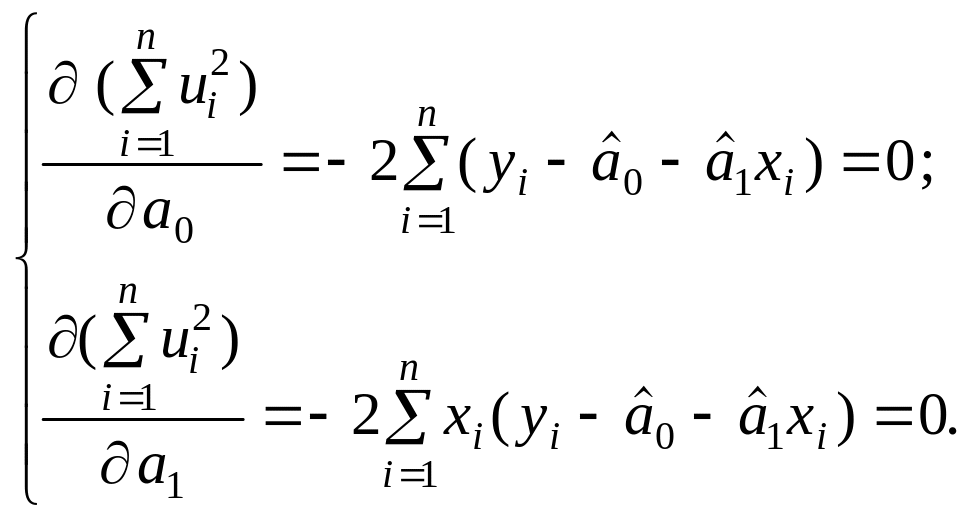
Виконавши елементарні перетворення, дістанемо систему нормальних рівнянь

(2.4)

Підставимо в систему (2.4) значення , , , , які можна дістати на підставі сукупності спостережень, і розв’яжемо її відносно невідомих параметрів і :

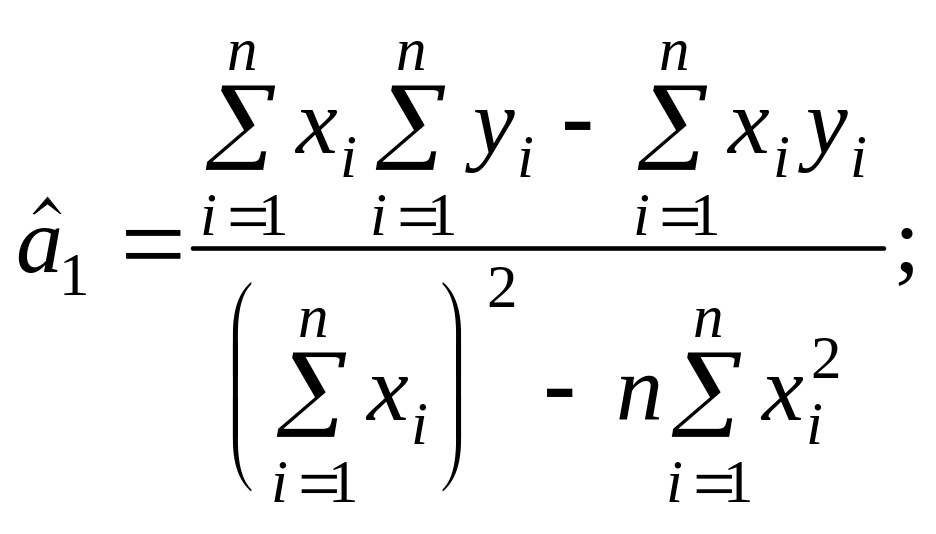
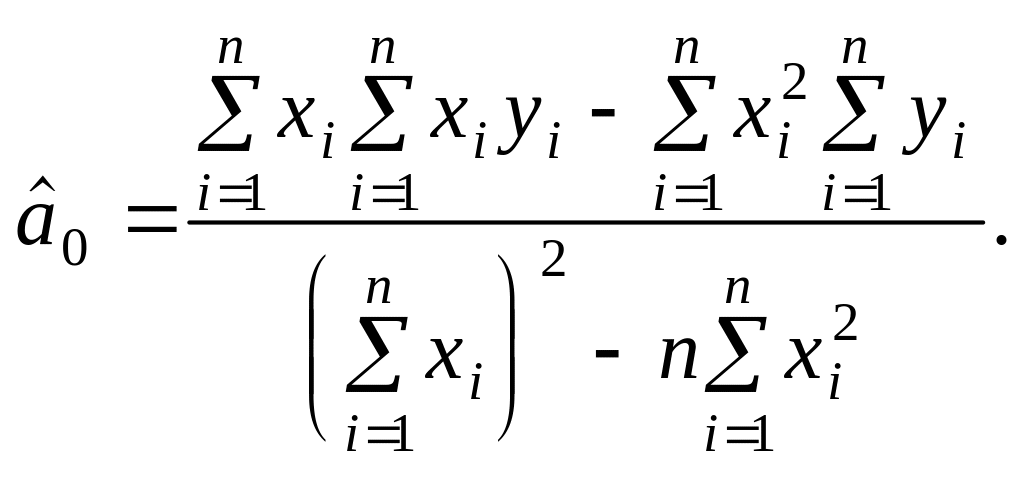
Оскільки оцінки найменших квадратів такі, що лінія регресії обов’яз­ково проходить через точку середніх значень ( ), то оцінки параметрів моделі можна знайти дещо інакше.

Поділивши перше рівняння системи (2.4) на n, дістанемо:

. (2.5)

Віднімемо (2.2) від (2.1):

.

Нехай

, і ,

тоді

,

а відхилення фактичних значень від розрахункових будуть такі:

.

Сума квадратів залишків при цьому,

.

Мінімізація цієї суми за невідомим параметром дає співвідношення:

. (2.6)

Крім того, можна помітити, що тобто друга похідна за параметром від суми квадратів відхилень додатна. Отже, знайдене значення відповідає мінімуму суми квадратів відхилень.

Якщо чисельник і знаменник виразу ( ) поділити на ( ), то після нескладних перетворювань отримаємо:

(2.7)

Зауважимо, що оцінки параметрів моделі згідно з методом МНК є досить чутливими до точності розрахунків.

Параметр можна обчислити, використавши співвідношення (2.5):

. (2.8)

Співвідношення (2.8) можна було б дістати також, записавши друге рівняння системи (2.4) через відхилення кожної змінної від її середнього арифметичного значення, згадавши при цьому, що сума таких відхилень завжди дорівнює нулю.