Унитарные и Евклидовы пространства.

Опр.: Говорят, что на задано скалярное произведение, если каждое поле векторов однозначно поставлено в соответствие число . И при этом выполняются следующие аксиомы : 1) ; 2) ; 3) ; 4) при ).

Опр.: ! на задано скалярное произведение. Если , то называется евклидовым (унитарным) пространством.

Опр.: Длиной (нормой) вектора называется неотрицательное действительное число .

Теорема (неравенство Коши-Бунековского): Для векторов 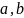унитарного пространства выполняется неравенство .

Доказательство: По аксиоме 4 . Если , то неравенство очевидно. ! . Полагаем . Получим . Умножая это неравенство на получим .

Опр.: Углом между ненулевыми векторами унитарного пространства называется угол, определяемый из условия .

Опр.: Векторы унитарного пространства называются ортогональными, если

Лемма: Если –ненулевые взаимно ортогональные векторы, то они линейно независимые.

Доказательство: ! . Тогда по аксиоме 4 система линейно независима по определению.

Опр.: Система векторов называется ортонормированной, если при и .

Теорема: Каждая ортонормированная система ненулевых векторов может быть дополнена до ортонормированной базы пространства .

Следствие : Пространство обладает ортонормированной базой. Действительно, если , то 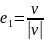– единичный вектор. Для системы применяем теорему.

Доказательство: Рассмотрим вектор , где –линейная оболочка векторов . По лемме – линейно независимые 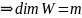. Тогда – линейно независимая система. Рассмотрим вектор . Очевидно, (иначе ). Подберем таким образом, чтобы . Для этого необходимо: . Итак, при найденных вектор ортогонален всем векторам Полагаем , тогда –ортонормированная система векторов. Продолжая эти рассуждения мы построимортонормированную базу пространства .

Теорема: ! – база унитарного пространства , 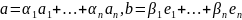. Данная база ортонормированная .

Доказательство: ! – ортонормированная база.Тогда , т.к. . ! есв. равенства . Тогда –ортонормированная база.

Ортогональные суммы.

Опр.: Подпространства и называются ортогональными, если .

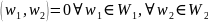Опр.: Сумма подпространств называется ортогональной, если при .

Лемма: Ортогональная сумма подпространств является прямой.

Доказательство: ! , где . В силу замечания из пункта «Прямые произведения» достаточно показать, что . Действительно, . По аксиоме 4 скалярного произведения .

Ортогональное дополнение.

Опр.: ! подпространство унитарного пространства . Множество Это ортогональное дополнение подпространства . Очевидно, что - подпространство пространства .

Теорема: .

Доказательство: ! – это ортонормированная база . По теореме из предыдущего пункта такие векторы –ортонормированная база пространства . ! – линейная оболочка векторов . Очевидно, что и при этом . Остаётся доказать, что . ! . В силу , где . Мы имеем , т.е. . Итак, .