Собственные векторы.

Опр.: Ненулевой вектор называется собственным вектором преобразования , если –собственное значение преобразования . Говорят, что собственный вектор принадлежит собственному значению .

Лемма: Если – собственный вектор преобразования с собственным значением , то –собственный вектор с собственным значением .

Доказательство: .

Опр.: ! – квадратная матрица порядка с коэффициентами из поля , – некоторая неизвестная (буква), –единичная матрица порядка . Матрица называется характеристической для матрицы . называется характеристическим многочленом матрицы , его корни называются характеристичными корнями, называется характеристическим уравнением матрицы .

Опр.: Матрицы и называются подобными (сопряжёнными), если .

Лемма: Подобные матрицы обладают одинаковыми характеристическими многочленами.

Доказательство: Действительно, .

Опр.: ! – база пространства , –это матрица преобразования в данной базе.

Опр.: Характеристическим многочленом (уравнением, корнем) преобразования называется характеристический многочлен (уравнение, корень) матрицы .

Лемма (критерий диагольнальности матрицы линейного преобразования): ! – матрица линейного преобразования в некоторой базе , –диагональная матрица .

Доказательство: – диагональная. Аналогично.

Инвариантные подпространства.

Опр.: Подпространство пространства называется инвариантным относительно ( -инвариантным), если .

Предложение: Если – -инвариантное подпространство, то – -инвариантное подпространство.

Доказательство: .

Многочленные матрицы.

Опр.: Рассмотрим квадратную матрицу -го порядка 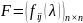, где . Матрицы такого вида называются многочленными (или -матрицы).

Опр.: Элементарными преобразованиями строк (столбцов) матрицы называются следующие преобразования: 1) Умножение строки (столбца) матрицы на ненулевой элемент ; 2) Перестановка двух строк (столбцов); 3) Прибавление к одной из строк (столбцов) другой строки (столбца), умноженной на многочлен .

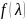Лемма 1: ! – элементарное преобразование. Тогда – тождественное преобразование.

Опр.: Говорят, что – матрица -эквивалентна. – матрице , если . Запись .

Лемма 2: Отношение эквивалентности обладает следующими свойствами: 1) (рефлексивность); 2) (симметричность); 3) (транзитивность).

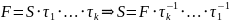Доказательство: 1) т.к. ; 2) ; 3) .

Следствия: Множество всех квадратных -матриц порядка разбиваются на непересекающиеся классы эквивалентных между собой -матриц. – класс эквивалентных - матриц, содержащий фиксированную матрицу .

Опр.: -матрица вида называется канонической диагональной, если –унитарные многочлены (старший коэффициент равен ) и .

Теорема 1: -матрица цепочкой элементарных преобразований приводится к каноническому диагональному виду (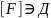 – канонические диагональные матрицы).

Доказательство: Индукция по . Если – нулевая матрица, то она уже каноническая диагональная. ! . Из всех матриц класса выберем матрицу , у которой и если , то . Очевидно, можно считать, что – это унитарный многочлен. ! . Разделим каждый многочлен на с остатком: . Обозначим : умножение 1-го столбца на 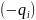и прибавление этого к -му столбцу; –это перестановка 1-го и -го столбцов. Тогда (в силу выбора матрицы ). Отсюда выводим следующее: содержит матрицу . Рассуждая аналогично, получим, что . По индуктивному предположению элементарными преобразованиями строк и столбцов с номерами 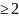матрицу можно привести к виду , где –унитарный многочлен и . Остаётся доказать, что . Действительно, умножим вторую строку на 1 и прибавим к 1-й. Получим, что в . Аналогично вышеизложенному доказываем, что – каноническая диагональная матрица.

Опр.: ! – квадратная -матрица порядка . Обозначим 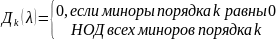. Будем считать, что если , то это унитарный многочлен.

Теорема 2: Многочлены не изменяются при элементарном преобразовании матрицы .

Доказательство следует из свойств определителей.

Опр.: ! , где на главной диагонали . Многочлены называются инвариантными множителями матрицы .

Теорема 3: ! отличны от нуля, , . Тогда .

Следствие: приводится элементарными преобразованиями к каноническому диагональному виду (инвариантные множители определяются матрицей однозначно).

Доказательство: В силу теоремы 2 многочлены для матриц и совпадают. Поскольку , то . Пусть . минор порядка матрицы . Тогда либо имеет ненулевую строку, столбец, либо имеет вид . Поскольку имеет минор порядка и при этом ) и т.д.

Теорема (признак эквивалентности -матриц в терминах инвариантных множителей): Две квадратные -матрицы порядка эквивалентны они обладают одинаковыми наборами инвариантных множителей.

Доказательство: ! и обладают одинаковыми наборами многочленов и обладают одинаковыми наборами инвариантных множителей. ! и обладают одинаковыми наборами инвариантных множителей. – каноническая диагональная матрица, тоже для 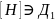. По нашему предположению .

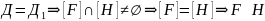Теорема (матричный признак эквивалентности): ! – квадратные -матрицы порядка . , где –ненулевые элементы поля.

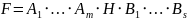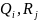Доказательство: ! . В силу замечания , где –матрицы вида из замечания и и –ненулевые элементы поля. Значит, если , то - ненулевые элементы поля. – ненулевые элементы поля – искомые матрицы. ! теперь , где и –элементы поля. Заметим, что многочлен матрицы равен . Отсюда , т.к. – унитарные многочлены. Значит, (признак эквивалентности -матриц в терминах инвариантных множителей). По замечанию , где –матрицы типа из замечания. Аналогично, , где –матрицы типа из замечания, т.о. . Снова по замечанию .