Линейные преобразования.

Опр.: Отображение называется линейным преобразованием пространства , если 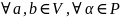1) ; 2) .

Теорема (о характеризации линейного преобразования действием на базе): ! – база линейного преобразования . – произвольный набор векторов из . Тогда линейное преобразование .

Доказательство: Каждый вектор пространства однозначно представим в виде . Полагаем 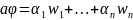, т.к. , то . Покажем, что – линейное преобразование. Если , то по определению . Аналогично . ! – линейное преобразование и при это . Тогда , т.е. .

Введение: ! – координатная база пространства и –линейное преобразование . ! .

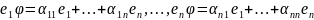Опр.: Матрица называется матрицей линейного преобразования в базе .

Лемма: Если – это координатная строчка вектора , то .

Доказательство: ! , т.е. .

Опр.: ! дана ещё одна координатная база пространства . Если , то называется матрицей перехода от первой координатной базы ко второй. Отметим, что – матрица линейного преобразования , для которого . гусь будем обозначать координатную строку вектора 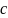в базе .

Теорема: ! – матрица линейного преобразования в базе . Тогда .

Доказательство: В силу леммы и по правилу преобразования координат .

Ранг и дефект линейного преобразования.

Опр.: ! – линейное пространство над полем , – линейное преобразование . непустого подмножества из полагаем – образ множества . – это прообраз .

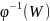Лемма: Если – подпространство из , то и – подпространство пространства .

Доказательство: Установим, например, что – подпространство. Действительно, , т.к. . Далее, .

Опр.: Ядром линейного преобразования называется множество .

Опр.: Рангом преобразования называется число

Опр.: Дефектом преобразования называется число .

Теорема (о сумме ранга и дефекта): .

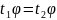Доказательство: По теореме о прямого дополнения Поэтому надо доказать, что . мы имеем . Предположим, что . Тогда – это критерий прямой суммы – взаимно однозначное отображение на , т.е. – изоморфизм на .

Действия с линейными преобразованиями.

Введение: ! – линейное пространство над полем , –линейное преобразование пространства , . Определим отображение из в .

Опр.: ! – произвольный вектор из . .

Лемма: – это те же линейные преобразования пространства .

Доказательство: Докажем, например, что –линейное преобразование. 1) ; 2) –линейное преобразование.

Теорема: Фиксируем базу пространства и через будем обозначать матрицу преобразования (произвольного) в данной базе. .

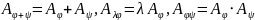Доказательство: Установим, например, равенство . ! – произвольный вектор пространства , – координатная строка в данной базе. Нам известно, что . Теперь по лемме из пункта «Координаты» .

Опр.: ! – кольцо и одновременно линейное пространство над полем . Если при этом выполняются равенства следующие , то называется алгеброй над полем .

Замечание: ! – линейное преобразование , –матрица преобразования в данной базе, тогда есть взаимно однозначное отображение множества всех линейных пространств на множество и при этом в силу предыдущей теоремы действие с линейными преобразованиями подчиняются тем же свойствам, что и действия с матрицами, поэтому множество всех линейных преобразований есть алгебра, изоморфная .