
- •Линейная алгебра. Линейное пространство.
- •Линейная зависимость. База. Размерность.
- •Изоморфизм.
- •Координаты.
- •Подпространства.
- •Ранг матрицы.
- •Общая теория линейных систем.
- •Однородное линейное уравнение.
- •Линейные преобразования.
- •Ранг и дефект линейного преобразования.
- •Действия с линейными преобразованиями.
- •Собственные векторы.
- •Инвариантные подпространства.
- •Многочленные матрицы.
- •Элементарные делители.
- •Нормальная форма Жордана.
- •Унитарные и Евклидовы пространства.
- •Ортогональные суммы.
- •Ортогональное дополнение.
Изоморфизм.
Опр.:
! – линейные пространства над полем
.
Тогда эти пространства называются
изоморфными, если
такие
взаимно-однозначные отображения
– линейные пространства над полем
.
Тогда эти пространства называются
изоморфными, если
такие
взаимно-однозначные отображения
 и
при этом 1)
и
при этом 1)
 ;
2)
;
2)
 .
.
 называется
изоморфизмом
на
называется
изоморфизмом
на
 .
Если
.
Если
 ,
то
называется
автоморфизмом пространства
.
,
то
называется
автоморфизмом пространства
.
Лемма
1: !
– нулевой элемент
,
 –нулевой
элемент
,
–изоморфизм
на
.
–нулевой
элемент
,
–изоморфизм
на
.
 .
.
Доказательство:
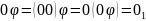 .
.
Лемма
2: Если
–система
образующих пространства, то
 –
линейно независимы.
–
линейно независимы.
Доказательство:
! напротив
 –линейно
зависимы. Тогда
–линейно
зависимы. Тогда
 ,
где хотя бы одно
,
где хотя бы одно
 и
при этом
и
при этом
 .
По условию
.
По условию
 .
Но тогда
.
Но тогда
 и
и
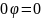 – это противоречие взаимной однозначности
отображения
.
– это противоречие взаимной однозначности
отображения
.
Теорема:
Линейные пространства
изоморфны
 .
.
Доказательство:
!
изоморфны,
–изоморфизм.
Если
– база
,
то в силу лемм 1, 2
 –база
.
Отсюда
–база
.
Отсюда
 .
!
.
!
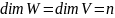 .
– база
,
.
– база
,
 – база
.
!
– база
.
!
 .
Тогда вектор
.
Тогда вектор
 однозначно
по замечанию записывается в виде
однозначно
по замечанию записывается в виде
 .
Полагаем, что
.
Полагаем, что
 .
Очевидно,
однозначно
отображает
на
.
Далее, если
.
Очевидно,
однозначно
отображает
на
.
Далее, если
 и
и
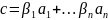 ,
то
,
то
 ,
,
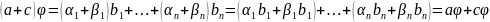 .
!
.
!
 ,
тогда
,
тогда
 и
и
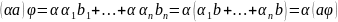 .
.
Координаты.
Опр.:
!
– линейное пространство над полем
,
 .
Координатной системой (базой) пространства
называется
база
.
Координатной системой (базой) пространства
называется
база
 ,
элементы которой рассматриваются в
определенном фиксированном порядке.
элемент
однозначно
записывается в виде
.
Элементы
,
элементы которой рассматриваются в
определенном фиксированном порядке.
элемент
однозначно
записывается в виде
.
Элементы
 называют
координатами вектора
в
базе
.
называют
координатами вектора
в
базе
.
 –
координатная строка вектора
в
.
–
координатная строка вектора
в
.
Опр.:
! задана ещё одна координатная база
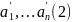 пространства
.
Мы имеем
пространства
.
Мы имеем
 .
Матрица
.
Матрица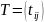 называется
матрицей перехода от координат системы
к
называется
матрицей перехода от координат системы
к
 .
.
Теорема
(правило преобразования координат):
! –координатные
строки вектора
в
базах
и
–координатные
строки вектора
в
базах
и
 соответственно. Тогда
соответственно. Тогда
 .
.
Доказательство:
Мы имеем
,
 .
В силу равенства 3 получим, что
.
В силу равенства 3 получим, что
 .
Приравняем координаты, получим, что
.
Приравняем координаты, получим, что
 .
Это равенства равносильны доказательству.
.
Это равенства равносильны доказательству.
Лемма:
! квадратные
матрицы порядка
с
элементами из поля
.
Если
квадратные
матрицы порядка
с
элементами из поля
.
Если
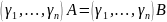 для
строк
с коэффициентами из
,
то
для
строк
с коэффициентами из
,
то
 .
.
Доказательство:
!
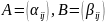 .
Полагаем, что
.
Полагаем, что
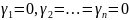 ,
получим
,
получим
 ,
т.е. матрицы
имеют
одинаковые первые строки. Аналогично
полагая,что
,
т.е. матрицы
имеют
одинаковые первые строки. Аналогично
полагая,что
 получим,
что
получим,
что
 и
и
 имеют
одинаковые вторые строки и т.д.
имеют
одинаковые вторые строки и т.д.
Теорема:
Матрица перехода
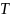 от
координатной системы
к
координатной системе
невырожденная, т.е. имеет образную
матрицу
от
координатной системы
к
координатной системе
невырожденная, т.е. имеет образную
матрицу
 .
При этом
есть
матрица перехода от
к
.
.
При этом
есть
матрица перехода от
к
.
Доказательство:
Правило преобразования координат даёт
нам
.
!
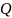 – матрица перехода от координатной
системы
к координатной системе
.
Снова по правилу преобразования
координат мы имеем, что
– матрица перехода от координатной
системы
к координатной системе
.
Снова по правилу преобразования
координат мы имеем, что
 ,
где
координаты
произвольного вектора
.
,
где
координаты
произвольного вектора
.
 – координаты
в
.
Поэтому
– координаты
в
.
Поэтому
 .
В силу леммы
.
В силу леммы
 – единичная матрица
– единичная матрица
 ,
т.е.
,
т.е.
 ,
значит
,
значит
 .
.
Подпространства.
Опр.:
Непустое подмножество
из
называется
подпространством пространства
,
если 1)
 ;
2)
;
2)
 .
т.к.
.
т.к.
 ,
то
,
то
 и
и
 – подгруппа
,
т.е.
– подгруппа
,
т.е.
 .
Если
.
Если
 .
Аналогично проверяются все другие
аксиомы линейного пространства. т.о.
–является
линейным пространством над полем
.
.
Аналогично проверяются все другие
аксиомы линейного пространства. т.о.
–является
линейным пространством над полем
. – тривиальные подпространства
пространства
.
– тривиальные подпространства
пространства
.
Опр.:
!
– произвольные векторы пространства
.
Рассмотрим множество
 .
Очевидно,
– подпространство пространства
.
Это называется линейной оболочкой
векторов
.
Заметим, что если
линейно независимые, то
.
Очевидно,
– подпространство пространства
.
Это называется линейной оболочкой
векторов
.
Заметим, что если
линейно независимые, то
 –база
.
В общем случае
– система образующих пространства
и
–база
.
В общем случае
– система образующих пространства
и
 равно
максимальному числу линейно независимых
векторов этой системы.
равно
максимальному числу линейно независимых
векторов этой системы.
