Ранг матрицы.

Опр.: ! , где –поле. Рассмотрим . Выберем в произвольные строк и столбцов. Составляем определитель из элементов матрицы , стоящих на пересечении этих строк и столбцов. Этот определитель называется минором порядка .

Опр.: Рангом (минорным) матрицы называется число , которое определяется так: , если –нулевая матрица, , если минор порядка матрицы , отличный от нуля, а все миноры порядка равны нулю или .

Опр.: Рангом по строкам (столбцам) называется максимальное число линейно независимых строк (столбцов). Другими словами , где – линейная оболочка строк (столбцов) матрицы .

Опр.: Элементарными преобразованиями строк (столбцов) матрицы называются следующие преобразования: 1) Перестановка 2-х строк (столбцов); 2) Прибавление к одной из строк (одному из столбцов) другой строки (другого столбца), умноженной (умноженного) на некоторый элемент .

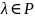Лемма 1: Если получается из элементарным преобразованием, то ранги и по строкам (столбцам) совпадают.

Доказательство: Установим, например, неизменность ранга по строкам при элементарном преобразовании строк. 1) ! получается из элементарным преобразованием 1-го типа. т.к. множество строк матриц и одинаково, то подпространство, порождённое строками матриц и совпадают; 2) Пусть получается из прибавлением к -й строке -й строки, умноженной на . ! – строка матрицы . Тогда – это строка матрицы . Обозначим – линейная оболочка строк матрицы , –так же, то . С другой стороны , поэтому строки содержатся в –т.о. .

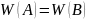Лемма 2: Если получается из элементарным преобразованием, то .

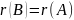Доказательство: Лемма 2 вытекает из свойств определителей.

Теорема (о ранге матрицы): У матрицы все 3 ранга совпадают.

Доказательство: Если – нулевой матрице, то тогда теорема верна в силу определений. ! . Элементарными преобразованиями 1-го типа приводим к виду, где в левом верхнем углу стоит элемент . Элементарными преобразованиями 2-го типа приводим полученную матрицу к виду . Если все элементы кроме равны нулю, то процесс закончился. Если ещё один ненулевой элемент, то элементарными преобразованиями строк и столбцов, с номерами, большими единицы, приводим к виду: , где .Продолжая процесс, мы элементарными преобразованиями приводим к виду , где . Но по виду этой матрицы заключаем, что у не все три ранга равны. В силу лемм 1 и 2 это верно и для матрицы .

Следствие 1: ! – квадратная матрица порядка . 1) строки (столбцы) матрицы линейно независимы, т.е. образуют базу пространства (базу пространства строк или столбцов); 2) строки (столбцы) линейно зависимы (одна из строк (столбцов) есть линейная комбинация остальных).

Следствие 2: матрицы .

Теорема (о ранге произведения матриц): ! – квадратные матрицы порядка . Тогда .

Доказательство: ! 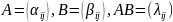. . Тогда , где – -я строка матрицы . т.о. строка матрицы является линейной комбинацией строк матрицы . Поэтому, если – линейная оболочка строк , –линейная оболочка строк (всевозможная линейная комбинация строк – ), то . Далее, .

Следствие: ! – квадратные матрицы порядка , . Тогда .

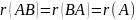Доказательство: ! . По теореме о ранге произведения матриц . В силу условия матрица . Снова по теореме о ранге произведения матриц . Итак, .