
- •Линейная алгебра. Линейное пространство.
- •Линейная зависимость. База. Размерность.
- •Изоморфизм.
- •Координаты.
- •Подпространства.
- •Ранг матрицы.
- •Общая теория линейных систем.
- •Однородное линейное уравнение.
- •Линейные преобразования.
- •Ранг и дефект линейного преобразования.
- •Действия с линейными преобразованиями.
- •Собственные векторы.
- •Инвариантные подпространства.
- •Многочленные матрицы.
- •Элементарные делители.
- •Нормальная форма Жордана.
- •Унитарные и Евклидовы пространства.
- •Ортогональные суммы.
- •Ортогональное дополнение.
Линейная алгебра. Линейное пространство.
Опр.:
Множество
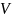 называется
линейным (векторным) пространством над
полем
называется
линейным (векторным) пространством над
полем
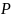 ,
если: 1) На
определена
бинарная алгебраическая операция
,
если: 1) На
определена
бинарная алгебраическая операция
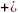 и
и
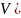 –Абелева
группа,
–Абелева
группа,
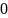 – нулевой элемент
;
2)
– нулевой элемент
;
2)
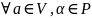 однозначно
определен элемент
однозначно
определен элемент
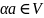 и
при этом выполняются следующие аксиомы:
и
при этом выполняются следующие аксиомы:
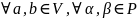 :
:
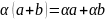 ,
,
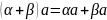 ,
,
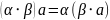 ,
,
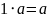 .
.
Линейная зависимость. База. Размерность.
Пусть – линейное пространство над полем .
Опр.:
Пусть
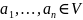 ,
,
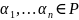 .
Вектор
.
Вектор
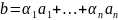 называется
линейной комбинацией векторов
называется
линейной комбинацией векторов
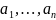 .
.
Опр.:
Конечная система векторов
называется
линейно независимой, если
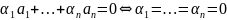 .
.
Опр.:
Бесконечная система векторов
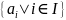 называется
линейно независимой, если
называется
линейно независимой, если
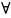 её
конечная подсистема линейно независимая.
её
конечная подсистема линейно независимая.
Опр.: Система векторов называется системой образующих пространства , если вектор из является линейной комбинацией этой системы.
Опр.: Бесконечная система векторов называется системой образующих пространства , если вектор из есть линейная комбинация конечной подсистемы этих векторов.
Опр.: Базой пространства называется линейно независимая система образующих пространства .
Опр.:
Линейное пространство
называется
конечномерным, если в нём
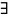 база
из конечного числа векторов.
база
из конечного числа векторов.
Лемма
1: Система векторов
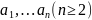 линейно
зависима
линейно
зависима
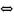 хотя
бы один из этих векторов есть линейная
комбинация остальных.
хотя
бы один из этих векторов есть линейная
комбинация остальных.
Доказательство:
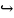 !
– линейно зависимые
!
– линейно зависимые
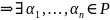 ,
хотя бы один из которых отличен от 0 и
,
хотя бы один из которых отличен от 0 и
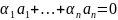 .
!, например,
.
!, например,
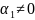 ,
т.е.
,
т.е.
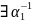 .
Тогда умножаем на
.
Тогда умножаем на
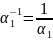 .
Получаем
.
Получаем
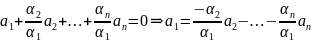 ,
т.е.
,
т.е.
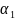 – линейная комбинация остальных
векторов.
– линейная комбинация остальных
векторов.
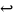 !, например,
!, например,
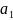 – есть линейная комбинация остальных
векторов. Тогда
– есть линейная комбинация остальных
векторов. Тогда
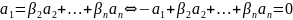 ,
т.к. коэффициент при
отличен
от 0, то
–линейно
зависимые по определению.
,
т.к. коэффициент при
отличен
от 0, то
–линейно
зависимые по определению.
Лемма 2: Система ненулевых векторов линейно зависима хотя бы один из векторов системы есть линейная комбинация предыдущих.
Доказательство:
!
система векторов
–это
линейно зависимые векторы
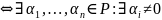 и
и
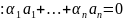 .
Понятно, что
максимальное
число
.
Понятно, что
максимальное
число
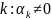 .
Очевидно, что
.
Очевидно, что
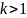 и
и
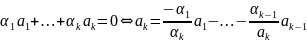 ,
т.е.
,
т.е.
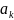 – линейная комбинация предыдущих
векторов.
!
– линейная комбинация предыдущих
векторов.
!
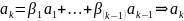 – линейная комбинация остальных
векторов системы:
– линейная комбинация остальных
векторов системы:
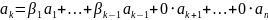 .
По лемме 1 получается, что система
линейно независимая.
.
По лемме 1 получается, что система
линейно независимая.
Лемма
3: !
– система образующих пространства
.
Если
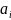 – линейная комбинация остальных
векторов системы, то, выбросив
– линейная комбинация остальных
векторов системы, то, выбросив
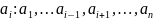 –тоже
система образующих
.
–тоже
система образующих
.
Доказательство:
!
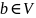 .
По условию,
.
По условию,
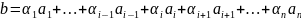 .
Согласно условию
.
Согласно условию
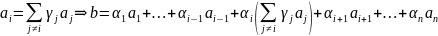 .
Раскрывая скобки и приводя подобные,
мы установим, что
.
Раскрывая скобки и приводя подобные,
мы установим, что
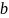 – линейная комбинация всех векторов
системы кроме
.
– линейная комбинация всех векторов
системы кроме
.
Теорема
1: !
– база пространства
,
тогда
система
из
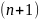 вектора
линейно зависима.
вектора
линейно зависима.
Доказательство:
! напротив найдётся линейно независимая
система
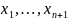 .
Рассмотрим систему
.
Рассмотрим систему
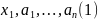 .
Она линейно зависима по лемме 1 и условию
теоремы. Согласно лемме 2, один из
векторов системы (вектор
)
есть линейная комбинация предыдущих.
Ясно, что
.
Она линейно зависима по лемме 1 и условию
теоремы. Согласно лемме 2, один из
векторов системы (вектор
)
есть линейная комбинация предыдущих.
Ясно, что
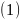 остается системой образующих, а, значит,
по лемме 3
остается системой образующих, а, значит,
по лемме 3
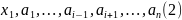 –
система образующих пространства
.
Рассмотрим теперь систему
–
система образующих пространства
.
Рассмотрим теперь систему
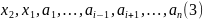 ,
которая является линейно зависимой по
лемме 1. Согласно лемме 2, один из этих
векторов
,
которая является линейно зависимой по
лемме 1. Согласно лемме 2, один из этих
векторов
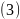 есть линейная комбинация предыдущих.
т.к.
есть линейная комбинация предыдущих.
т.к.
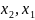 – линейно независимые, то это некоторый
вектор
– линейно независимые, то это некоторый
вектор
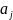 .
Тогда согласно леммы 3:
.
Тогда согласно леммы 3:
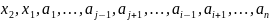 –система
образующих пространства
.
Рассуждая аналогичным образом, получим,
что
–система
образующих пространства
.
Рассуждая аналогичным образом, получим,
что
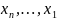 – система образующих пространства
.
Но тогда
– система образующих пространства
.
Но тогда
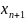 – линейная комбинация этих векторов,
что невозможно в силу леммы 1. А это уже
противоречие с леммой 1.
– линейная комбинация этих векторов,
что невозможно в силу леммы 1. А это уже
противоречие с леммой 1.
Теорема
2: Если
–база
,
то
база
пространства
состоит
из
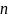 векторов.
векторов.
Доказательство: Теорема 2 является непосредственным следствием теоремы 1.
Опр.:
Число элементов базы линейного
пространства
называется
размерностью пространства
и
обозначается
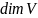 .
.
Теорема
3 (о дополняемости линейно независимой
системы векторов до базы): !
– линейно независимые вектора
пространства
,
тогда найдутся такие векторы
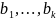 пространства
,
что
пространства
,
что
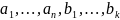 –база
.
–база
.
Доказательство:
!
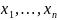 – база
.
Рассмотрим следующую систему
– база
.
Рассмотрим следующую систему
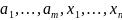 ,
которая является системой образующих
пространства. Выбросим из этой системы
все векторы, которые являются линейными
комбинациями предыдущих. т.к.
,
которая является системой образующих
пространства. Выбросим из этой системы
все векторы, которые являются линейными
комбинациями предыдущих. т.к.
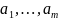 линейно
независимы, то мы получим систему
векторов
линейно
независимы, то мы получим систему
векторов
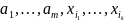 .
Эта система линейно независима по лемме
2 и система образующих по лемме 3. Итак,
.
Эта система линейно независима по лемме
2 и система образующих по лемме 3. Итак,
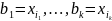 – искомые векторы.
– искомые векторы.
