Решение:

1) АВ ={-12; -5}, |AB|=13

BC = {-4; 3}, |BC|=5

AC = {-16; -2}, |AC|= =

2) AM=0.5(AB +AC)=0.5{-12-16; -5-2}= {-28;-7}

|AM| = √(-28)² +(-7)² = 7√17

3)Имеем уравнение прямой ВС:

x +5	=	y -4
-4		3

3x + 4y – 1 = 0.

|AH| = ρ(A, BC) =	|3∙7+4∙1–1|	=4,8

4) Найдем уравнение прямой AL:

;

Значит,

.

Тогда, 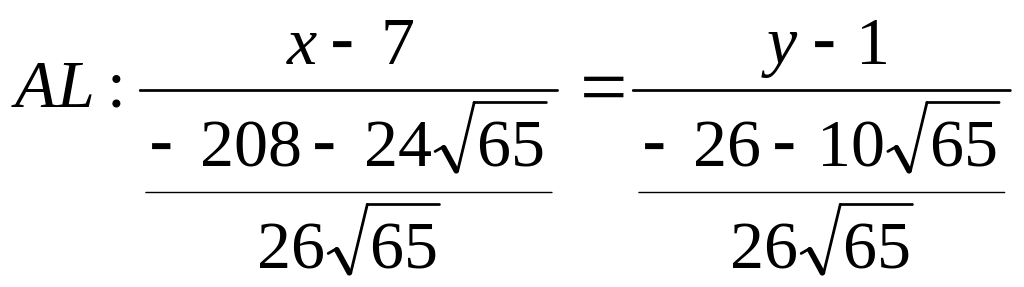или

5)

Задача 3. С помощью преобразования поворота прямоугольной декартовой системы привести к каноническому виду уравнение кривой второго порядка

9x² - 24 xy + 16y² + 30x - 40y – 25 = 0.

Написать формулы преобразования и изобразить данную кривую на чертеже.

РЕШЕНИЕ:

.

Получили:

, где .

Канонический вид уравнения заданной кривой:

Это гипербола с вершинами в точках и ; асимптотами и фокусами и

Задача 4. Найти точки пересечения кривой второго порядка γ с прямой (а):

γ: x² – 2xy – 3y² – 4x – 6y +3 = 0,

a: x=t

y=5t-5.

РЕШЕНИЕ:

так как x=t , то получим 5x – y – 5 = 0

Решим систему уравнений:

x ² – 2xy – 3y² – 4x – 6y +3 = 0,

5x – y – 5 = 0.

y = 5(x-1),

x² –10x(x–1) – 3∙25(x–1)² – 4x – 30(x–1) + 3 = 0.

y = 5(x-1),

-84x² +126x – 42 = 0.

Решим второе уравнение системы:

42x² – 63x + 21 = 0

D=3969-3528=21²

x1 =	63+21	=1,
	42∙2

x2 =	63–21	=	1
	42∙2		2

Имеем:

x = 1, y = 5(x–1) = 0.

и

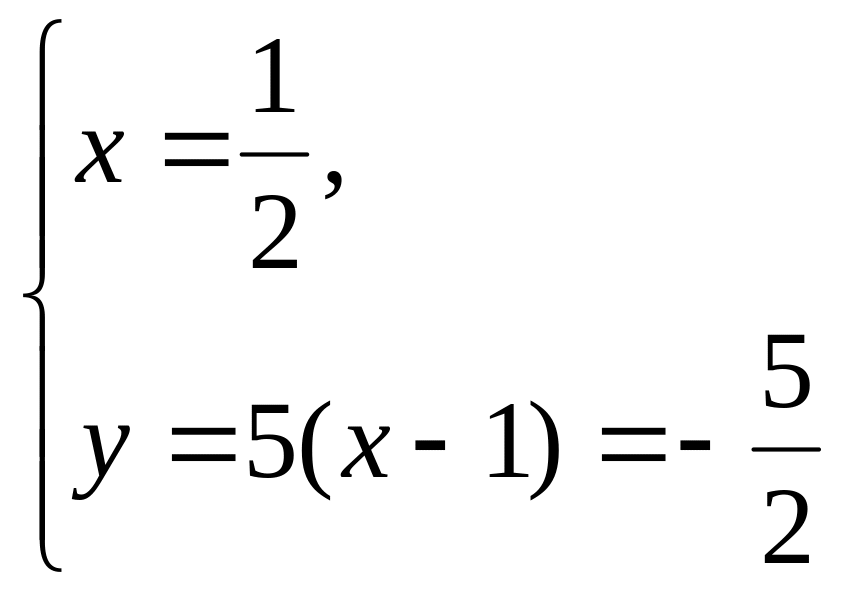
Ответ: (1;0) и

Задача 5. Для одинаково ориентированных реперов R(O, i, j) и R’(O’, i’, j’) на плоскости написать формулы преобразования R в R’, если точка O’ имеет координаты (x₀, y₀) относительно R, а угол между векторами i и i’ равен α.

Найти координаты точек M(x₁, y₁), N(x₂,y₂) и уравнение прямой (а) 2x–4y+5=0 в репере R’, если точки M,N и прямая (a) заданы в репере R.

O’(-3; 2), α=5π/4, M(0,10), N(1, ).

РЕШЕНИЕ:

1) Имеем:

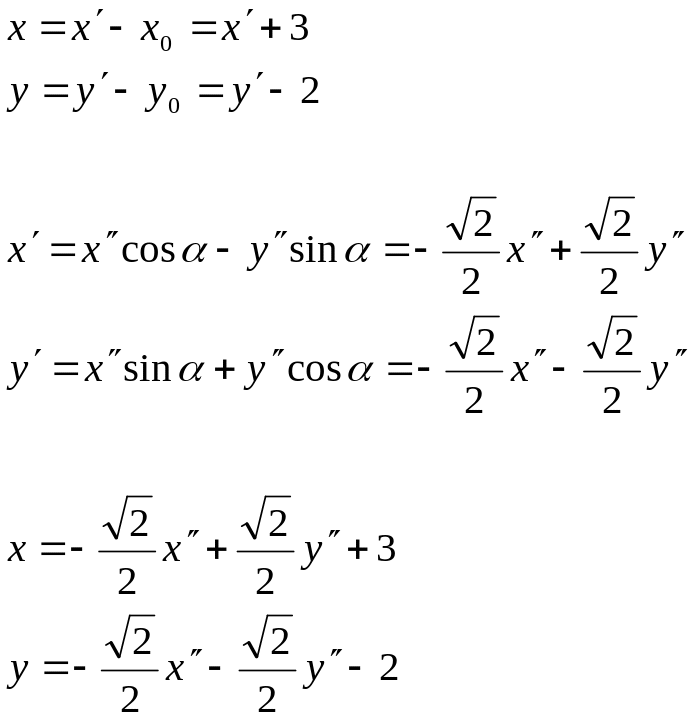
2) Найдем уравнение прямой :

3) Найдем координаты точки :

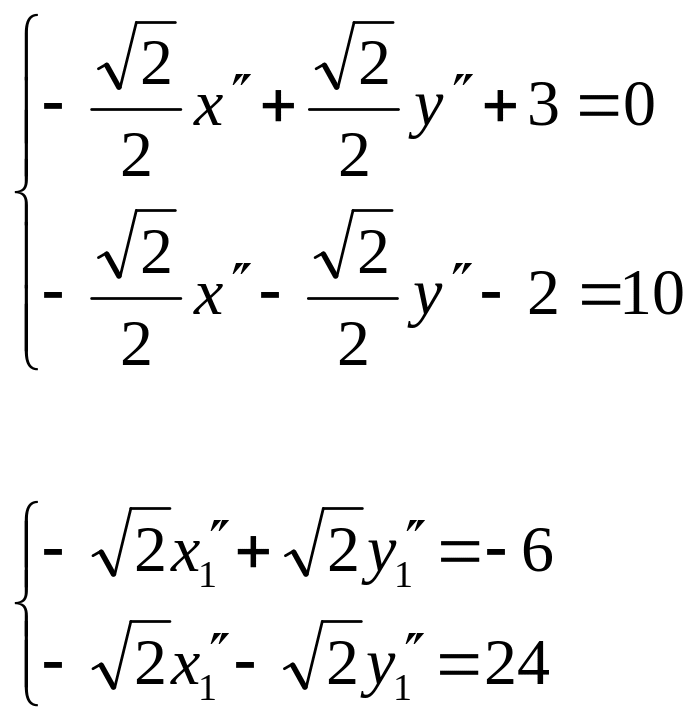
Итак,

4) Найдем координаты точки :

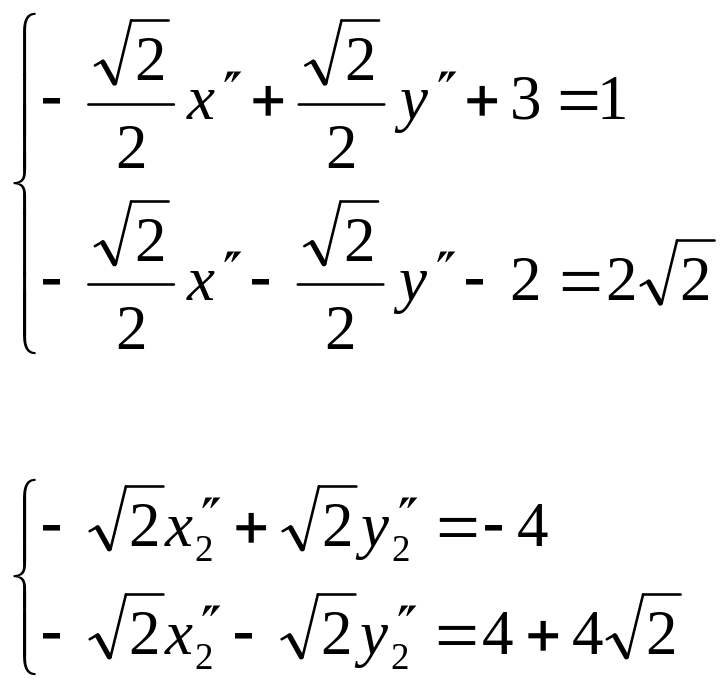
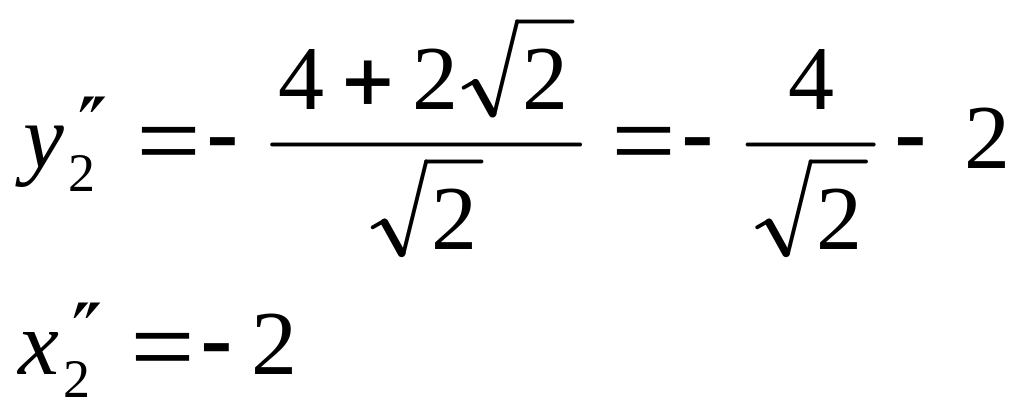
Итак,

Ответ: , ,

Задача 6. Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось направлена по биссектрисе первого координатного угла. Даны полярные координаты точек M(ρ₁, φ₁), N(ρ₂, φ₂). Определить декартовы координаты этих точек.

M(1, 2π/3), N(3, 4π/3)

РЕШЕНИЕ:

M(x_M; y_M), где

x_M=ρ₁Cos (φ₁+4π/3) = Cos(2π)=1

y_M=ρ₁Sin (φ₁+4π/3) = Sin(2π) =0

N(x_N; y_N), где

x_N=ρ₂Cos (φ₂+4π/3) = 3Cos(8π/3)

y_N=ρ₂Sin (φ₂+4π/3) = 3Sin(8π/3)

Ответ: M(1;0); N(3Cos(8π/3); 3Sin(8π/3))

Задача 7. Для векторов а(4; 3; -1), b(5; 0;4), c(2; 1; 2), заданных в ортонормированном базисе R(O, i, j, k), найдите:

1. направляющие косинусы вектора а;

2. площадь параллелограмма, построенного на векторах а и с, имеющих общее начало;

3. объем пирамиды, построенной на векторах а, b и с, имеющих общее начало;

РЕШЕНИЕ:

1)	Cos α =	ax	=	4	=	4
		|a|

	Cos β =	ay	=	3
		|a|

	Cos γ =	az	=	-1
		|a|

2) S = |[a, c]|.

[a, c] =	i	j	k	= 7i +6j - 2k
	4	3	-1
	2	1	2

S = =

3) V = |a∙b∙c|.

a∙b∙c =	4	3	-1	= -25
	5	0	4
	2	1	2

V = 25

Ответ: ; 25

Задача 8. Найти расстояние между двумя прямыми

x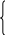 = 2t – 4, x = 4t – 5,

y = –t + 4, и y = –3t + 5,

z = –2t – 1 z = –5t + 5.

РЕШЕНИЕ:

Здесь M₁(-4, 4, -1); M₂(-5, 5, 5); ={2, -1, -2}; ={4, -3, -5}

=	2	-1	-2	=	0	-1	0	= -9
	4	-3	-5		-1	-3	1
	-1	1	6		5	1	4

[ , ] =	i	j	k	= -i – 2j – 2k
	2	-1	-2
	4	-3	-5

Ответ: 3

Задача 9. Найти каноническое уравнение прямой, проходящей через точку А₄ перпендикулярно плоскости, проходящей через точки А₁, А₂, А₃, если А₁(0;0;2), А₂(3;0;5), А₃(1;1;0), А₄(4;1;2).