
Решение:
Рассмотрим:
1) A1(λx)=(7λx1+6λx2–λx3+3λx4, 5λx1–4λx2+λx3–2λx4, 3λx1+2λx2, λx1) = (λ(7x1+6x2–x3+3x4), λ(5x1–4x2+x3–2x4), λ(3x1+2x2), λx1) = λA1(x)
2) A1(x+y)=(7(x1+y1)+6(x2+y2)–(x3+y3)+3(x4+y4), 5(x1+y1)–
–4(x2+y2)+ (x3+y3)–2(x4+y4), 3(x1+y1)+2(x2+y2), (x1+y1)) = (7x1+6x2–
–x3+3x4, 5x1–4x2+x3–2x4, 3x1+2x2, x1)+ (7y1+6y2–y3+3y4, 5y1–4y2+y3–
–2y4, 3y1+2y2, y1)= A1(x)+A1(y)
Итак, A1(λx)=λA1(x) и A1(x+y)= A1(x)+A1(y), значит оператор A1 – линейный.
3) Найдем матрицу оператора в каноническом базисе R3 :
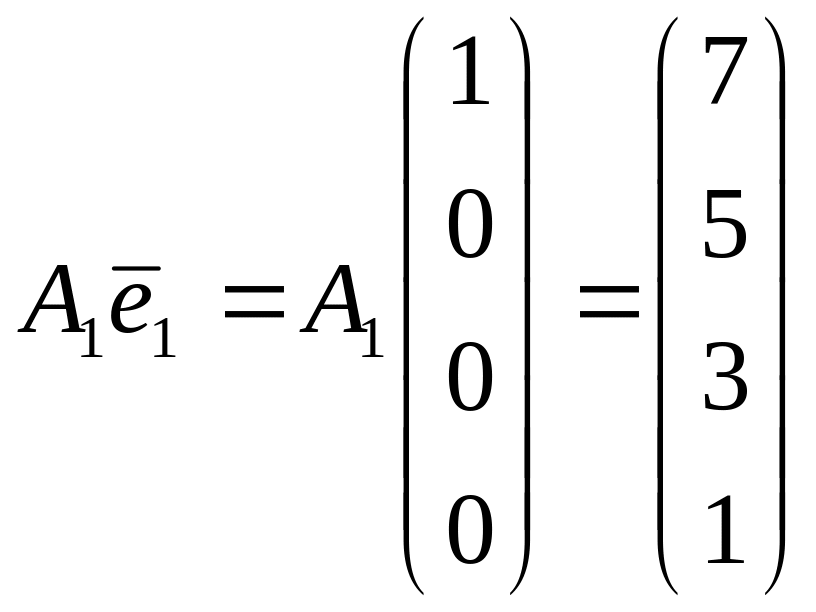 ,
,
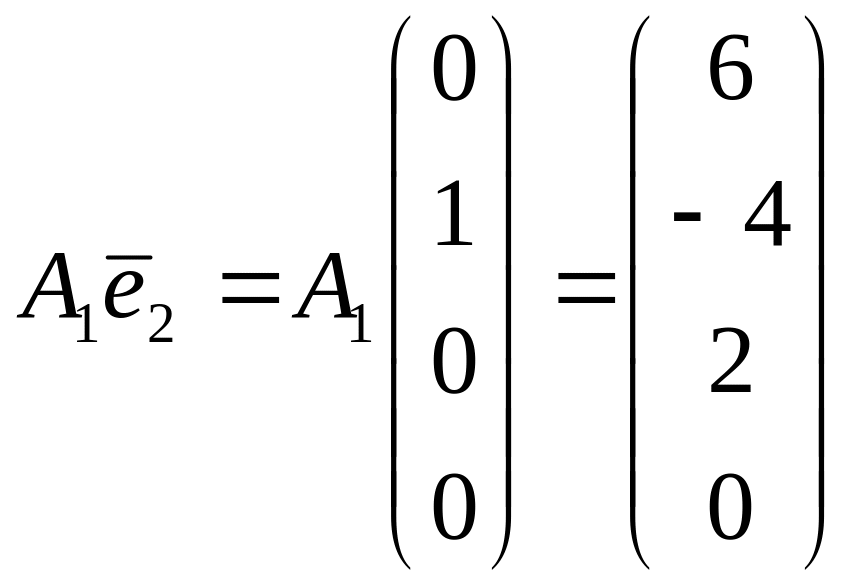 ,
,
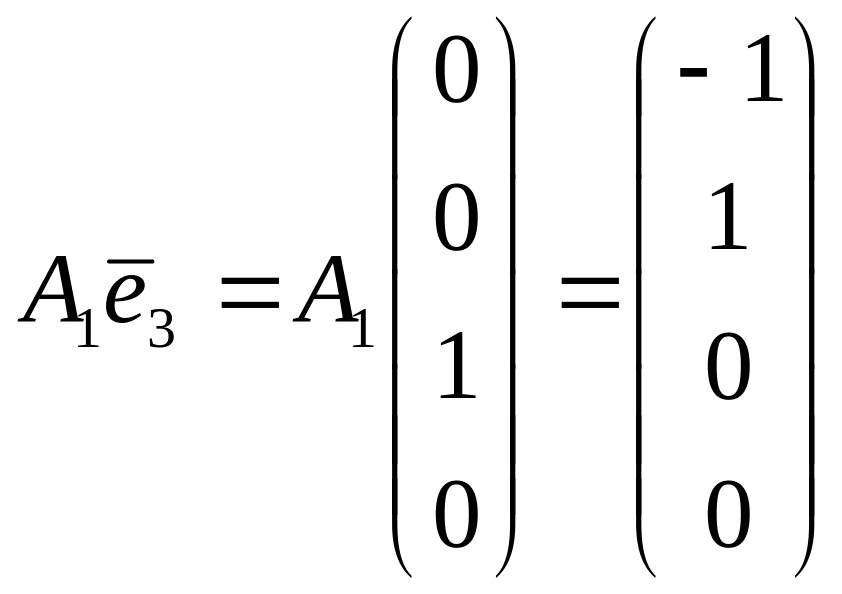 ,
,
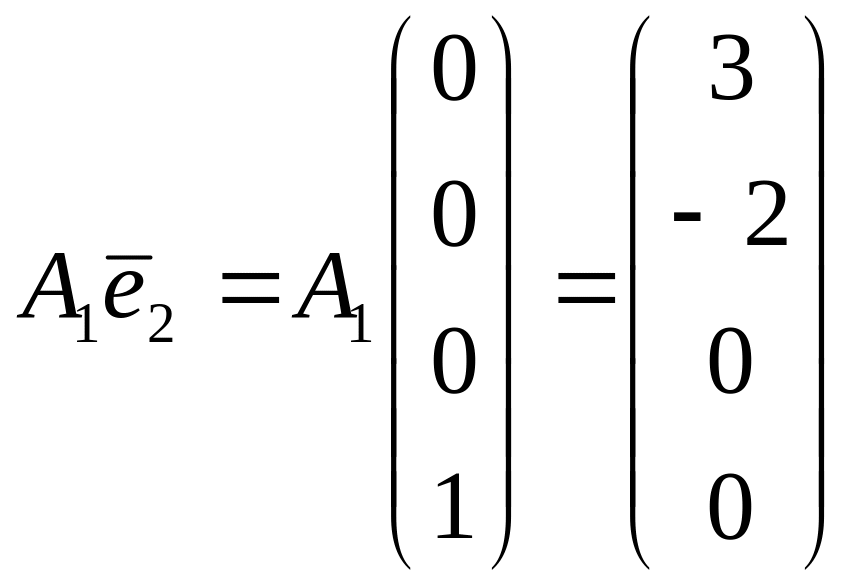 .
.
Значит,
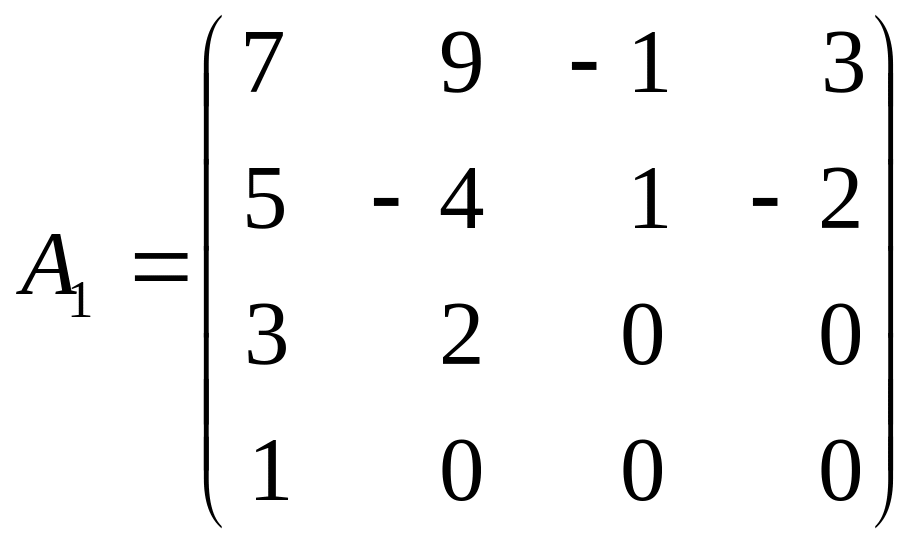 – матрица данного линейного оператора
– матрица данного линейного оператора
4)
Найдем ранг оператора, т.е. размерность
его образа TA.
По определению
![]() тогда и только тогда, когда найдется
вектор
тогда и только тогда, когда найдется
вектор
![]() такой, что
такой, что
![]() или, в координатной записи:
или, в координатной записи:

Это
означает, что образ TA
совпадает с линейной оболочкой системы
столбцов матрицы А1.
Следовательно, ранг оператора А1
совпадает с рангом его матрицы, т.е.
равен 3. Тогда дефект оператора А1:
![]() .
.
2. Рассмотрим
A2(λx)=(5λx1+4λx2–λx3, –2λx2+3λx3, 3λx1+2λx2+2λx3–1)
λA2(x)=(5λx1+4λx2–λx3,
–2λx2+3λx3,
3λx1+2λx2+2λx3–λ)![]() A2(λx)
A2(λx)
Следовательно, A2 не является линейным оператором.
Задача 6. Найти собственные значения и собственные векторы линейного оператора, заданного в некотором базисе матрицей:

РЕШЕНИЕ:
1. Найдем определитель:
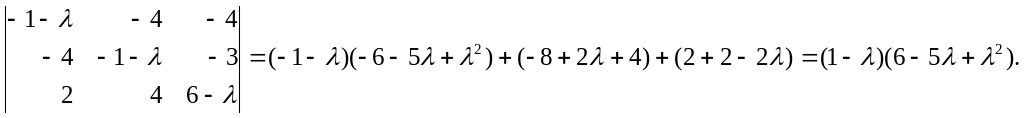
2. Решим уравнение:
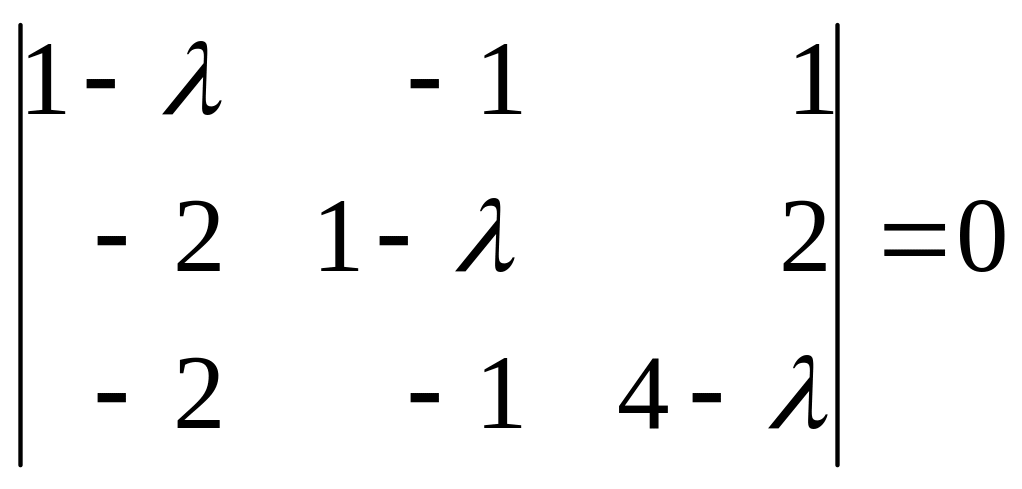
![]()
![]() или
или
![]()
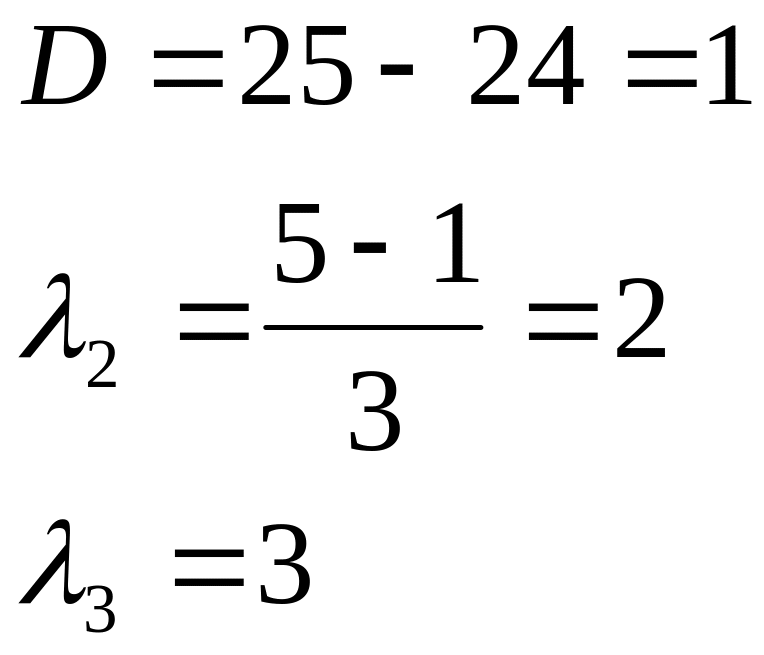
3. Итак,
имеем собственные
значения
линейного оператора:
,
![]()
![]()
4. Найдем собственные векторы, отвечающие:
а) .
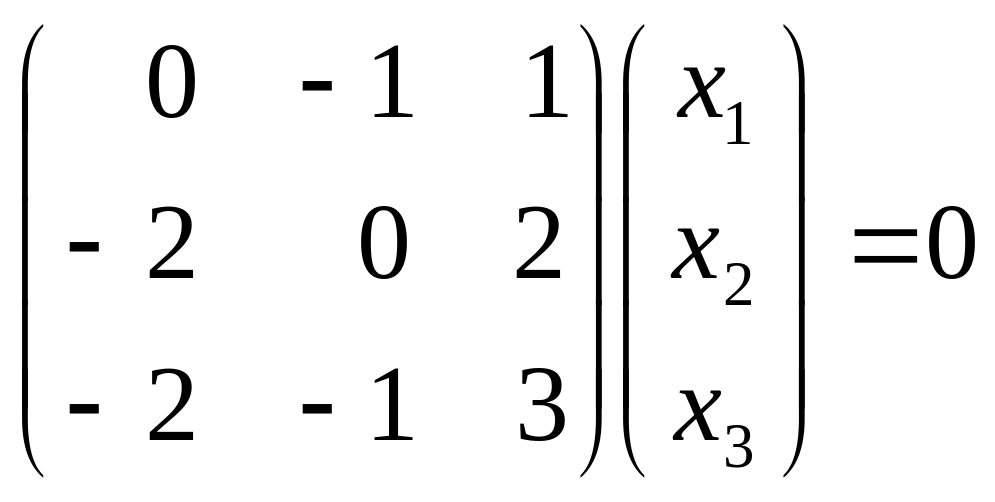
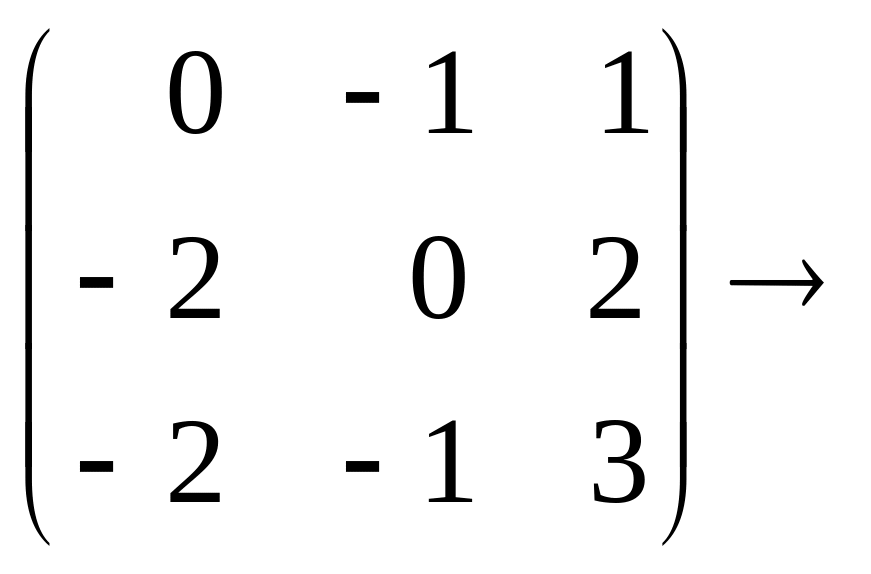
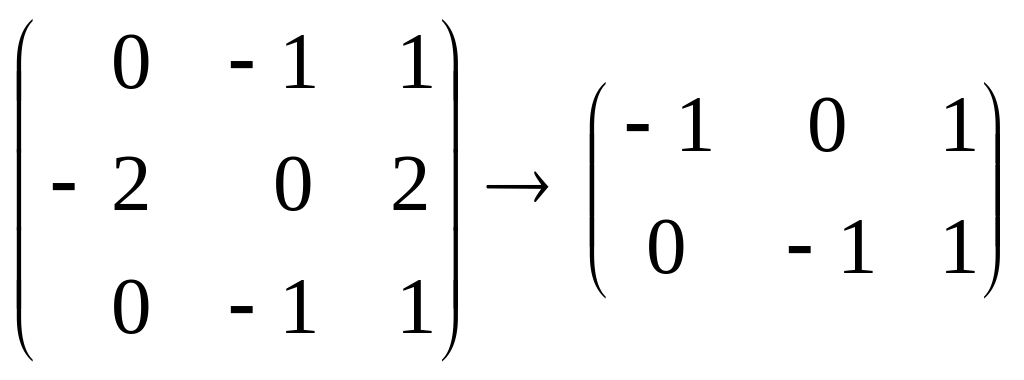
Пусть x1 и x2 – базисные переменные, x3=с – свободная. Тогда
x1=с, x2=с.
Имеем
собственный
вектор линейного оператора,
отвечающий собственному значению
:
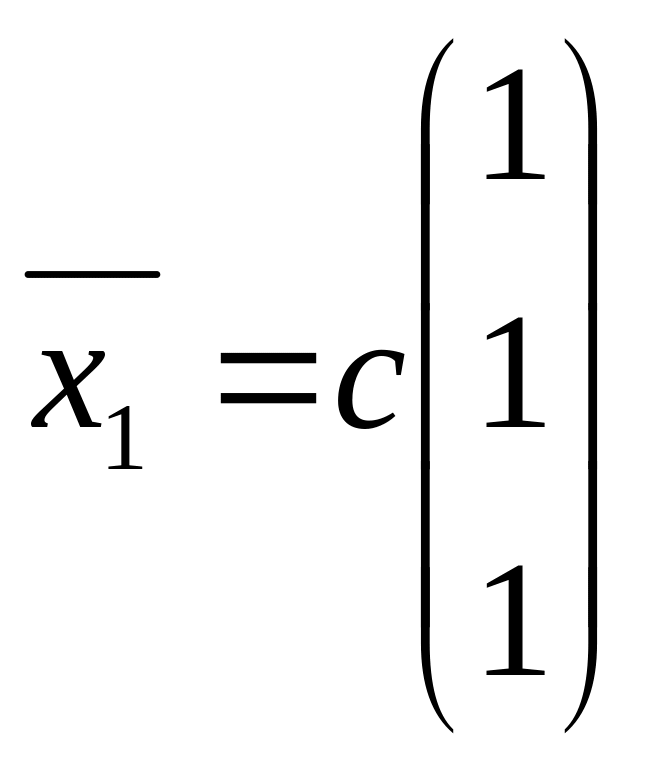 .
.
б)
![]() .
.
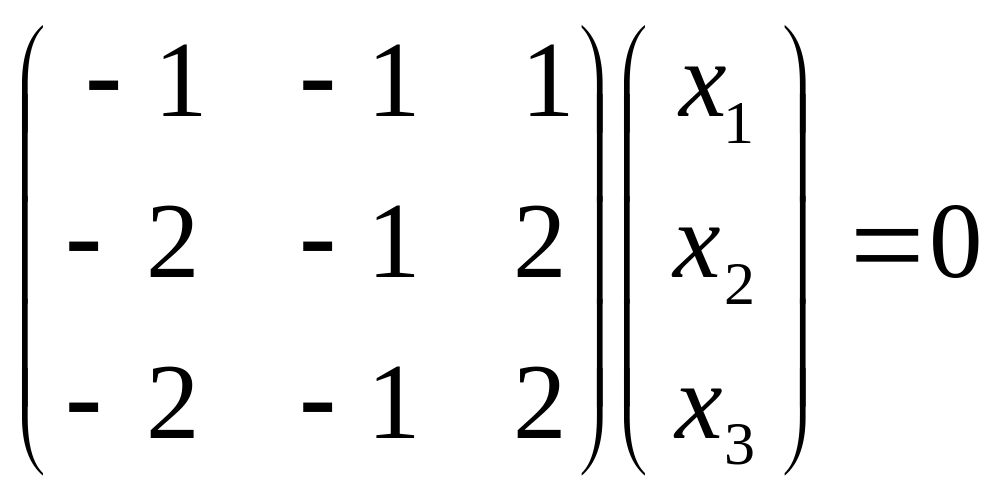
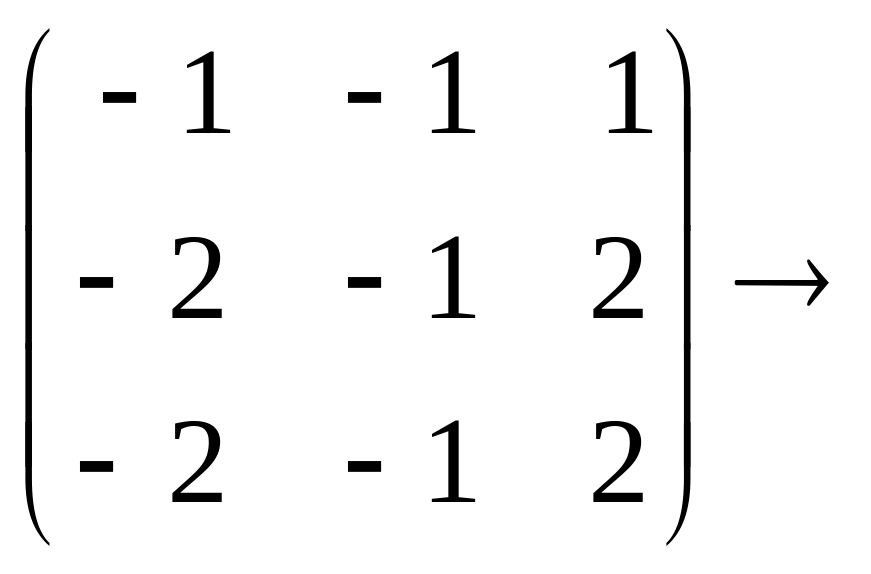
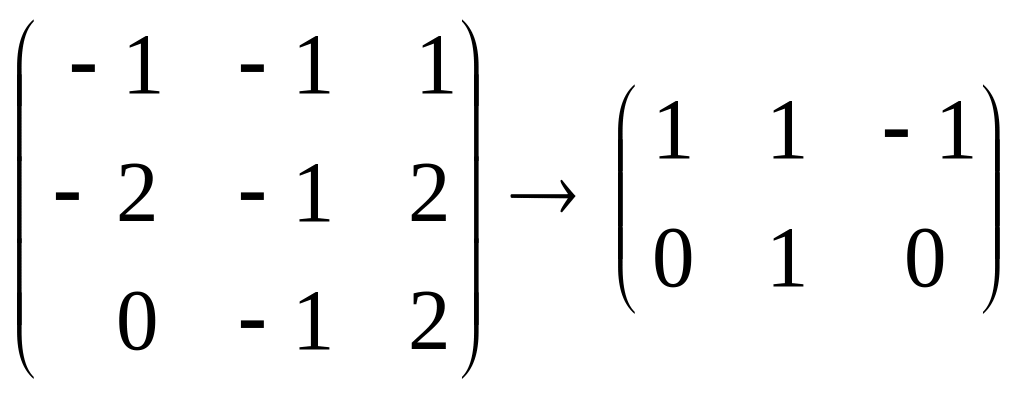
Пусть x1 и x2 – базисные переменные, x3=с – свободная. Тогда
x2=0, x1= – x2+с=с
Имеем
собственный
вектор линейного оператора,
отвечающий собственному значению
:
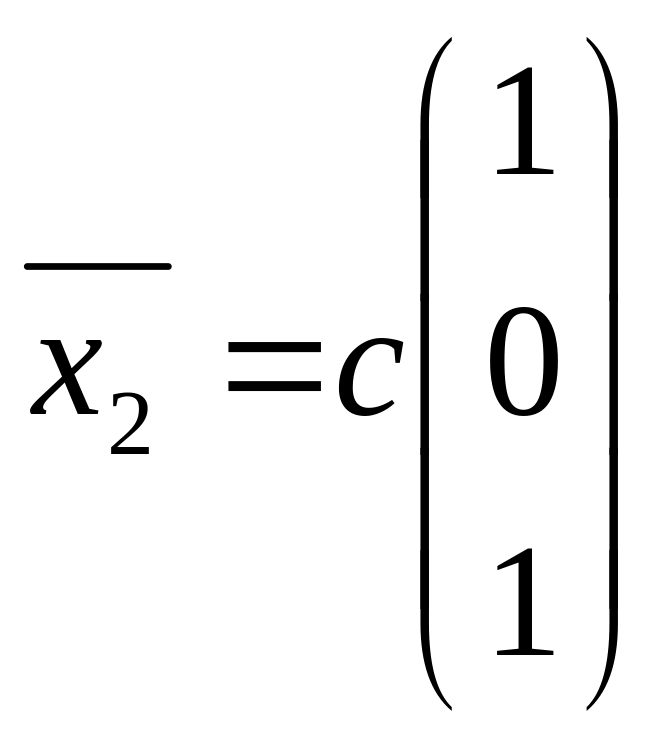 .
.
в)
![]() .
.
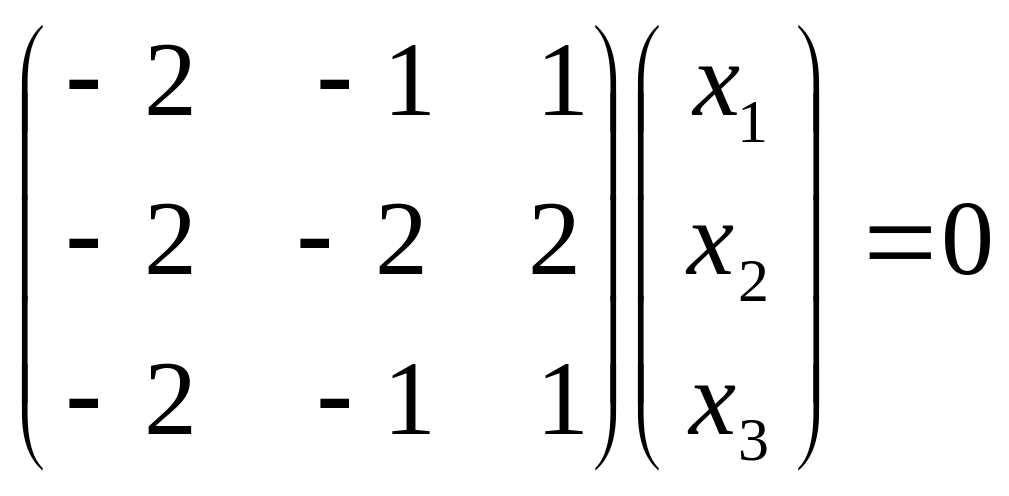
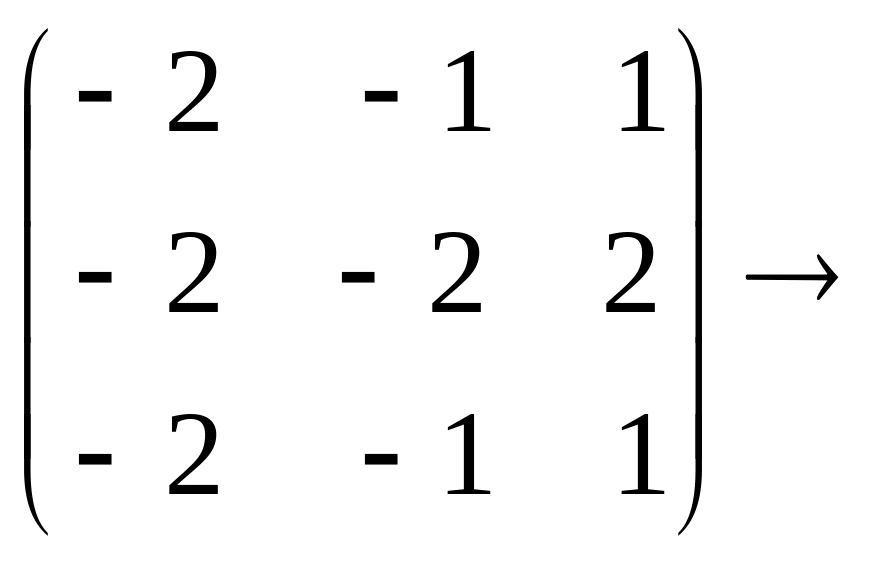
![]()
Пусть x1 и x2 – базисные переменные, x3=с – свободная. Тогда
![]()
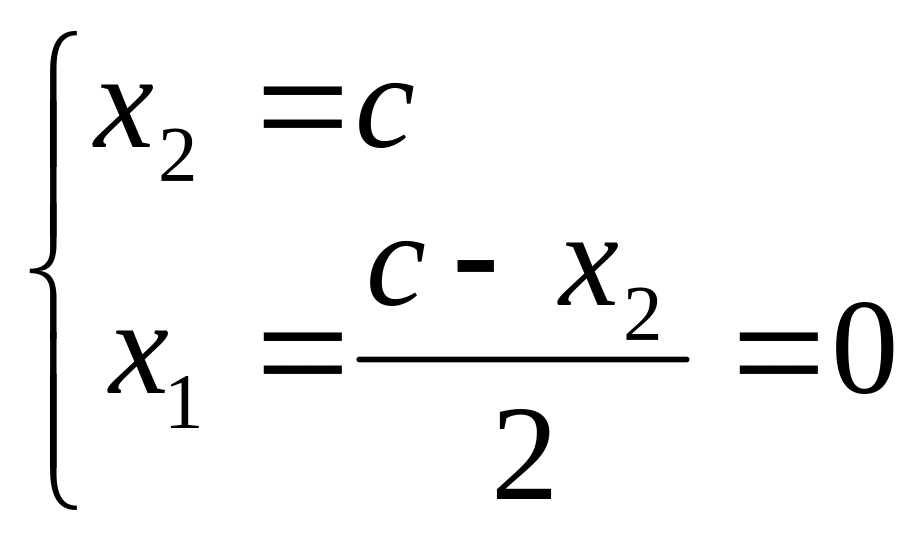
Имеем
собственный
вектор линейного оператора,
отвечающий собственному значению
:
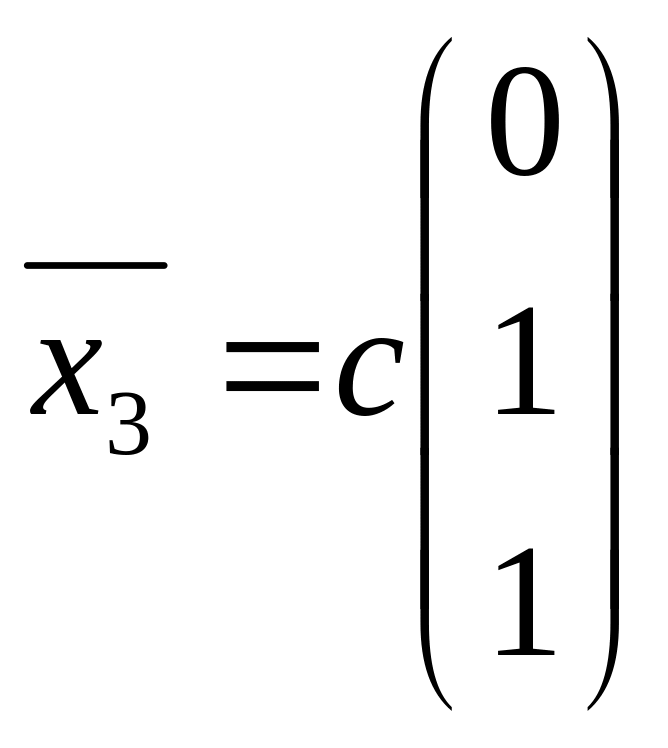 .
.
III. Квадратичные формы, квадрики. Элементы дифференциальной геометрии.
Задача 1. Привести к каноническому виду уравнение квадрики, установить вид квадрики. Написать формулы перехода к новой системе координат, найти координаты новых координатных векторов и нового начала относительно старой системы координат в двумерном аффинном пространстве А2:
x12 + 4x1x2 + 4x22 – 4x1 – 4x2 – 12 = 0.
Решение:
Рассмотрим матрицу квадратичной формы:
![]() .
.
1) Найдем собственные значения:
![]()
![]()
![]() и
и
![]()
Определим, собственные векторы для:
а)
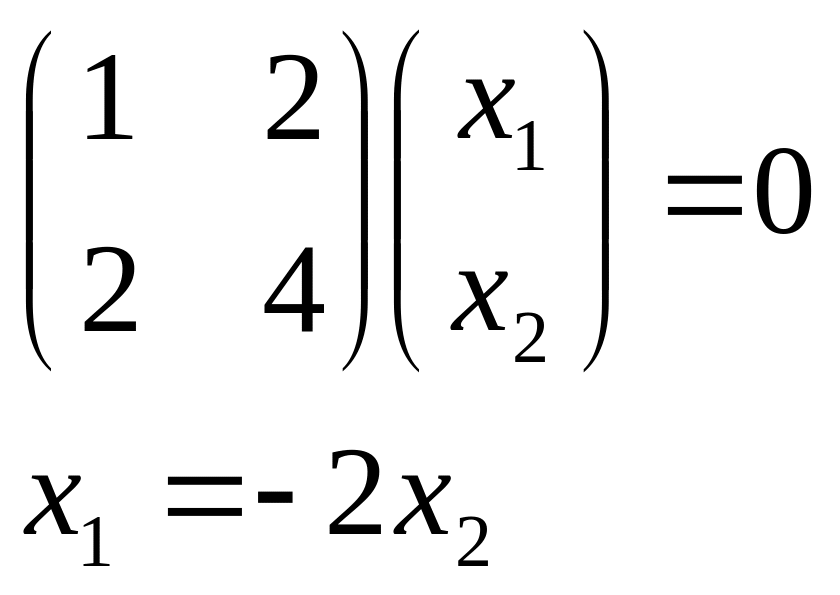
Имеем
собственный нормированный вектор:
![]() .
.
б)
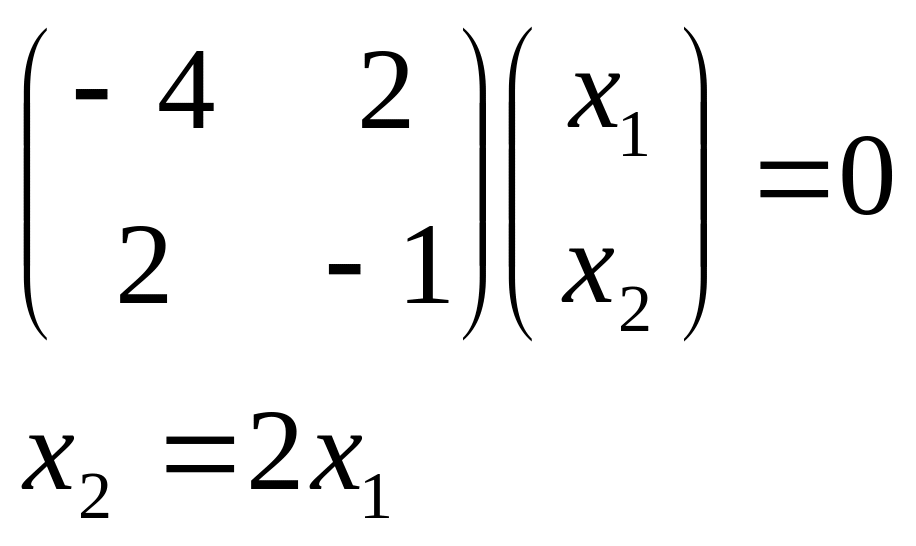
Имеем
собственный нормированный вектор:
![]() .
.
2)
Матрица перехода от ортонормированного
базиса
![]() к
к
![]() имеет вид:
имеет вид:
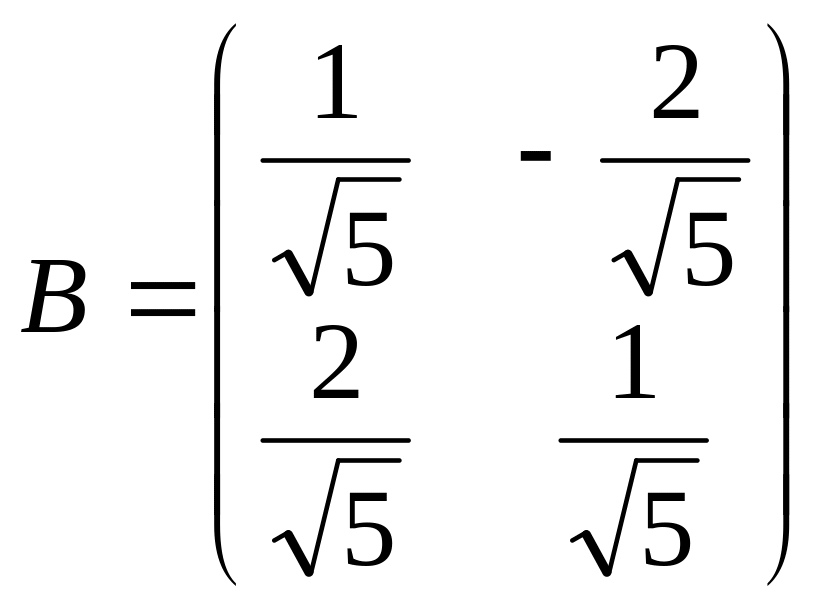
Получаем формулы преобразования координат:
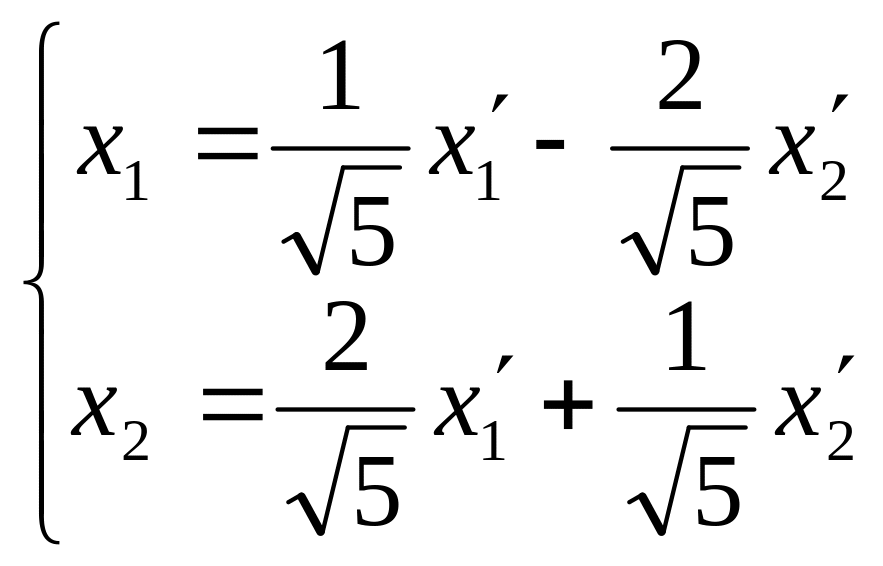 (*)
(*)
Подставляем в форму:
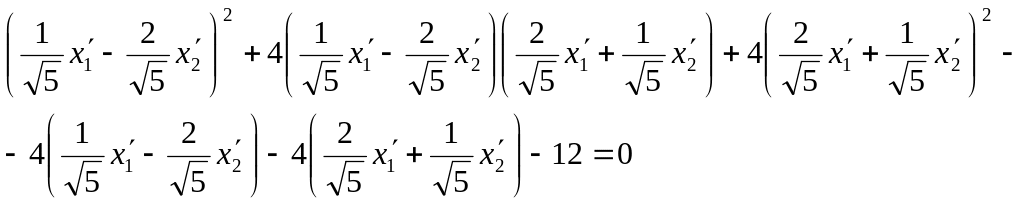
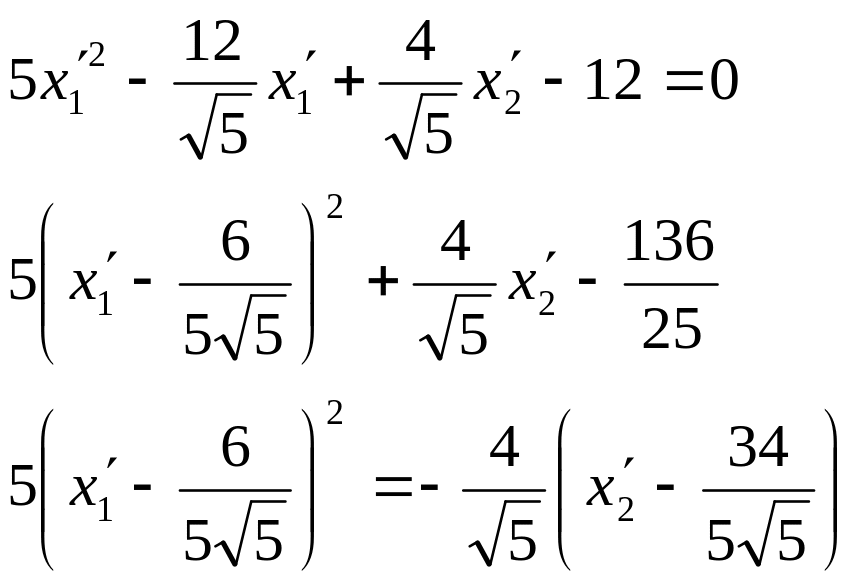
![]()
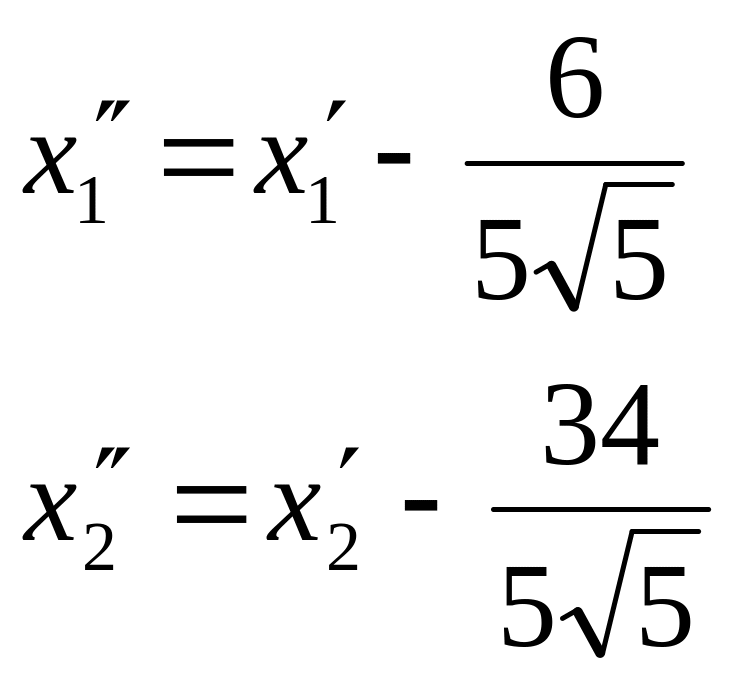
![]()
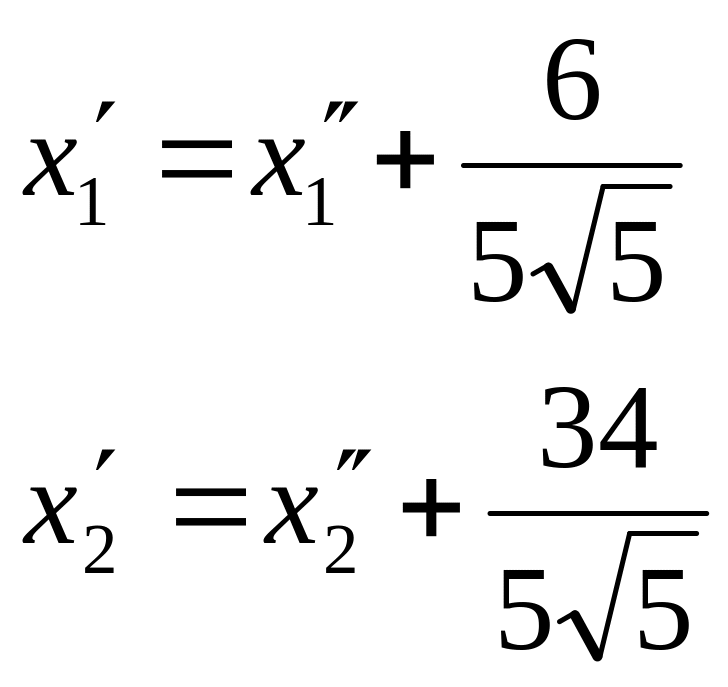
Подставляем в (*):
![]()
![]()
Итак, имеем формулы перехода к новой системе координат:
![]() ;
;
![]()
3)
Имеем:![]()
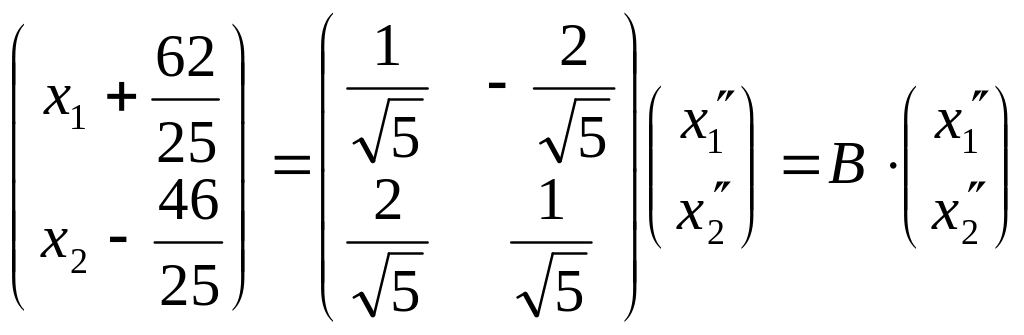
Тогда,
![]() .
.
Т.
к. матрица B
– ортогональная, то
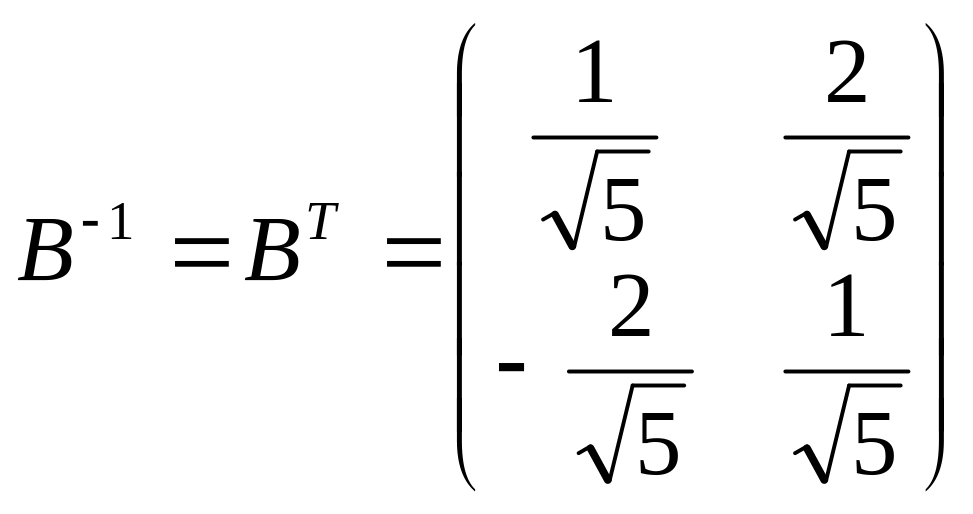 .
.
Поэтому
![]()
![]() .
.
Значит,
новое начало координат находится в
точке
![]() .
.
Ответ: ; ; .
Часть третья Аналитическая геометрия.
|
Задача 1. Найти уравнение диагонали параллелограмма, не проходящей через точку пересечения его сторон x+y–1=0 и y+1=0, если известно, что диагонали параллелограмма пересекаются в точке Р(-1;0).
РЕШЕНИЕ:
1)
Найдем точку А
– точку пересечения сторон x +y–1=0
и y+1=0
+y–1=0
и y+1=0
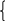 x
+ y
– 1= 0,
x
+ y
– 1= 0,
y + 1 = 0.
y = -1,
x = 2.
Значит, А имеет координаты (2;-1).
Имеем уравнение прямой АС:
-
x – 2
=
y + 1
-3
1
АС: x +3y +1 = 0
2) Найдем координаты точки С:
 |PC|=|AP|=√(x+1)2
+ y2
|PC|=|AP|=√(x+1)2
+ y2
|AP|=√(-1-2)2+(0+1)2 = √10
( x+1)2 + y2 = 10
x +3y +1 = 0
x = -3y –1
(-3y–1+1)2 + y2 = 10
x = -3y –1
y2 = 1
-
y = -1,
x = -3y – 1 = 2.
или
y = 1,
x = -4.
Это координаты точки А
Точка С имеет координаты (-4; 1)
3) ВС||AD, поэтому уравнение прямой ВС: (x+4) +(y-1) = 0
x+y+3=0
4) Найдем координаты точки В, как точки пересечения прямых АВ и ВС:
x + y +3 = 0
y + 1= 0
y = -1
x = -3–y = -2
Точка В имеет координаты (-2;-1).
5) Имеем уравнение прямой BD, проходящей через точки В(-2;-1) и Р(-1;0):
x + 2 |
= |
y + 1 |
1 |
1 |
Ответ: x – y +1 = 0
Задача 2. Даны координаты вершин треугольника АВС. Найти длины медианы, высоты, биссектрисы, проведенных из вершины А. Вычислить внутренний угол при вершине В.
А (7;1), В(-5; –4); С(-9;-1).
