Линейные пространства

Задача 1. Выяснить, являются ли линейно независимыми системы элементов:

1. a₁=4x, a₂=1–x+x², a₃=2+4x, a₄=(3-х)³, a₅=(1-x)⁴, a₆=(1+x)⁵.

2) , , ,

3) a=(2, -3, 1, 5), b=(1, 3, 2, -4), c=(-1, 9, 2, 0)

Решение:

1)

Следовательно, эта система элементов линейно зависима.

2) Очевидно, что .

Действительно,

Следовательно, эта система элементов линейно зависима.

3) Рассмотрим линейную комбинацию λ₁a+λ₂b+λ₃c. Предположим, что система линейно зависима, тогда должна иметь нетривиальное решение следующая систему уравнений:

Найдем ранг матрицы системы:

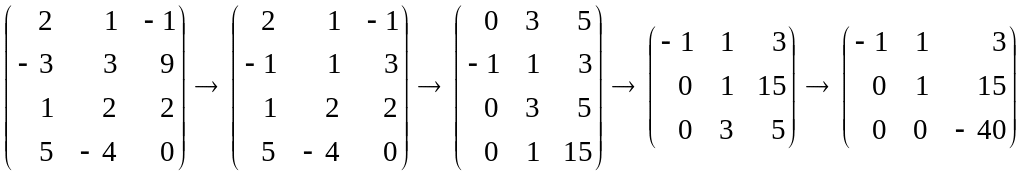
Ранг матрицы системы равен количеству неизвестных, следовательно, она имеет лишь тривиальное решение, т.е. линейная комбинация λ₁a+λ₂b+λ₃c = 0 только при λ₁=λ₂=λ₃=0. Значит, система элементов {a, b, c} линейно независима.

Задача 3. По матрице Т=(t_ij) перехода от базиса A={a₁, a₂, a₃, a₄} к базису B={b₁, b₂, b₃, b₄}, элементы которых заданы в естественном базисе пространства R₄, найти координаты элемента a₂ в базисе C={b₂, b₃, b₁, a₄} и элемента b₄ в базисе А.

T =	2	-1	3	1
	1	1	-6	0
	4	0	5	0
	-3	0	0	0

Решение:

1) Имеем:

Значит,

2)

Тогда

Найдем :

Итак,

Тогда

и

Ответ: ,

Задача 4. Проверить, что система элементов a₁, a₂, a₃ евклидова пространства R⁵, заданных в естественном базисе со стандартным скалярным произведением, ортогональна. Дополнить исходную систему ортогональных элементов до ортогонального базиса.

a₁ = (1, 2, 0, 5, -1), a₂ = (3, 1, 7, -1, 0), a₃ = (-1, -2, 1, 2, 5)

Решение:

1) Если система элементов a₁, a₂, a₃ ортогональна, то эти элементы попарно ортогональны между собой, т.е. (a₁, a₂)=0, (a₁, a₃)=0, (a₂, a₃)=0.

Проверим это:

(a₁, a₂) = 3 + 2 – 5 = 0,

(a₁, a₃) = –1 – 4 + 10 – 5 = 0,

(a₂, a₃) = –3 – 2 + 7 – 2 = 0,

значит, система элементов a₁, a₂, a₃ ортогональна.

2) Пусть элементы a₄ и a₅ дополняют систему до ортогонального базиса. Найдем их, учитывая, что:

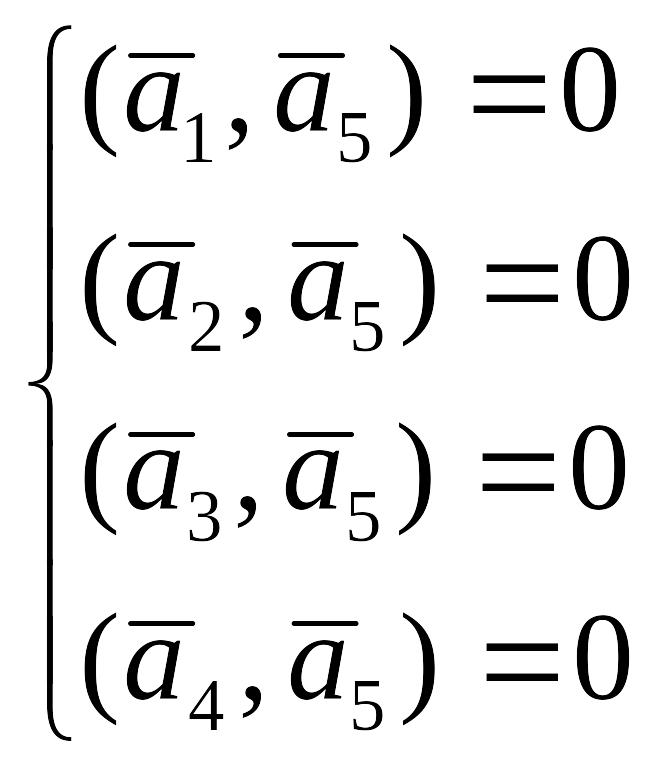(1) и (2)

Пусть . Распишем систему (1):

.

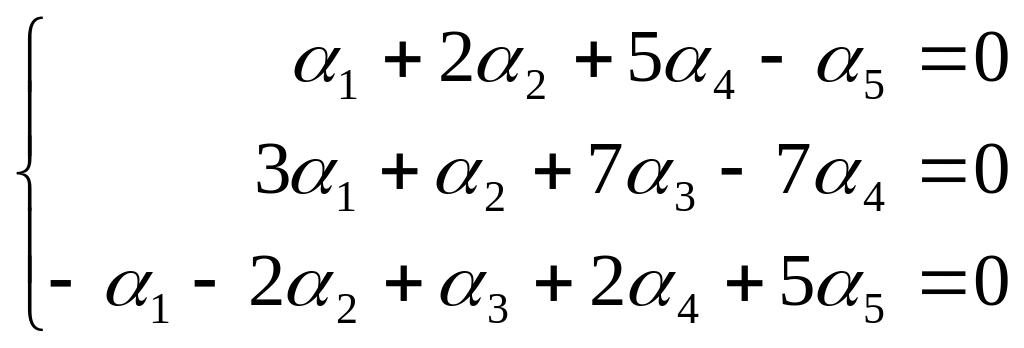
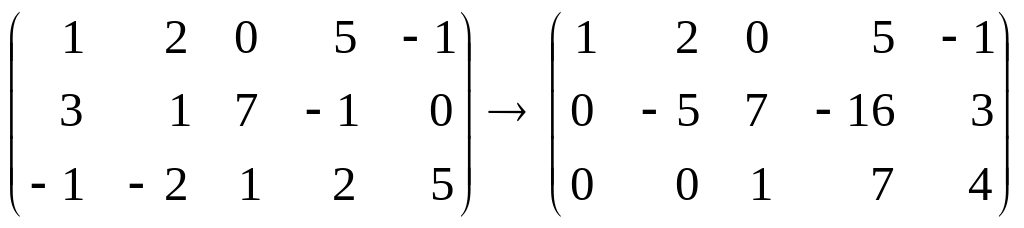Тогда

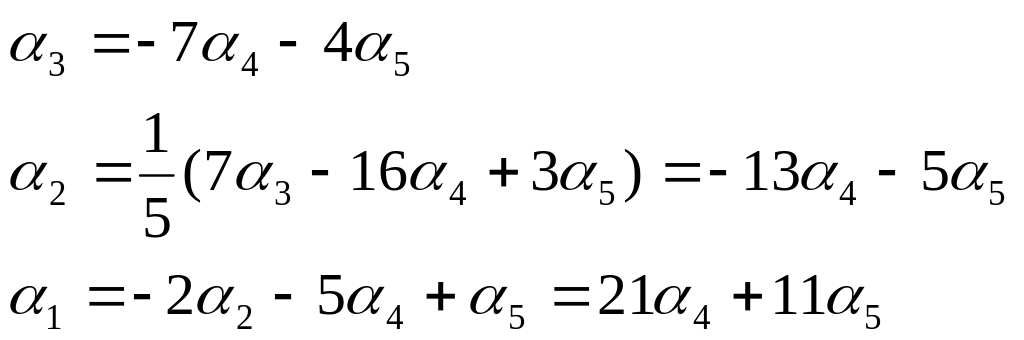
Пусть , тогда a₄ ( –1, –3, 1, 1, –2). (3)

3) Найдем координаты элемента a₅, учитывая (2) и (3).

Пусть . Тогда:

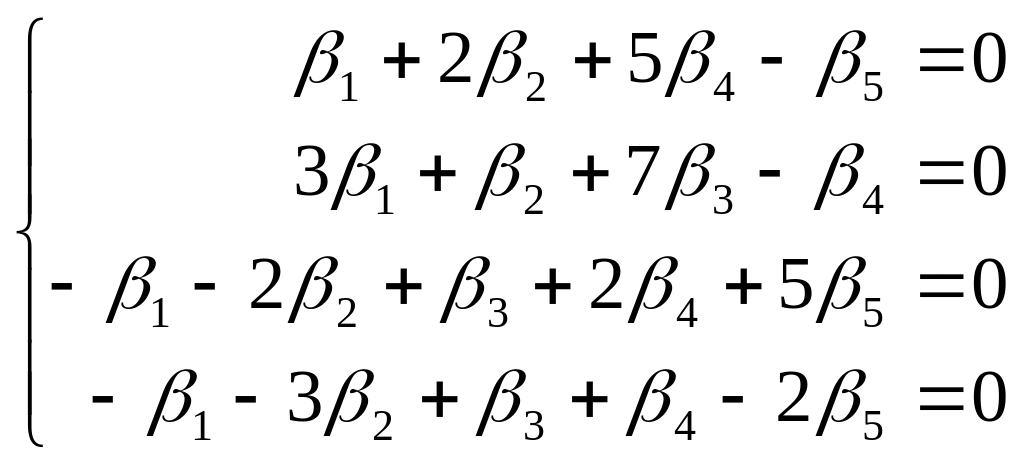
Имеем

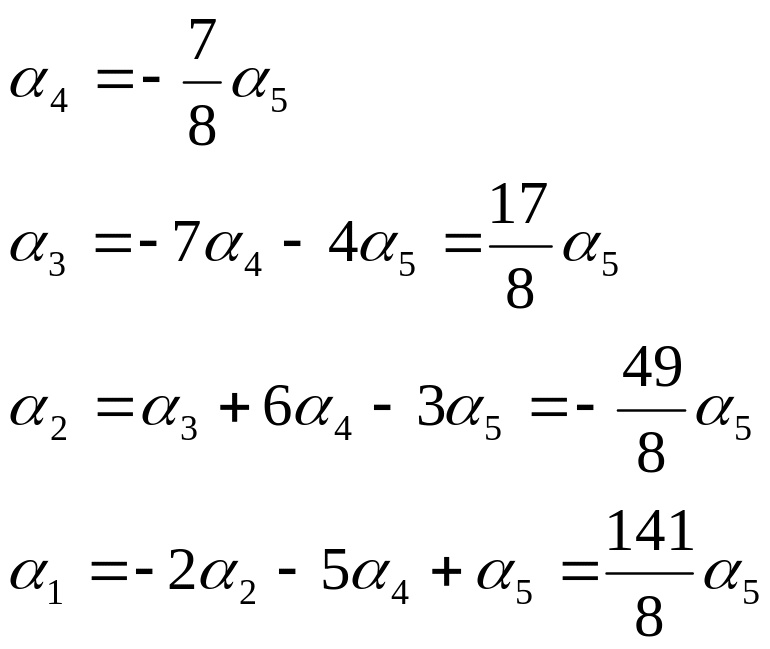
Пусть , тогда a₅ ( 141, –49, 17, –7, 8).

Ответ: a₄ ( –1, –3, 1, 1, –2), a₅ ( 141, –49, 17, –7, 8).

Задача 5. Выяснить, являются ли линейными операторами соответствующих пространств R^k операторы A₁, A₂, переводящие всякий элемент x = (x₁, x₂, …, x_k) пространства R^k в элемент y = (y₁, y₂, …, y_k), заданный координатами в том же базисе, что и x. Для линейных операторов найти их матрицы в том же базисе, где заданы элементы x и y. Вычислить ранг и дефект линейных операторов.

A₁(x)=(7x₁+6x₂–x₃+3x₄, 5x₁–4x₂+x₃–2x₄, 3x₁+2x₂, x₁)

A₂(x)=(5x₁+4x₂–x₃, –2x₂+3x₃, 3x₁+2x₂+2x₃–1)