
I. Линейная алгебра.
Задача 1. Даны матрицы А и В:
![]() ,
,
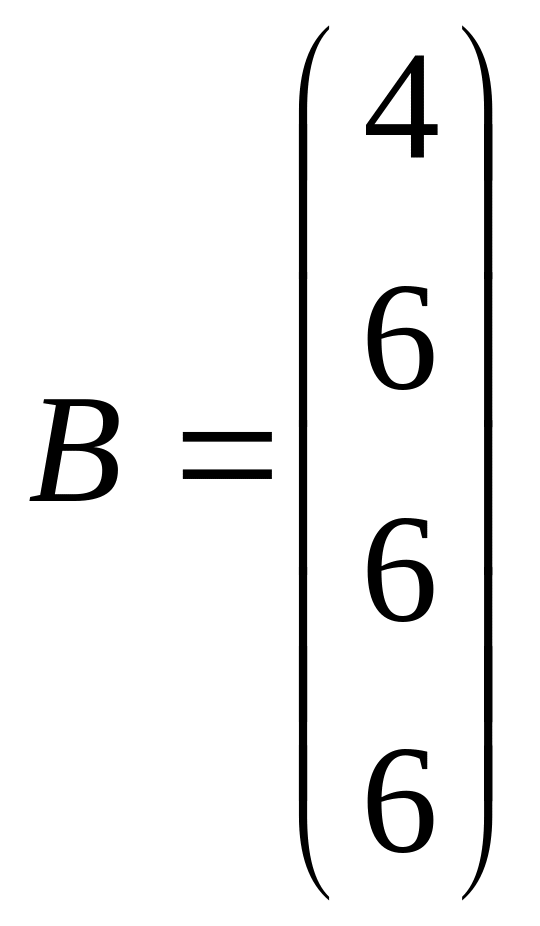
1. Найти матрицу А-1, обратную для матрицы А:
а) с помощью элементарных преобразований
б) с помощью алгебраических дополнений
2. Решить матричное уравнение АХ=В
РЕШЕНИЕ:
1. а)
![]()

Проверка:
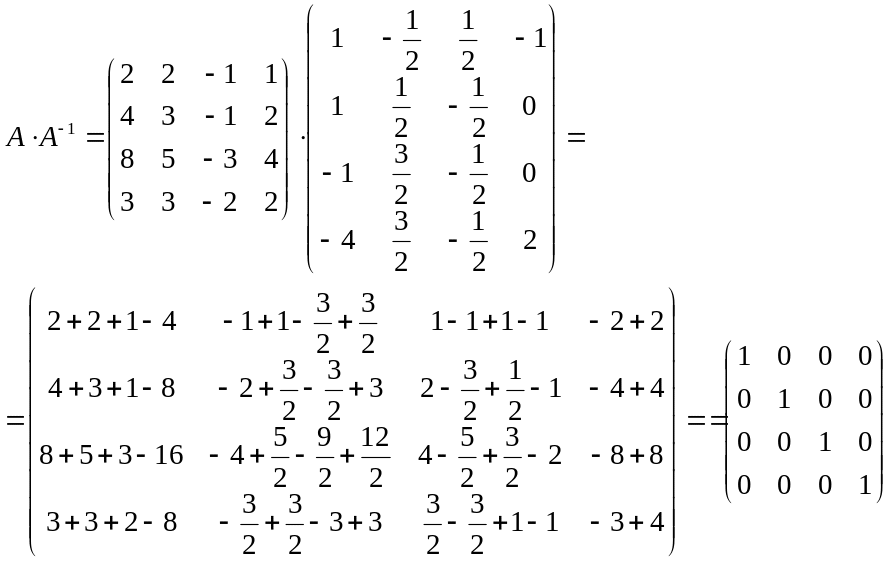
Обратная матрица была найдена верно.
б)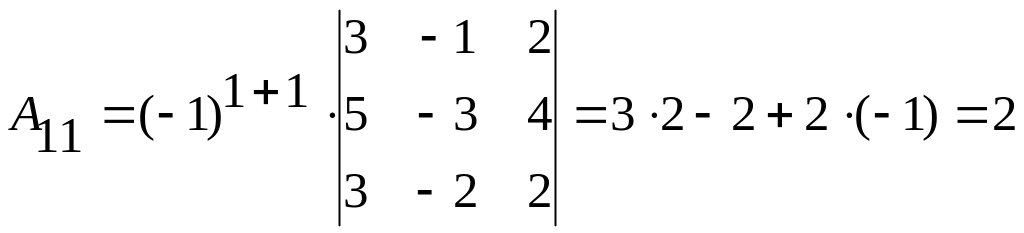
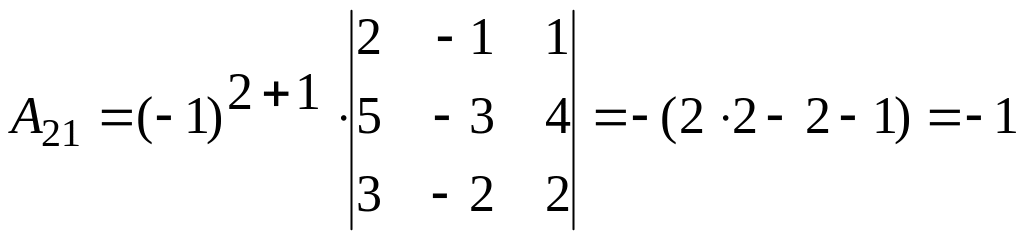
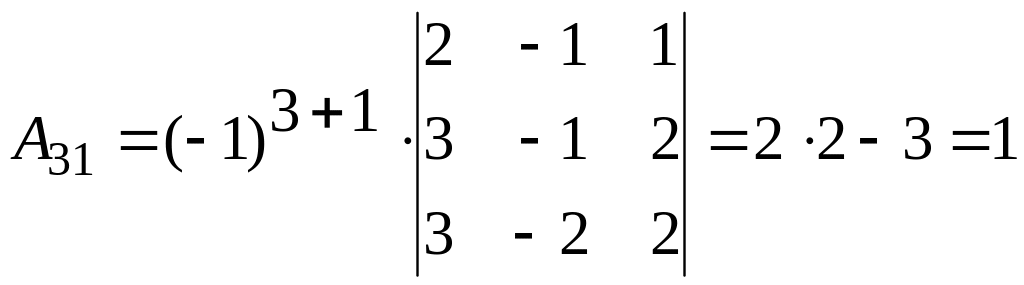
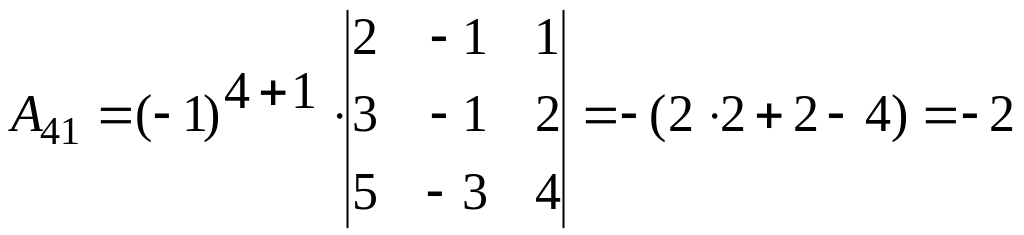
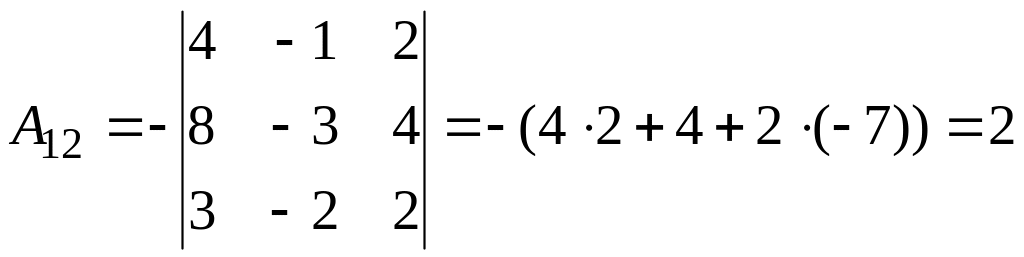
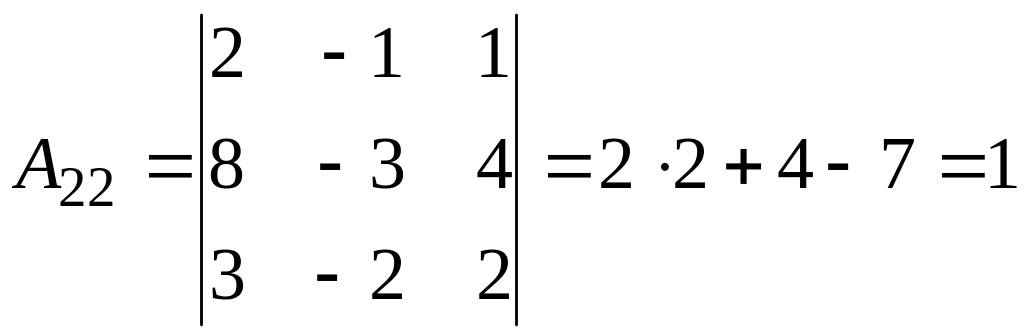
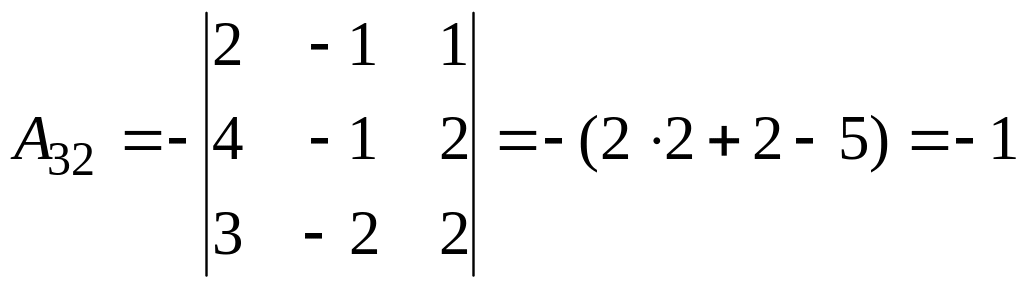
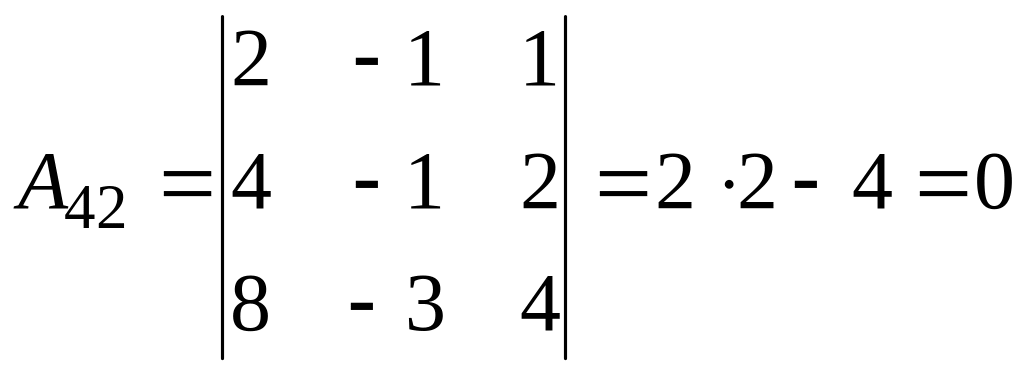
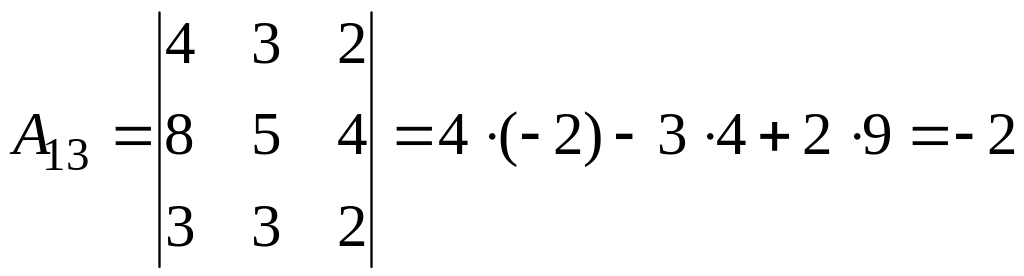
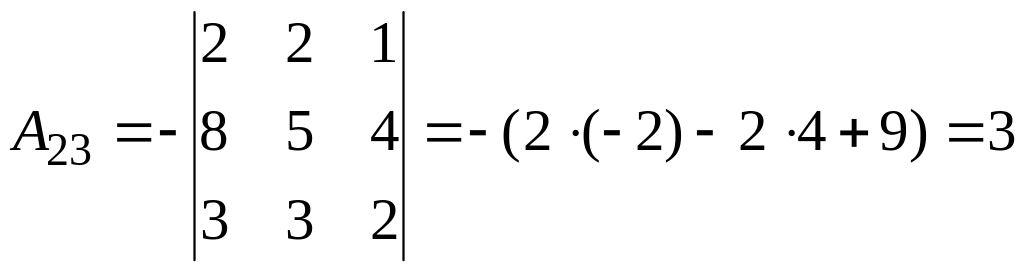

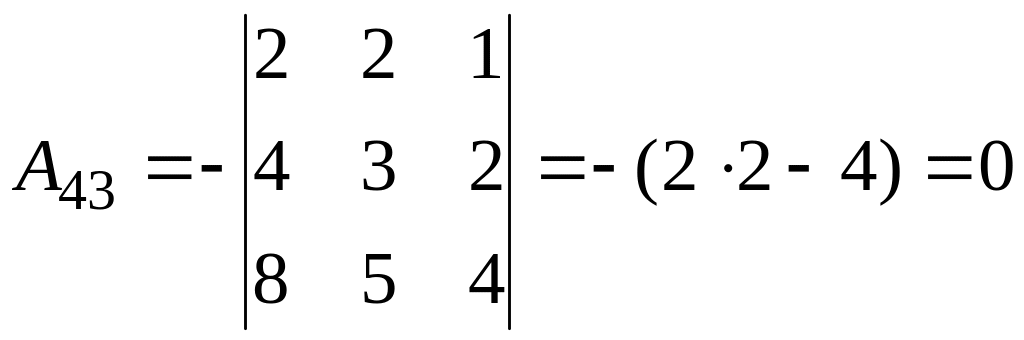
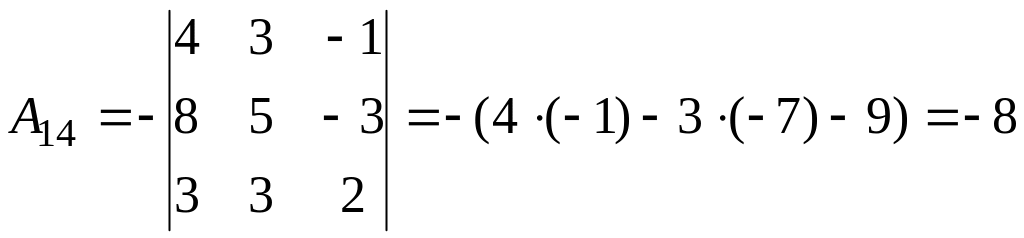
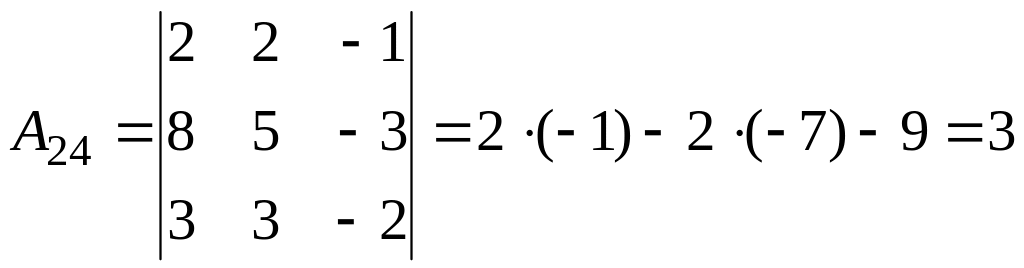
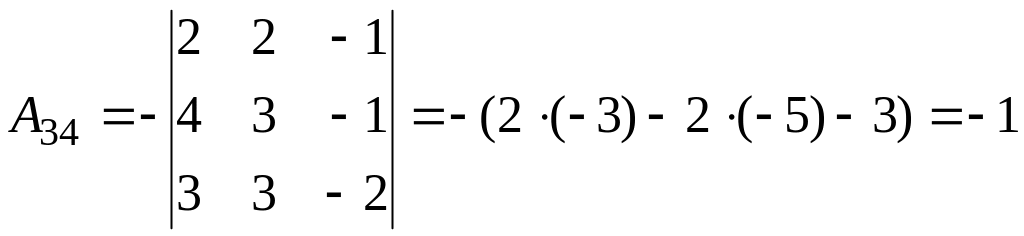
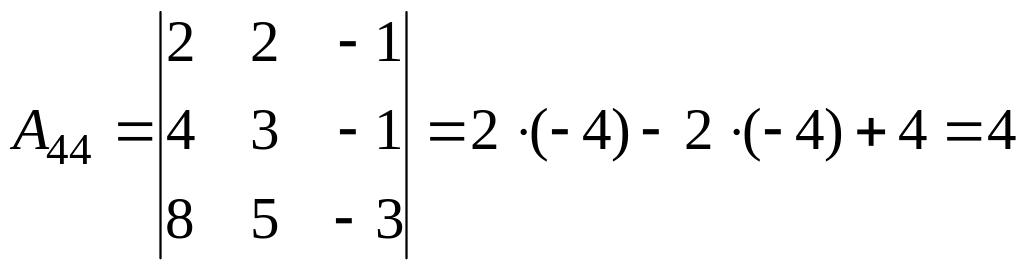
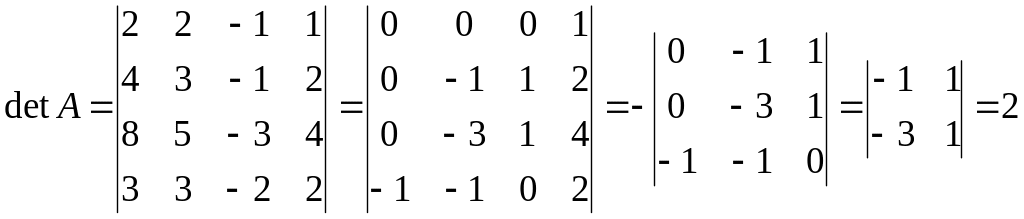
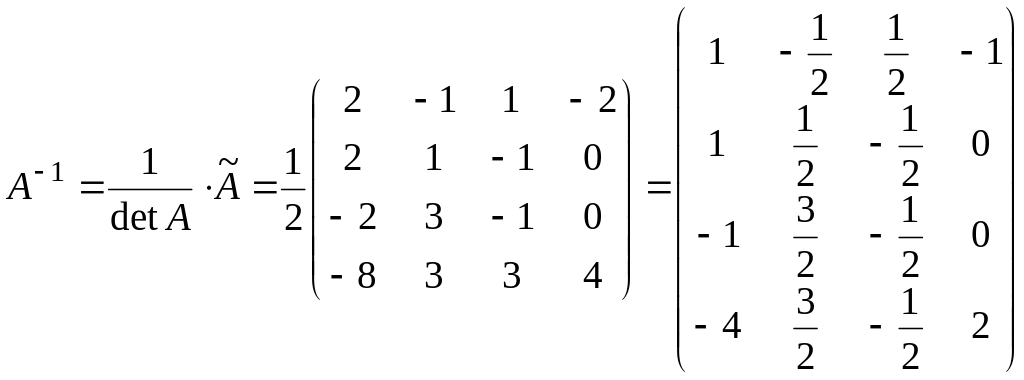
2.
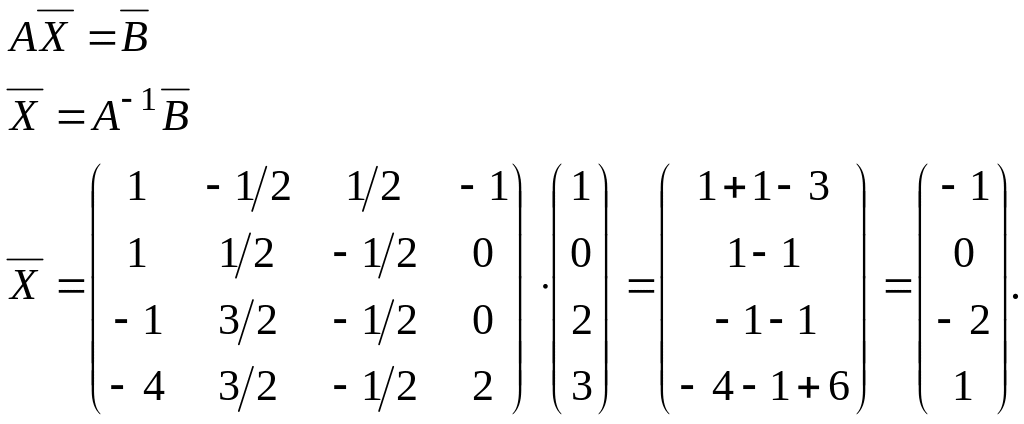
Ответ:
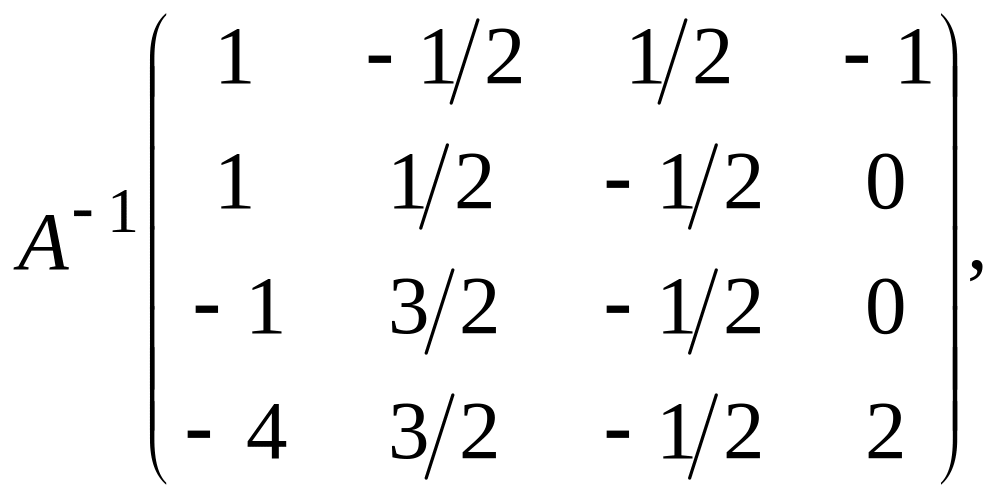
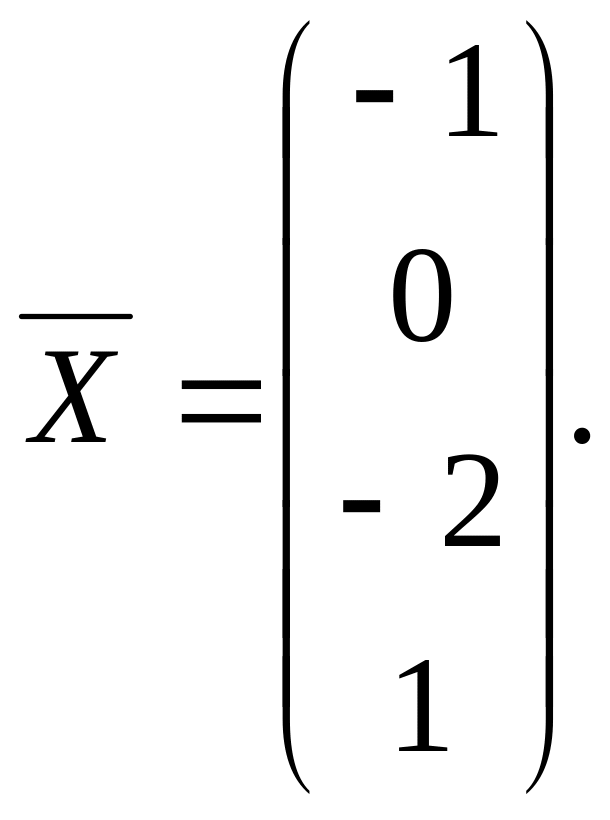
Задача 2. Найти значение многочлена f(x)=2x2–x+1 от матрицы А.
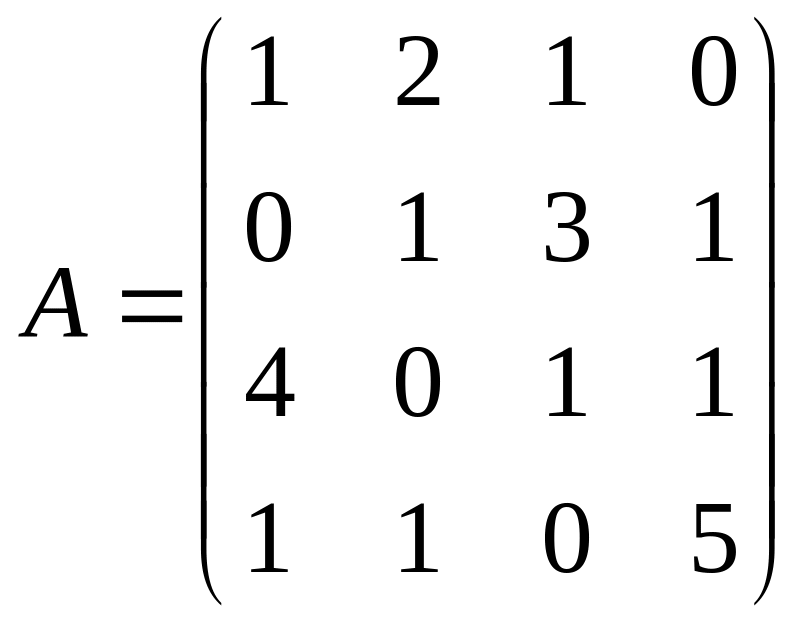
РЕШЕНИЕ:
1)
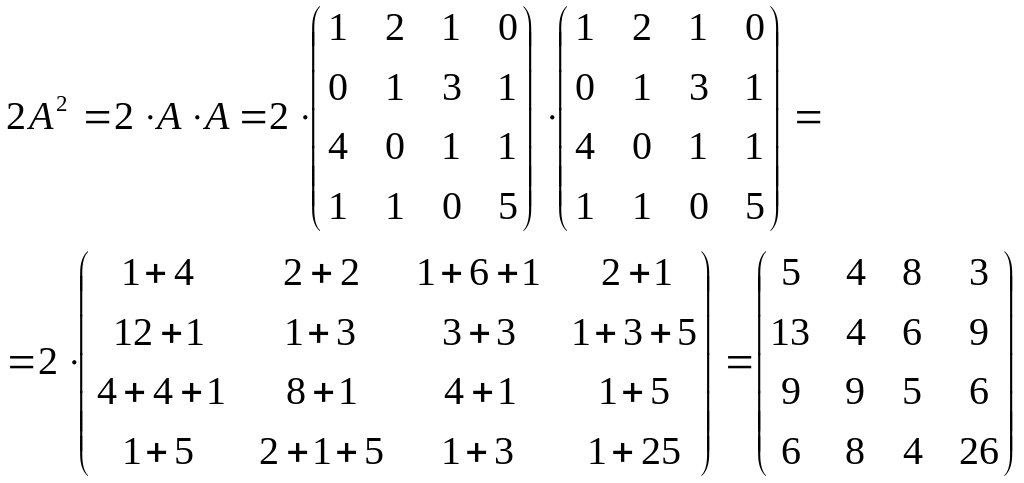
2)
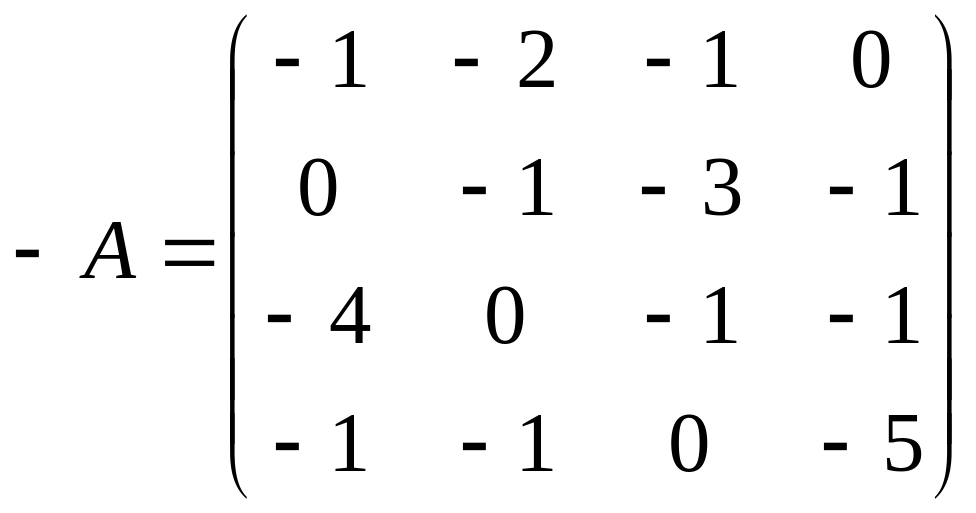
3)
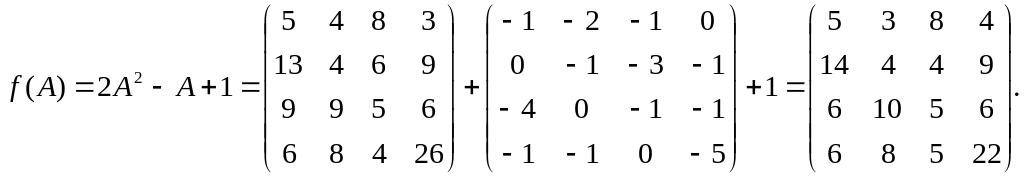
Ответ:

Задача 3. Решить уравнение над полем комплексных чисел
x2 - (4-6i)x + (10-20i) = 0
РЕШЕНИЕ:
1)
![]()
![]()
2)
![]() ,
где
k=0;
1.
,
где
k=0;
1.
3)
Пусть
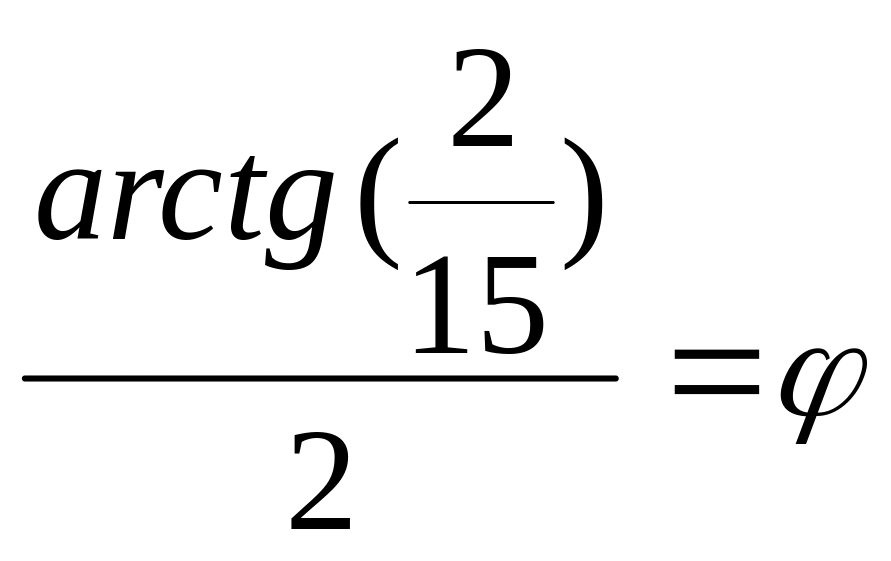 ,
где
,
где
![]() .
Тогда
.
Тогда
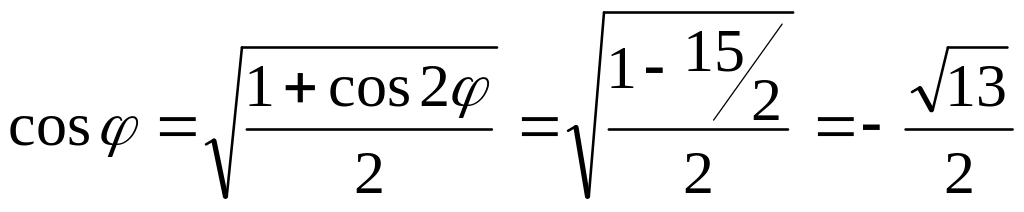
![]()
Таким
образом, при k=0
![]() .
Тогда
.
Тогда
![]()
![]()
Если
k=1,
то
![]() и
и
![]()
![]()
Ответ:
![]() ,
,
![]()
Задача 4. Решить систему уравнений над полем комплексных чисел:
 2x
+ (1+i)y
= 1-i,
2x
+ (1+i)y
= 1-i,
ix - 3y = 2i.
РЕШЕНИЕ:
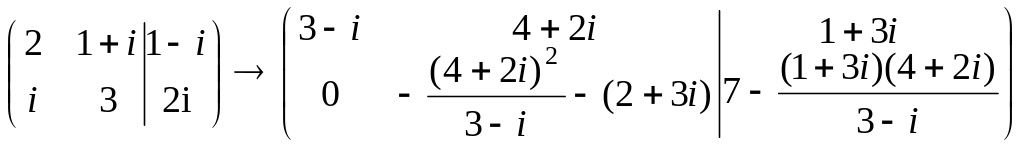
![]()
![]()
![]()
Ответ: (1, i)
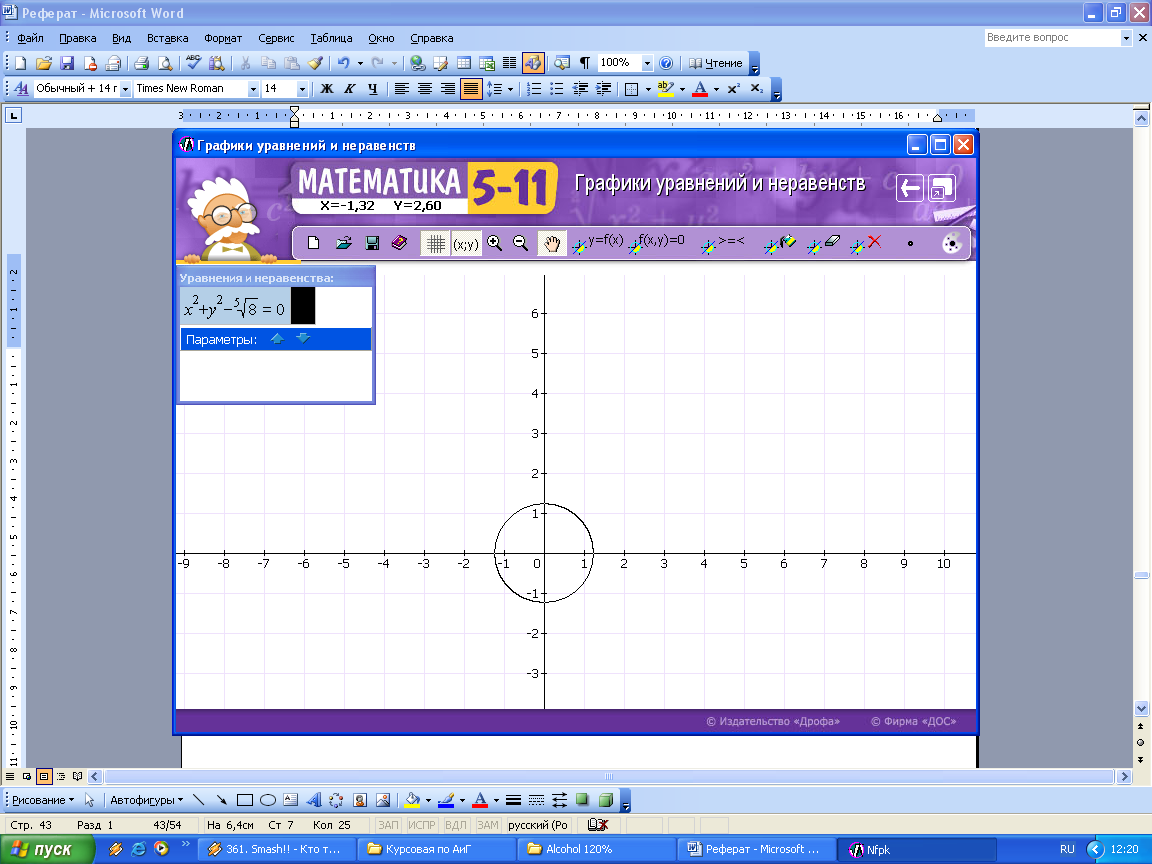
Задача 5. Найти все значения корней и изобразить их на плоскости.
![]()
РЕШЕНИЕ:
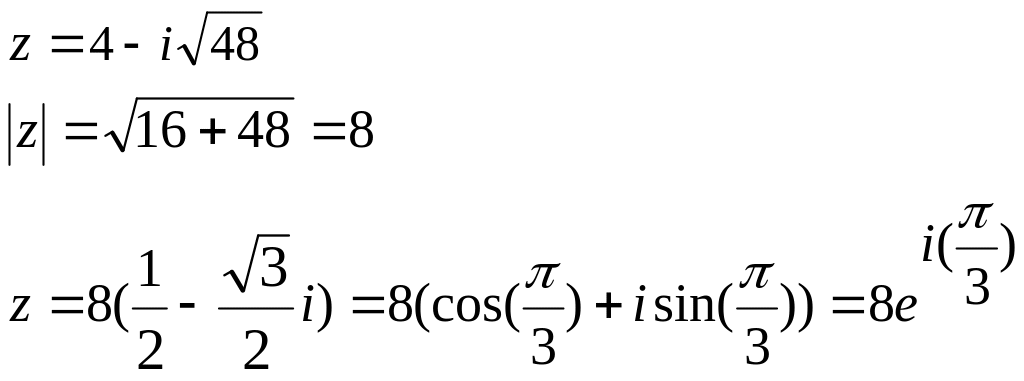
Тогда
![]() ,
где k=0,
1, 2, 3, 4.
,
где k=0,
1, 2, 3, 4.
Если
k=0,
то
![]()
Если
k=1,
то
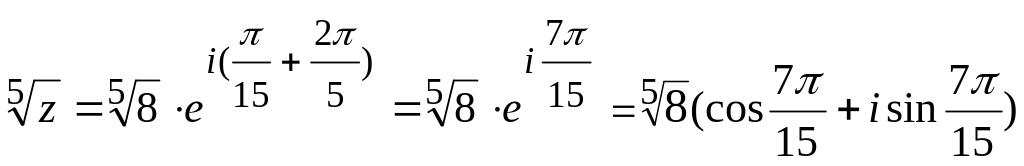
Если
k=2,
то
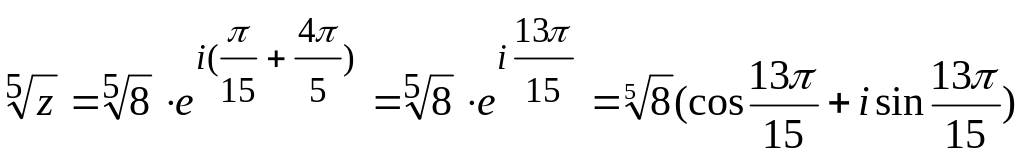
Если
k=3,
то
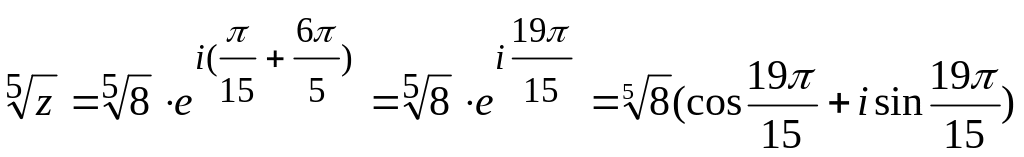
Если
k=4,
то
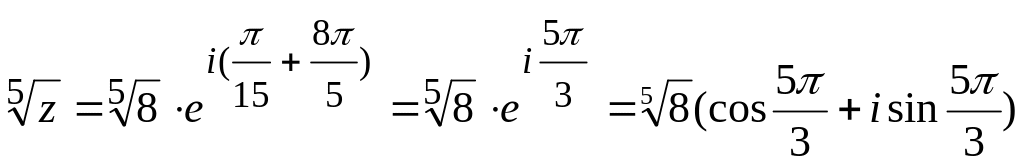
Задача 6. Исследовать систему линейных уравнений на совместность и решить ее. Найти общее и два любых частных решений.
-
x
 1
1+
x2
+
x3
+
x4
+
x5
=
5,
2x1
+
3x2
+
x3
+
x4
–
3x5
=
4,
x1
+
2x3
+
2x4
+
6x5
=
11,
x1
+
2x2
–
4x5
=
-1
Решение:
1) Найдем ранг матрицы системы:
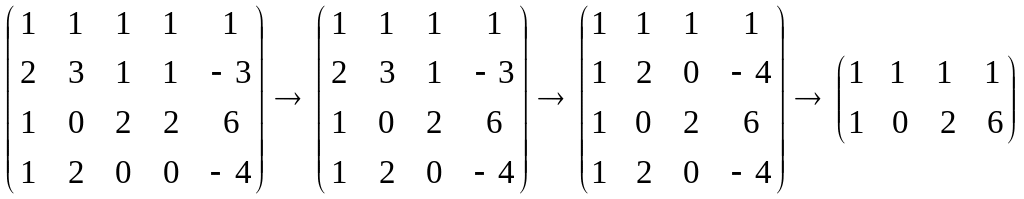
Rg(A)=2.
2) Найдем ранг расширенной матрицы:
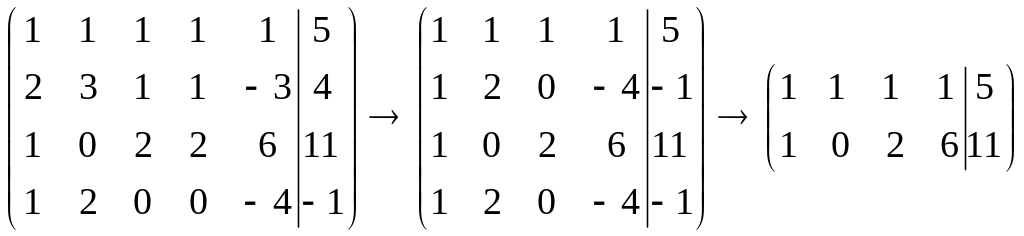
Rg(![]() )=2.
)=2.
3) Rg(A) = Rg( ), значит, система совместна, и в ней лишь два уравнения являются линейно независимыми. Запишем укороченную систему:
-
x
 1
1+
x2
+
x3
+
x4
+
x5
=
5
x1
+
2x3
+
2x4
+
6x5
=
11
Пусть x1 и x2 – базисные переменные, а x3 = с1, x4 = с2, и x5 = с3 – свободные. Тогда
-
x1
+
x2
=
5
–
с1
–
с2
–
с3,
x2
=
11
–
2с1
–
2с2
–
6с3.
![]()
Имеем общее решение:
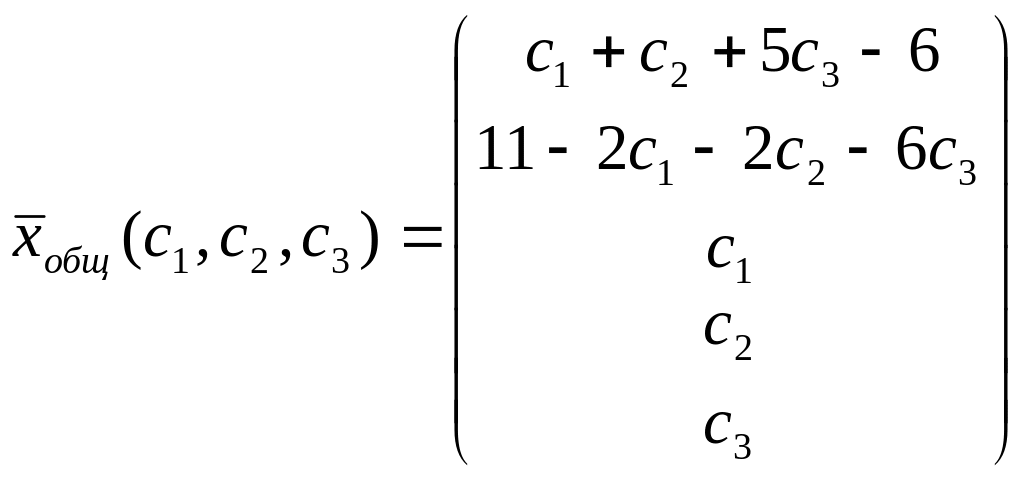
Пусть
с1=0,
с2=0,
с3=0,
то
![]()
Пусть
с1=1,
с2=1,
с3=1,
то
![]()
Ответ:
,
![]() ,
,![]()
Задача 7. Найти общее и какую-либо фундаментальную систему решений однородной системы линейных уравнений.
x |
+ |
x2 |
+ |
x3 |
+ |
x4 |
+ |
x5 |
= |
0, |
-3x1 |
+ |
2x2 |
+ |
x3 |
+ |
x4 |
+ |
3x5 |
= |
0, |
6x1 |
+ |
x2 |
+ |
2x3 |
+ |
2x4 |
+ |
|
= |
0, |
-x1 |
+ |
4x2 |
+ |
3x3 |
+ |
3x4 |
+ |
5x5 |
= |
0. |
Решение:
Найдем ранг матрицы системы:

Ранг матрицы равен трем, следовательно, три из четырех уравнений системы являются линейно независимыми. Запишем укороченную систему:
-3x1 |
+ |
2x2 |
+ |
x3 |
+ |
x4 |
+ |
3x5 |
= |
0, |
6x1 |
+ |
x2 |
+ |
2x3 |
+ |
2x4 |
+ |
|
= |
0, |
-x1 |
+ |
4x2 |
+ |
3x3 |
+ |
3x4 |
+ |
5x5 |
= |
0. |
Пусть x1, x2 и x3 – базисные переменные, тогда x4 = с1, и x5 = с2 – свободные. Имеем:
- |
+ |
2x2 |
+ |
x3 |
= |
с1 |
- |
3с2 |
6x1 |
+ |
x2 |
+ |
2x3 |
= |
–2с1 |
|
|
-x1 |
+ |
4x2 |
+ |
3x3 |
= |
–3с1 |
– |
5с2 |
Решаем полученную систему уравнений методом Гаусса:
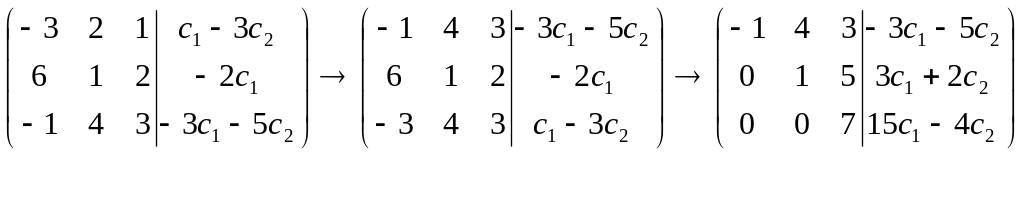
Имеем:

Итак, общее решение:
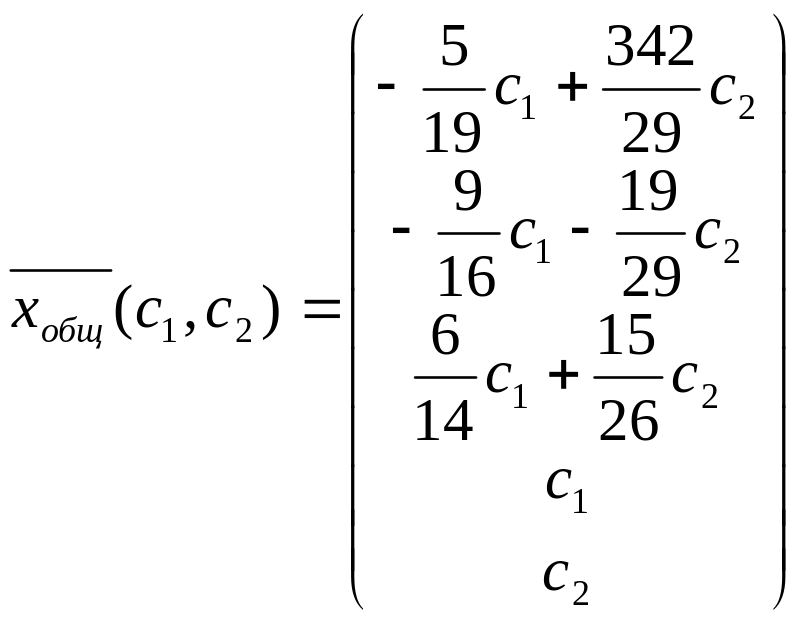
или
![]() ,
где
,
где
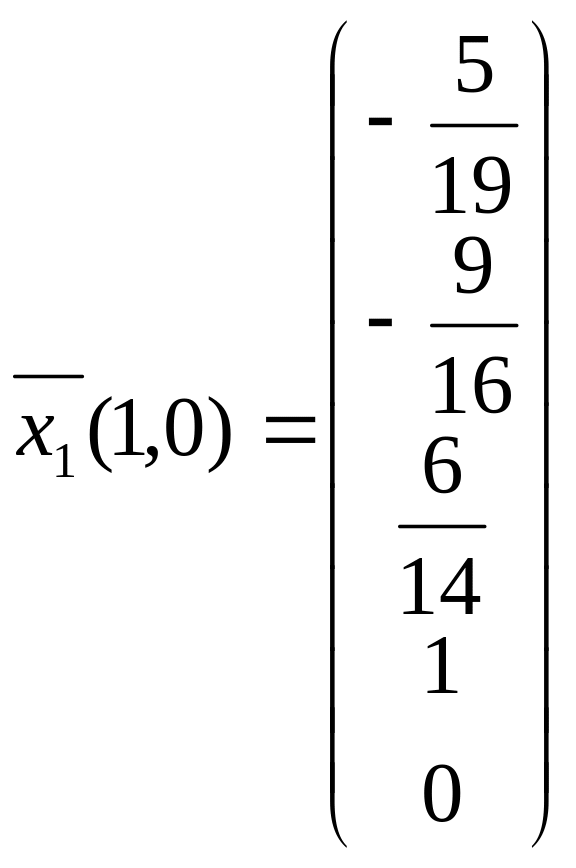 и
и
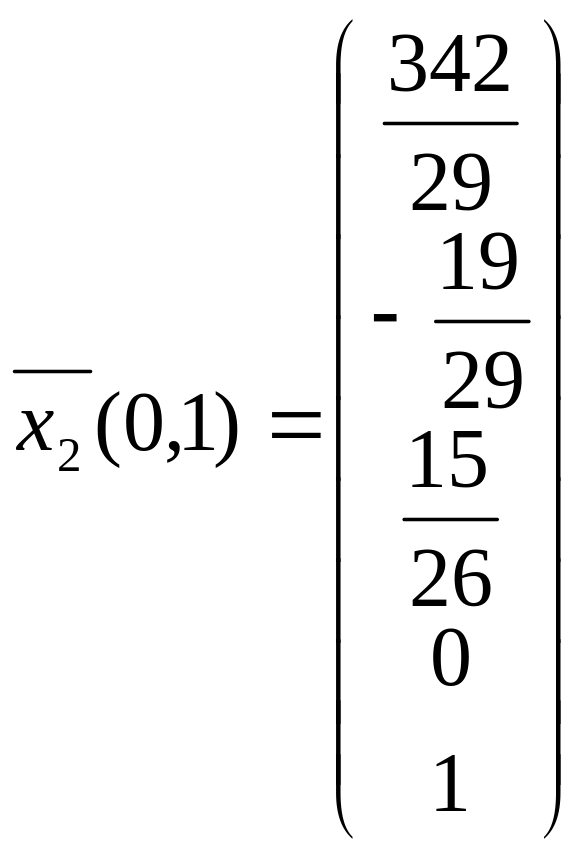 .
.
Ответ:
,
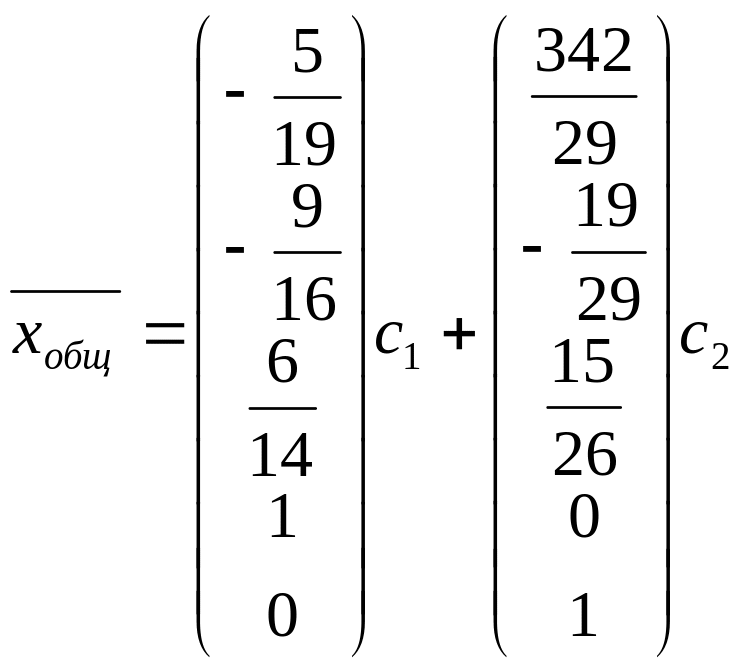

 1
1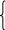 3x1
3x1