Тема. Додавання цілих невід’ємних чисел

План

1. Теоретико-множинний смисл суми двох цілих невід’ємних чисел.

2. Існування суми, її єдиність.

3. Сума декількох доданків.

4. Закони додавання.

1. Теоретико-множинний смисл суми двох цілих невід’ємних чисел

Розглянемо дві задачі.

1) «На тарілці лежать 3 груші і 5 яблук. Скільки всього фруктів на тарілці?»

Задача розв’язується виразом на додавання 3 + 5 = 8, бо мова йде про об’єднання двох множин: множини груш (число елементів – 3) та множини яблук (число елементів – 5). Ці множини не перетинаються. Щоб знайти, скільки всього фруктів на тарілці, треба об'єднати множини груш та яблук і полічити, скільки всього елементів у цьому об’єднанні. Число елементів об’єднання даних множин дорівнює 8; тобто 8 фруктів на тарілці.

2) «Знайти кількість елементів в об’єднанні множин A = {k, l, m, n} та B = {n, o, p}».

Розв’язання. Кількість елементів множини A: n (A) = 4, а кількість елементів множини B: n (B) = 3. За означенням A B = {k, l, m, n, o, p} n(A B) = 6. Але n (A B) ≠ 4 + 3. Чому? Тому, що А В = {n} і, отже,

n (A) + n (B) ≠ n (A B).

Звідси, суму цілих невід’ємних чисел визначають через об’єднання двох множин, що не перетинаються.

Означення. Сумою двох цілих невід’ємних чисел а і b називається число елементів в об’єднанні множин А і В, які не перетинаються і таких, що n (А) = а, п (В) = b, тобто а + b = п (А В), де а = п (А), b = п (В), А В = .

Сума не залежить від вибору двох множин, що не перетинаються, але таких, що n (A) = a і n (B) = b.

Приклади:

1) A = {a, b}, B = {c, d} A B = {a, b, c, d} і А В = , отже, n (A B) = n (A) + n (B) = 2 + 2 = 4, де n (A) = 2, n (B) = 2.

2) A = {Δ, Δ}, B = {Ο, Ο} A B = {Δ, Δ, Ο, Ο} і А В = , отже, n (A B) = n (A) + n (B) = 2 + 2 = 4, де n (A) = 2, n (B) = 2.

Дія, за допомогою якої знаходять суму, називається додаванням. Числа, які додаються, називаються доданками.

У початковому курсі математики додавання цілих невід’ємних чисел вводиться на основі виконання практичних вправ, пов’язаних з об’єднанням двох множин предметів (без використання відповідної символіки та термінології). Основним засобом розкриття теоретико-множинного смислу додавання є розв’язування простих текстових задач.

2. Існування суми, її єдиність

Теорема: «Сума цілих невід’ємних чисел завжди існує і вона єдина».

(Доведення теореми випливає з теореми про існування і єдиність операції об'єднання множин).

Іншими словами, які б не було взято два цілих невід’ємних числа а і b, завжди можна знайти їх суму – ціле невід’ємне число с, яке і буде єдиним для заданих чисел а і b.

2. Сума декількох доданків

Нехай сума двох доданків визначена і визначена сума п доданків. Тоді сума, що складається з n+1 доданка, тобто сума а₁ + а₂ + ... + а_п + а_п+1 дорівнює (а₁ + а₂ + ... + а_п) + а_п+1, тому

а₁ + а₂ + ... + а_п + а_п+1 = (а₁ + а₂ + ... + а_п) + а_п+1.

Приклад: .

2. Закони додавання

• Комутативний (переставний) закон: «Для будь-яких цілих невід’ємних чисел а і b виконується рівність: а + b = b + а.»

Доведення. Нехай а – кількість елементів множини A, b – кількість елементів множини B, тобто n(A) = а, n(B) = b і А В = . Тоді за означенням суми цілих невід’ємних чисел а + b = n (A B). А так як A B = B A (за комутативним законом об’єднання множин), то n (A B) = n (B A) за означенням суми n (B A) = b + а а+b = b+а для будь-яких цілих невід’ємних чисел.

• Асоціативний (сполучний) закон: «Для будь-яких цілих невід’ємних чисел а , b, с виконується рівність: (a + b) + с = а + (b + с)».

Доведення. Нехай а – кількість елементів множини A, b – кількість елементів множини B, с – кількість елементів множини С, тобто n (A) = а, n (B) = в, n (С) = с, А В = , B С = . Тоді за означенням суми двох цілих невід’ємних чисел (а + b) + с = n (A B) + n (C) = n ((A B) C). Так як за асоціативним законом об’єднання множин (A B) С = =A (B C), то n ((A B) С) = n (A (B C)) за означенням суми двох чисел n (A (B C)) = n (A) + n (B C) = а + (b + с) (а + b) + + с = а + (b + с).

• Властивість монотонності додавання: «Для будь-яких цілих невід’ємних чисел а , b, m таких, що а = b виконується рівність: ».

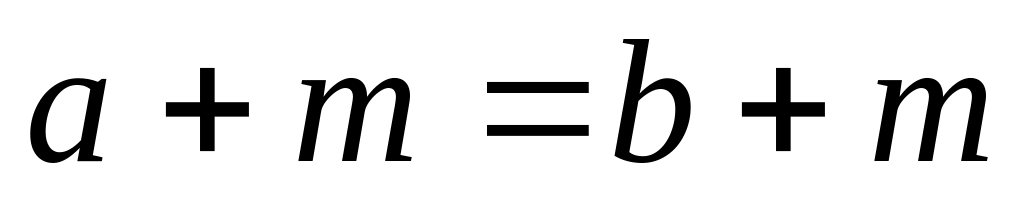Наслідки із комутативного та асоціативного законів додавання:

• Додавання числа до суми і суми до числа.

1) (а + b) + с = (а + с) + b = а + (b + с);

2) а + (b + с) = (а + b) + с=^:(а + с) + b.

Додати число до суми або суму до числа можна двома способами: обчислити суму і до результату додати дане число або додати це число до одного з доданків, а до результату додати другий доданок.

• Додавання суми до суми.

(а + b) + (с + d) = (а + с) + (b + d) = (а + d) + (b + с).

Для того щоб додати суму до суми, можна до одного з доданків першої суми додати один із доданків другої, а до другого доданку першої суми – інший доданок другої суми і одержані результати додати.

Ці правила легко поширити на будь-яку кількість доданків і об’єднати їх одним правилом: якщо при додаванні маємо дужки, то їх можна опустити і об’єднати між собою доданки в будь-якій послідовності так, щоб обчислення виконувати найзручнішим способом.

Із законами дії додавання учні початкових класів знайомляться поступово: спочатку вивчають переставну властивість додавання (1 клас), яка використовується при складанні таблиць додавання одноцифрових чисел, а далі для розкриття прийомів додавання та раціоналізації обчислень. В 4 класі при узагальненні і систематизації знань про дію додавання закони – переставний і сполучний формулюються та записуються у буквеному вигляді.