
- •3.1. Эпюра изгибающего момента
- •Процедура построения ординат эпюры
- •Правило знаков для ординат эпюр
- •Построение эпюры М на элементе стержня свободном от нагрузки
- •Процедура построения ординат эпюры Q
- •для бесконечно малого элемента
- •Признаки правильного вида эпюры Q
- •Пример построения эпюры Q по эпюре М
- •3.3. Эпюра продольных сил
- •Процедура построения ординат эпюры
- •Признаки правильного вида эпюры
- •3.4. Используемые способы контроля построенных эпюр
3. ПРАВИЛА ПОСТРОЕНИЯ ЭПЮР ВНУТРЕННИХ УСИЛИЙ M ,Q, N
3.1. Эпюра изгибающего момента M
Процедура построения ординат эпюры M
Для построения ординаты эпюры M в каком |
либо сечении стержня |
|
необходимо выполнить следующие две операции. |
|
|
1. С помощью уравнения равновесия |
∑M = 0 |
для левой отсеченной |
|
слева |
|
части стержневой системы (или ∑M = 0 |
для правой части) подсчитать |
|
справа |
|
|
численное значение изгибающего момента в сечении.
2. Отложить найденное численное значение в виде ординаты перпендикулярно оси стержня со стороны растянутого волокна стержня.
Численное значение изгибающего момента в сечении равно численному значению алгебраической суммы моментов всех сил, действующих на стержневую систему с любой одной из сторон сечения, взятых относительно точки на оси сечения.
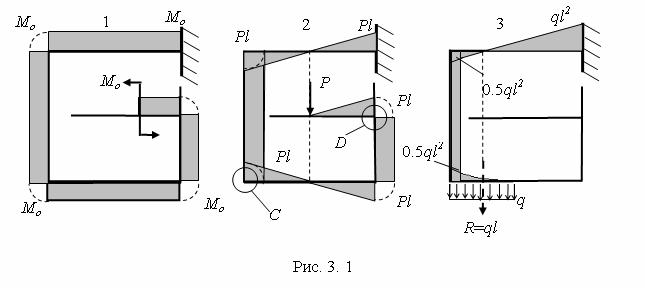
Как устанавливается растянутое волокно в сечении, продемонстрировано на примере консоли ломаного очертания при ее загружении тремя видами нагрузки (рис. 3.1). Ординаты соответствующих трех эпюр M построены на растянутой стороне стержней, образующих консоль.
Признаки правильного вида эпюры M
При указанном правиле построения ординат эпюры M эта эпюра имеет следующие свойства.
44
1.На участке прямого стержня, свободном от нагрузки, эпюра прямолинейна.
2.На участке распределенной нагрузки она очерчена кривой линией, выпуклой в сторону действия нагрузки. Когда нагрузка равномерно распределена, кривая является параболой второй степени.
3.В точке приложения сосредоточенной силы эпюра имеет излом, острие которого направлено в сторону действия силы.
4.В точке приложения сосредоточенного момента эпюра имеет скачок в ординатах, равный величине момента.
5.В сечении, находящемся на границе незагруженного участка стержня и участка, загруженного распределенной нагрузкой, кривая линия эпюры плавно (без излома) переходит в прямолинейную эпюру, которая является касательной
ккриволинейному участку.
Эти свойства используют для контроля построенных эпюр M .
Правило знаков для ординат эпюр M
При построении ординат эпюры M со стороны растянутого волокна стержня вручную, знак ординаты не требовался. Однако при численном расчете на ПК, каждой ординате эпюры M присваивается знак. Используется знак эпюры M и при построении по ней эпюры Q .
В данном учебном пособии приводится правило знаков, принятое для ординат эпюр M в программе SCAD [2 − 5].
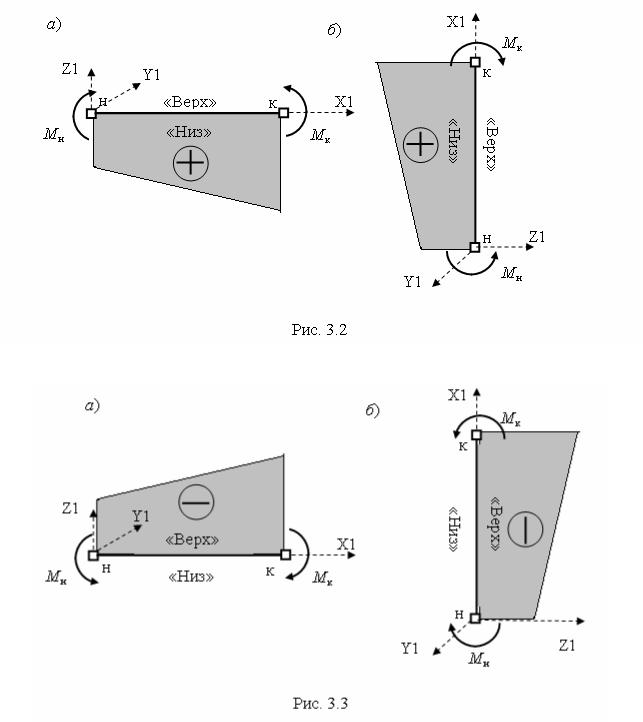
Если растянуто «нижнее» волокно стержня, то ордината откладывается от оси стержня «вниз» и ей присваивается знак «+»
(рис. 3. 2).
Если же растянуто «верхнее» волокно стержня, то ордината откладывается от оси стержня «вверх» и ей присваивается знак « – » (рис. 3.3).
«Нижним» волокном стержня в программе SCAD считается волокно стержневого конечного элемента (КЭ) типа «Стержень плоской рамы», находящееся со стороны отрицательных ординат оси Z1 местной системы осей координат (МСК), а «верхним» – со стороны положительных ординат оси Z1 (см. рис. 3.2, 3.3).
Примечание. При ручном подсчете алгебраической суммы моментов всех сил с одной стороны от сечения для определения изгибающего момента в сечении стержня, рекомендуется сразу ставить знаки слагаемых моментов в соответствии с этим правилом знаков. Тогда ордината изгибающего момента получится со своим знаком в соответствии с принятым правилом и может быть отложена от оси стержня по этому правилу.
45
Построение эпюры М на элементе стержня свободном от нагрузки
Из приведенных выше свойств эпюры M (признаков правильной эпюры)
известно, что если на конечном элементе стержня нет внешней нагрузки, то эпюра изгибающих моментов на нем будет прямолинейной. Для ее построения достаточно вычислить ординаты только в конечных сечениях такого элемента.
Примечание. В программе SCAD для получения ординат изгибающих моментов на КЭ загруженных распределенной нагрузкой «по умолчанию» может быть назначено вычисление для нескольких, например, трех сечений КЭ: в начале (н), в середине (с) и в конце (к) конечных элементов (начальное сечение «н» связано с началом оси X1 в МСК).
46
Тогда с целью сокращения выходных результатов для КЭ без нагрузки в их пределах
в разделе Назначения [2 − 5] на инструментальной панели необходимо нажать кнопку  «Назначение промежуточных сечений для расчета усилий». Откроется диалоговое окно «Вычисление усилий…..» (см. в программе SCAD справку к этому окну). В диалоговом окне на поле «количество сечений» вносится цифра 2. Далее надо закрыть окно и отметить конечные элементы на схеме стержневой системы, на которых ожидаются линейные эпюры M . Как это делается, показано в пособиях [2 − 5].
«Назначение промежуточных сечений для расчета усилий». Откроется диалоговое окно «Вычисление усилий…..» (см. в программе SCAD справку к этому окну). В диалоговом окне на поле «количество сечений» вносится цифра 2. Далее надо закрыть окно и отметить конечные элементы на схеме стержневой системы, на которых ожидаются линейные эпюры M . Как это делается, показано в пособиях [2 − 5].
На рис. 3.2, 3.3 концевые сечения стержня обозначены узлами « н » и « к » МСК. После назначения для расчета усилий в отмеченных элементах только двух сечений, в программе SCAD в соответствующей таблице усилий [2 − 5] будут выдаваться значения изгибающих моментов M н (M1) и M к (M 2 ) только в узлах «н» (1) и «к» (2) (со своими
знаками в МСК).
При оцифровке ординат эпюры моментов, которая выполняется при нажатии кнопки
 фильтра отображения, в пределах каждого конечного элемента из указанных двух моментов ( M1, M 2 ) приводится момент с максимальным значением.
фильтра отображения, в пределах каждого конечного элемента из указанных двух моментов ( M1, M 2 ) приводится момент с максимальным значением.
Построение эпюры М на элементе стержня при действии по его длине равномерно распределенной нагрузки
Если по всей длине КЭ расположена равномерно распределенная нагрузка, то эпюра изгибающих моментов на нем будет иметь вид параболы с выпуклостью направленной в сторону действия нагрузки.
Примечание. В программе SCAD с помощью процедуры, которая только что была рассмотрена по назначению для вычисления изгибающих моментов только в двух сечениях КЭ, можно назначить вычисление моментов в ряде сечений между узлами « н » и « к » элемента в МСК.
Для приближенного построения параболы достаточно вычислить ординаты эпюры M в трех сечениях КЭ: в начале «н», в середине «с» и в конце «к». В результирующей таблице усилий программы SCAD эти сечения обозначены соответственно 1, 2, 3. В программе SCAD вычисление моментов в указанных сечениях может быть обеспечено по умолчанию. Однако, если по какой-то причине у расчетчика оказались известными только две ординаты эпюры M по концам элемента ( M н и M к), то можно легко вычислить
ординату M c в среднем сечении, применив принцип независимости действия сил.
Пример. Вырежем (по узлам «н» (1) и «к» (3) МСК) из стержневой системы элемент, загруженный равномерно распределенной нагрузкой интенсивностью q (рис. 3.4,а).
Рассмотрим его, как балку на двух опорах, под действием внутренних усилий по концам элемента и распределенной нагрузки (рис. 3.4,б). Добавление указанных трех опорных связей не влияет на усилия в элементе, так как в вырезанном состоянии он находится в равновесии, поэтому в добавленных связях усилия (реакции) будут нулевыми.
Изгибающий момент M c в среднем сечении элемента (см. рис. 3.4, б) можно вычислить как сумму средней ординаты (рис. 3.4, в) линейной эпюры моментов (линии
47
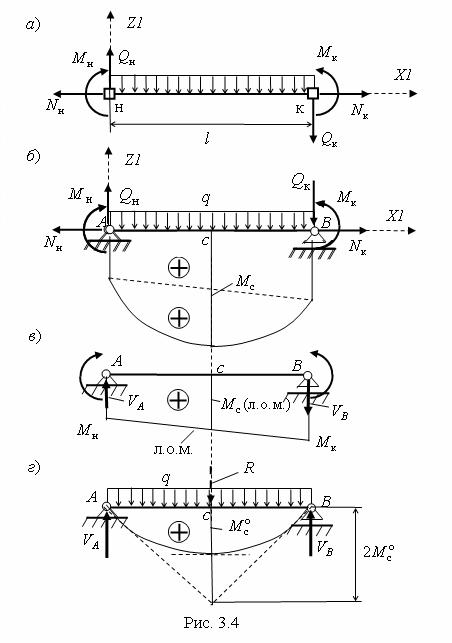
опорных моментов, или ЛОМ) M c (лом) = 0.5(M н +M к ) и средней ординаты Mco = ql2 / 8
параболической эпюры в простой балке на двух опорах от равномерно распределенной нагрузки (рис. 3.4, г):
M c =0.5(M н +M к ) +M co . |
(3.1) |
Обе суммируемые ординаты в рассмотренном примере положительны, так как они расположены снизу от оси балки. На рис. 3.5 показан вариант, когда ордината
M c (лом) =0.5(M н +M к ) отрицательна (ордината M co = ql 2 / 8 при указанном направлении нагрузки q положительна). Здесь же приведен графоаналитический способ построения параболической эпюры по трем ее суммарным ординатам ( M н, M с, M к ) и по трем
касательным к параболе в соответствующих концах ординат (отмечены крестиком).
Смысл этого графоаналитического способа будет понятен, если рассмотреть на рис. 3.4, г эпюру M (R) треугольной формы, показанную штриховыми линиями. Эпюра
48
