Расчетно-графическая работа №2. Вариант 10

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ

Расчетная графическая работа№2

Пространственная система сил

Вариант 10

Выполнил: студент группы ЭССН-202д Имамов Д.Д.

Проверил: преподаватель Сидоров В.Е.

г. Нефтекамск 2006

Задание: Прямоугольная однородная плита весом , на которую действует сила , удерживается в горизонтальном положении опорами , и невесомым стержнем . При этом сила не лежит в плоскости плиты (), а расстояние между опорами и равно . Определить реакции опор , и усилие в стержне .

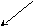
Дано: =200 H;

=100 H;

=0,5м;

=0,4м;

=0,35м;

=60;

=30.

Решение: Рассмотрим равновесие прямоугольной однородной плиты, вес которой приложен в точке пересечения диагоналей прямоугольника. Отбросим связи, которыми являются опоры , и невесомый стержень , заменяя их действие реакциями .

Так как реакция опоры может иметь любое направление в пространстве, то заменяем ее тремя взаимно перпендикулярными составляющими .

Опора допускает перемещение плиты вдоль оси . Поэтому ее реакцию, перпендикулярную оси , заменяем двумя взаимно перпендикулярными составляющими и . Реакцию невесомого стержня направим вдоль самого стержня.

Таким образом, плита находится в покое под действием активных сил , и реакций . Число неизвестных величин равно шести и совпадает с числом независимых уравнений равновесия, которые можно составить для рассматриваемой пространственной системы сил.

Переходя к составлению уравнений равновесия, заметим, что неизвестны углы, которые образуют сила с осями и . Поэтому разложим силу на две составляющие так, чтобы одна из них – , была направлена вдоль оси , а вторая – , лежала в плоскости . Модули этих составляющих определяются выражениями:

Учитывая, что составляющая составляет с осью угол , причем

составим уравнения проекций сил:

Перейдем к составлению уравнений моментов сил относительно оси . Так как линии действия сил пересекают ось , а сила параллельна этой оси, то моменты указанных сил относительно оси равны нулю. Поэтому:

Моменты сил относительно оси равны нулю, т. к. линии действия перечисленных сил пересекают ось . Следовательно,

Линии действия сил пересекают ось , а силы , параллельны этой оси. Значит, их моменты относительно оси равны нулю. Поэтому

Составим систему уравнений:

Отсюда найдем:

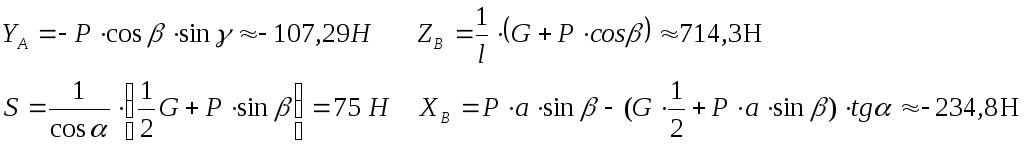
Подставив полученные значения в уравнения :

Тогда получим: