Расчетно-графическая работа №2. Вариант 5

Уфимский государственный авиационный технический университет

Кафедра теоретической механики.

Расчетно-графическая работа №2

«Кинематика точки и твердого тела»

1064 02 05 07 000

Выполнил: студент группы ИИТ-137

Зинатуллин И.Р.

Проверил: профессор Терешин В.Г.

УФА 2007

Задание №1(К1). Определение скорости и ускорения точки по заданным уравнениям её движения.

По заданным уравнениям движения точки М установить вид её траектории и для момента времени t=t₁(с) найти положение точки на траектории, её скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.

Данные:

Уравнения движения		t1, с
x=x(t), см	y=y(t), см
2sin(πt/3)	-3cos(πt/3)+4	1

t	x	y
0,00	0,00	1,00
0,10	0,21	1,02
0,20	0,42	1,07
0,30	0,62	1,15
0,40	0,81	1,26
0,50	1,00	1,40
0,60	1,18	1,57
0,70	1,34	1,77
0,80	1,49	1,99
0,90	1,62	2,24
1,00	1,73	2,50

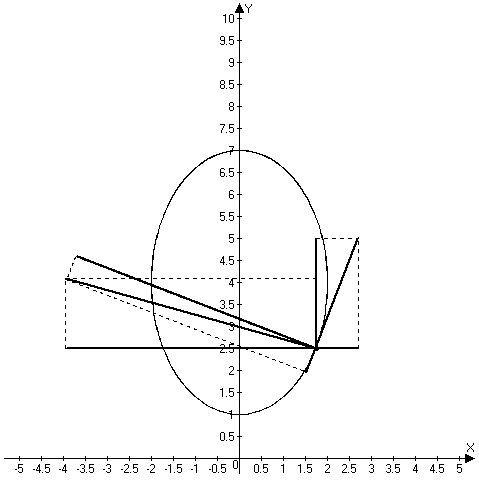
Решение:

x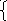=2sin(πt/3),

y=-3cos(πt/3)+4;

3x=6sin(πt/3),

-2y=6cos(πt/3)-8;

9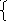x²=36sin²(πt/3),

(8-2y)²=36cos²(πt/3);

___

(8-2y)²=36-9x²; => y=(8-3√4-x²)/2;

_

x₁=2sin(π/3)=√3≈1,7(см);

y₁=-3cos(π/3)=2,5(см);

v_x=x= (2π/3) cos(πt/3);

v_y=y= π sin(πt/3);

v_x1=(2π/3) cos(π/3)= π/3≈1(см/с);

v_y1= π sin(π/3) 2,7(см/с);

______

v=√v_x²+v_y²≈2,9(см/с);

a_x=x=-(2π²/9) sin(πt/3);

a_y=y=(π²/3) cos(πt/3);

a_x1=-(2π²/9) sin(π/3)≈-5,7(см/с²);

a_y1=(π²/3) cos(π/3)≈1,6(см/с²);

______

a=√a_x²+a_y²≈5,9(см/с²);

a_τ= (v_xa_x+ v_ya_y)/v≈-0,5(см/с²);

a_n= (v_xa_y+ v_ya_x)/v≈5,9(см/с²);

ρ=v²/a_n≈1,4(см).

Результаты:

Координаты, см		Скорость, см/с			Ускорение, см/с2					Радиус кривизны,см
x	y	vx	vy	v	ax	ay	a	aτ	an	ρ
1,7	2,5	1	2,7	2,9	-5,7	1,6	5,9	-0,5	5,9	1,4

Задание №2(К2). Определение скоростей и ускорений точек и твердого тела при поступательном и вращательном движениях.

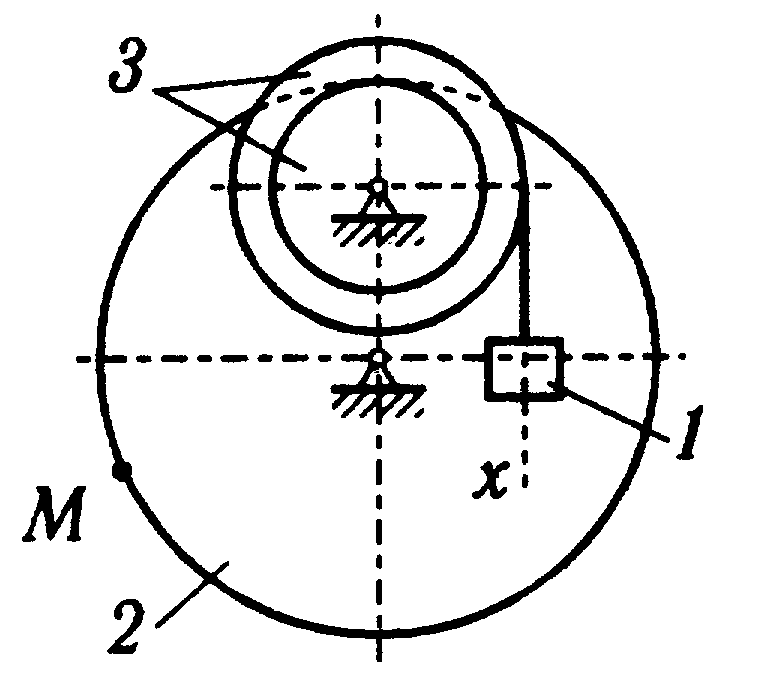
x

Движение груза описывается уравнением

x=c₂t²+c₁t+c₀,

где t-время, с; с₀,с₁,с₂-некоторые постоянные.

В начальный момент времени (t=0) положение груза определяется координатой x₀,и он имеет скорость v₀. Учесть, что в момент времени t=t₂ координата груза равна x₂.

Определить коэффициенты с₀,с₁ и с₂,при которых осуществляется требуемое движение груза 1. Определить также в момент времени t=t₁ скорость и ускорение груза и точки М одного из колес механизма.

Данные:

Радиусы, см				Координаты и скорости груза 1			Расчетные моменты времени, с
R2	r2	R3	r3	x0,см	v0,см/с	x2	t2	t1
80	-	45	30	3	15	102	3	2

Решение:

v=x=2c₂t+c₁; => c₁=15(см);

x=c₂t²+c₁t+c₀; => c₀=3(см);

x₂=c²t₂²+c₁t₂+c₀; => c₂=6(см).

Уравнение движения груза 1 имеет вид:

x=6t²+15t+3.

v=x=12t+15;

v=12∙2+15=39(см/с);

a=x=12(см/с²);

ω₃=v/R₃≈0,87(рад/с);

ε₃=ω₃≈0,27(рад/с²);

v_M=r₃ω₃=r₃v/R₃=26(см/с);

a^ц_М=r₃ω₃²≈22,5(см/с²);

а^в_М= r₃ε₃≈7,9(см/с²);

___________

а_М= √(а^в_М)²+(a^ц_М)²≈23,9(см/с²);

Результаты:

v, см/с	a, см/с2	ω3, рад/с	ε3, рад/с2	vM, см/с	aцМ, см/с2	авМ, см/с2	аМ, см/с2
39	12	0,87	0,27	26	22,5	7,9	23,9