Проверяем единицу измерения полученной величины

Пример 9. Тело вращается вокруг неподвижной оси по закону, выраженному формулой = 10 + 20t - 2t². Найти по величине и направлению полное ускорение точки, находящейся на расстоянии 0,1 м от оси вращения, для момента времени t = 4 c.

Дано: = 10 + 20t - 2t²; r = 0,1 м; t = 4 c.

Найти: , , .

Решение. Полное ускорение точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального и нормального ускорений.

₍₁₎

Тангенциальное и нормальное ускорение точек вращающегося тела выражается формулами:

₍₂₎

₍₃₎

где - угловая скорость тела; - угловое ускорение тела; - расстояние точки от оси вращения.

Подставляя выражения (2), (3) в (1), находим

₍₄₎

Угловая скорость вращающегося тела равна первой производной от угла поворота по времени

В момент времени t = 4с угловая скорость

= (20 - 4•4) с^-1 = 4 с^-1.

Угловое ускорение вращающегося тела равно первой производной от угловой скорости по времени

Это выражение углового ускорения не содержит времени, следовательно, угловое ускорение имеет постоянное значение. Подставляя найденные значения и в формулу (26 ), получим

Направление полного ускорения определяется углами, которые вектор ускорения образует с касательной к траектории или с нормалью к ней

₍₅₎

₍₆₎

Найдем по формулам (2), и (3) значения и :

= - 4 • 0,1 = - 0,4 м/с²;

= 4² • 0,1 = 1,6 м/с².

Подставим эти значения в формулы (5), (6)

Пользуясь тригонометрическими таблицами, находим значения искомых углов

=76⁰; =14⁰.

Пример 10. Цилиндр весом 100 Н насажан на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря весом 20 Н. С каким ускорением будет опускаться гиря, весом 20 Н. С каким ускорением будет опускаться гиря, если ее предоставить самой себе (рис. 1).

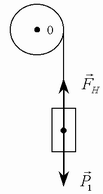
Рис. 1

Дано: Р = 100 Н; Р₁ = 20 Н.

Найти: а Решение. Линейное ускорение а гири равно тангенциальному ускорению точек цилиндра, лежащих на его поверхности, и связано с угловым ускорением вращения цилиндра соотношением

₍₁₎

где r – радиус цилиндра.

Угловое ускорение цилиндра определяется из основного уравнения динамики для вращательного движения

₍₂₎

где М – вращающий момент М, действующий на цилиндр; I – момент инерции цилиндра, который определяется по формуле

₍₃₎

Вращающий момент М, действующий на цилиндр, равен произведению силы натяжения шнура F_H на радиус цилиндра r.

₍₄₎

Сила натяжения шнура F_H находится из закона движения гири (второй закон Ньютона)

m₁a = P₁- F_H (5)

откуда

₍₆₎

С учетом (6) находим вращающий момент из (4) в виде

₍₇₎

Подставляя в формулу (2) полученные выражения для М и I определяем угловое ускорение

₍₈₎

Подставляя (8) в (1) и решая полученное уравнение относительно а, получаем

Проверяем единицу измерения

Пример 11. Через блок, выполненный в виде диска и имеющий массу 80 г. перекинута тонкая, гибкая нить, к концам которой подвешены грузы массами 100 и 200 г. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением пренебречь (рисунок 1).

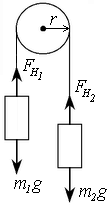
Рис. 1

Дано: m = 8·10^-2 кг; m₁ = 0,1 кг; m₂ = 0,2 кг.

Найти: а.

Решение. Применим к решению задачи закон сохранения энергии, согласно которому при отсутствии трения полная энергия изолированной системы тел остается неизменной во время движения этих тел; энергия при этом может только превращаться из потенциальной в кинетическую или наоборот. Напомним, что в механике полной энергией тела называется сумма его потенциальной и кинетической энергии.

Пусть в начальный момент движения потенциальная энергия первого груза увеличилась, а второго уменьшилась на h. Потенциальная энергия первого груза стала П₁ + m₁gh, второго П₂ + m₂gh. Кроме того, каждый груз, двигаясь с ускорением а, приобрел за это время скорость и кинетическую энергию, равную соответственно

и

Точно так же диск, вращаясь равноускоренно, приобрел угловую скорость и соответствующую ей кинетическую энергию I ²/2. Преобразуем выражение кинетической энергии диска. Так как

По закону сохранения энергии

После преобразования получим

Так как грузы двигались равноускоренно, то = 2 a h. Следовательно

откуда

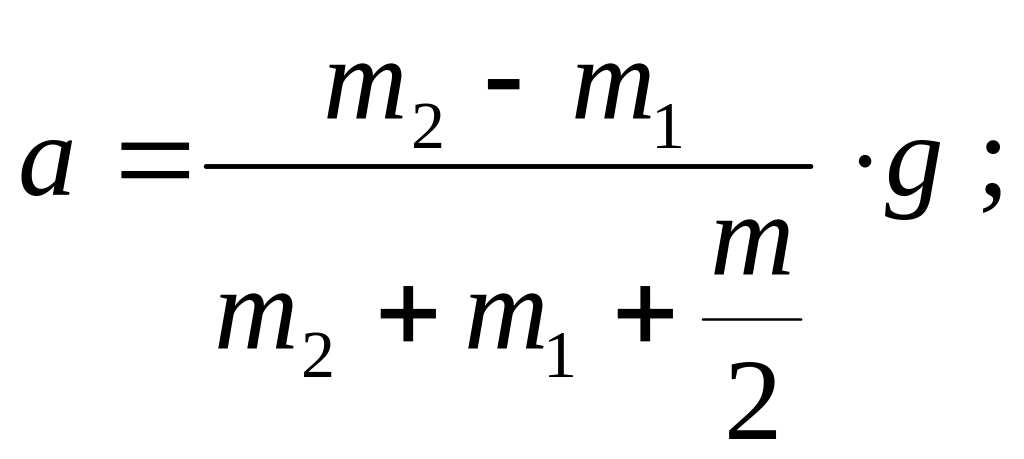
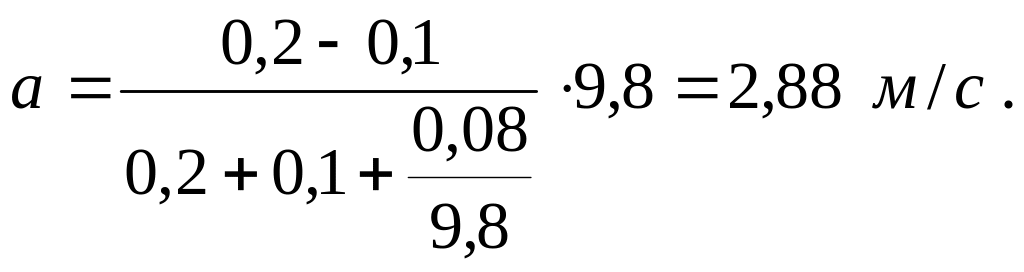
Пример 12. Дискообразный маховик массой 50 кг и радиусом 0,2 м вращается с частотой 480 об/мин. Будучи предоставленным самому себе, под влиянием сил трения маховик остановился. Найти момент сил трения, считая его постоянным, по следующим данным: 1) маховик остановился через 50 с; 2) маховик до полной остановки сделал 200 оборотов.

Дано: m = 50 кг; r = 0,2 м; n = 480 об/мин = 8 об/с; t = 50 c; N = 200.

Найти: М₁, М₂.

Решение. 1) Момент сил трения найдем из основного закона динамики для вращательного движения но = 0 (маховик остановился), поэтому откуда

(1)

Момент инерции диска определяется по формуле

(2)

Подставив выражение для момента инерции диска в формулу (1) и выразив угловую скорость через число оборотов в единицу времени , найдем

;

2) В условии дано число оборотов N, по которому можно найти угловое перемещение , а входит в формулу работы момента силы .

Работа, совершаемая маховиком, равна изменению его кинетической энергии, т.е.

(3)

так как = 0, то

(4)

откуда или с учетом выражения (2)

(5)

Знак “минус” показывает, что момент сил трения оказывает тормозящее действие.

Проверяем единицу измерения

Пример 13. Платформа в виде сплошного диска радиусом 1,5 м и массой 180 кг вращается по инерции около вертикальной оси с частотой 10 мин^-1. В центре платформы стоит человек массой 60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?

Дано: m₁ = 180 кг; R = 1,5 м; n = 10 мин^-1; m₂ = 60 кг.

Найти: .

Решение. Платформа вращается по инерции, следовательно, момент внешних сил относительно оси вращения z, совпадающий с геометрической осью платформы, равен нулю. При этом условии момент импульса L_z системы платформа-человек остается постоянным

(1)

где - момент инерции платформы с человеком относительно оси Z; - угловая скорость платформы.

Момент инерции системы I_z = I₁ + I₂ , где I₁ – момент инерции платформы; I₂ - момент инерции человека. С учетом этого равенство имеет вид

(2)

или

(3)

где значения величин со штрихами относятся к конечному состоянию системы.

Момент инерции платформы (сплошного диска) относительно оси Z при переходе человека не изменяется:

(4)

Момент инерции человека относительно той же оси будет изменяться. Если рассматривать человека как материальную точку, то в начальном положении (в центре платформы) момент инерции равен нулю. В конечном положении (на концу платформы) момент инерции человека

Подставим в формулу (3) найденные выражения моментов инерции, а так же выразим начальную угловую скорость вращения платформы с человеком через частоту вращения n ( ) и конечную угловую скорость - через линейную скорость человека относительно пола ( ):

После сокращения на и простых преобразований находим искомую скорость

Учитывая, что n = 10 мин^-1=1/6 с^-1, произведем расчет

Проведем единицу измерения определяемой величины

.

Пример 14. Какую скорость нужно сообщить ракете, чтобы она, стартовав с Земли, не вернулась на Землю? Сопротивление атмосферы не учитывать.

Дано: R₃ = 6,37·10⁶ м; g = 9,8 м/с²; R  .

Найти: .

Решение. По мере удаления ракеты от Земли потенциальная энергия ее увеличивается, а кинетическая – уменьшается. По закону сохранения энергии

(1)

где m – масса ракеты; М – масса Земли; G – гравитационная постоянная; и - скорости ракеты относительно Земли в начальный и рассматриваемый моменты.

После преобразования уравнения (1) имеем

Ракета не вернется на Землю, если ее скорость будет в бесконечности равна нулю, т.е. = 0 при R  . Следовательно

(2)

Из закона всемирного тяготения следует, что на поверхности Земли

(3)

где - ускорение свободного падения на поверхности Земли.

Подставляя (3) в (2), находим

Считая, что ракета приобретает нужную скорость , уже вблизи поверхности Земли, находим

Такая скорость необходима для преодоления гравитационного поля Земли (вторая космическая скорость).

Пример 15. Определить импульс и кинетическую энергию протона, движущегося со скоростью 0,7с (с– скорость света в вакууме).

Дано: = 0,7с.

Найти: р, W_K.

Решение. Импульс частицы – произведение массы на скорость:

(1)

Так как скорость близка к скорости света, то нужно учесть зависимость массы от скорости

(2)

где m – масса движущейся частицы, m₀ – 1,67·10^-27 кг – масса покоя протона,

с – 3·10⁸ м/с.

Заменив в формуле (1) массу m ее выражением (2), полу чим

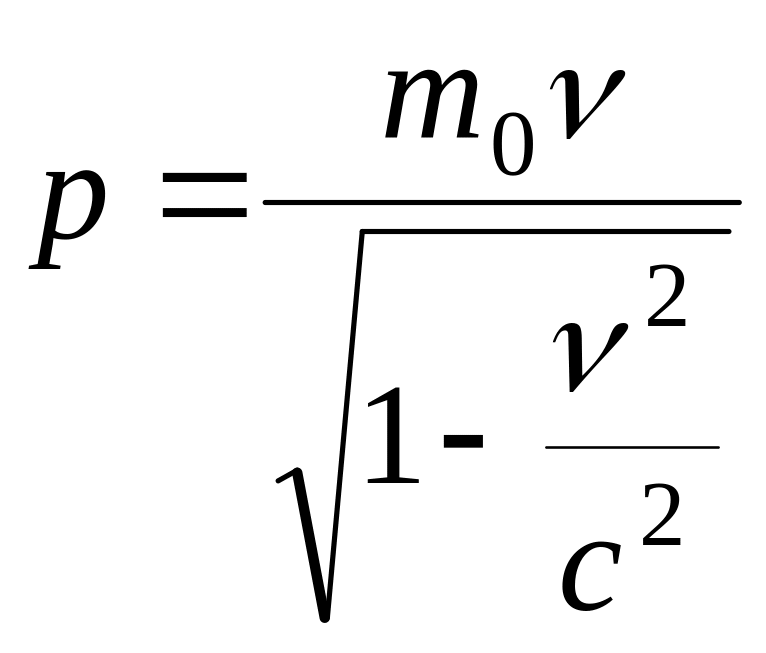(3)

Проведем вычисления

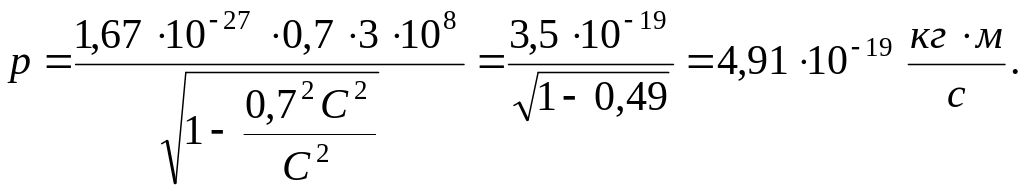
В релятивистской механике кинетическая энергия частицы W_K определяется как разность между полной энергией Е и энергией покоя Е₀, т.е. W_K = E – E₀. Так как

(4)

для W_K получаем следующее выражение

(5)