
- •Министерство образования и науки Украины Украинская инженерно-педагогическая академия
- •Общие положения
- •Общие указания к самостоятельной работе
- •Указания к решению задач и выполнению домашних заданий
- •1. Физические основы механики Основные формулы
- •Угол между полным и нормальным ускорениями:
- •Связь между полной энергией и импульсом релятивистской частицы
- •2. Примеры решения задач
- •Подставив (5) и (6) в уравнение (1), получим
- •Проверяем единицу измерения полученной величины
- •Найти: а Решение. Линейное ускорение а гири равно тангенциальному ускорению точек цилиндра, лежащих на его поверхности, и связано с угловым ускорением вращения цилиндра соотношением
- •3. Модульное задание 1 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Вариант 31
- •Вариант 32
- •Вариант 33
- •4. Модульное задание 2 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Вариант 31
- •Вариант 32
- •Вариант 33
- •5. Молекулярная физика и термодинамика Основные формулы
- •6. Примеры решения задач
- •Парциальное давление р1 и р2 выразим из уравнения состояния
- •7. Модульное задание 3 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Вариант 31
- •Вариант 32
- •Вариант 33
- •Приложения
- •Некоторые физические постоянные
- •Соотношения между единицами давления
- •Соотношения между единицами силы
- •Соотношение между единицами энергии и работы
- •Соотношение между единицами мощности
- •Литература
- •Оглавление
6. Примеры решения задач
Пример 1. В сосуде объемом 2 см3 находится смесь 4 кг гелия и 2 кг водорода при температуре 27 0С. Определить давление и молярную массу смеси газов.
Дано: V = 2 м3; m1 = 4 кг; m2 = 2 кг; 1 = 410-3 кг/моль; 2 = 2х
х10-3 кг/моль; Т = 300 К.
Найти: P, .
Решение. По закону Дальтона давление смеси газов равно сумме парциальных давлений газов, входящих в эту смесь: Р=Р1+Р2.
Парциальное давление р1 и р2 выразим из уравнения состояния
![]() ;
;
![]() ;
;
![]() ;
; ![]() ;
;
Давление смеси
![]() .
.
Молярная масса смеси
![]() ,
,
где 1 и 2 – число молей гелия и водорода.
Так
как
![]() и
и
![]() ,
для молярной массы смеси
,
для молярной массы смеси
 .
.
Подставляя численные значения, получим
![]()
 .
.
Ответ: Р = 2493 кПа; = 310-3 кг/моль.
Пример 2. Объем аргона, находящегося при давлении 80 кПа, увеличился от 1 до 2 л. На сколько изменится внутренняя энергия газа, если расширение производилось а) изобарно; б) адиабатно?
Дано: V1=1 л; V2=2 л; Р=0,8105 Па; =4010-3 кг/моль; i=3.
Найти: U.
Решение. а) Изобарный процесс. Изменение внутренней энергии при любом процессе определяется выражением
![]() .
.
Запишем уравнение Менделеева-Клапейрона для начального и конечного состояний газа:
![]() ;
;
![]() .
.
Вычитая из второго выражения первое, получим:
![]() .
.
Подставляя это выражение в формулу для U, получим
![]() .
.
Произведем вычисления:
![]() .
.
б) Адиабатный процесс. При адиабатном процессе теплообмен отсутствует, т.е. Q = 0 и работа совершается за счет внутренней энергии
А=-U .
Формула работы при адиабатном процессе имеет вид:
 ,
,
где
![]() .
При i
= 3
= 1,67.
.
При i
= 3
= 1,67.
Так
как
![]() ,
изменение внутренней энергии
,
изменение внутренней энергии
 .
.
Подставляя численные значения, получим:
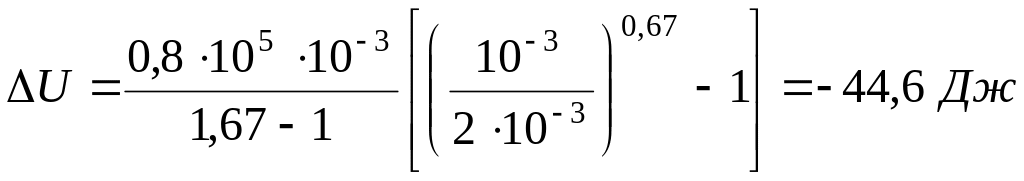 .
.
Знак минус означает что внутренняя энергия газа убывает.
Ответ: Uиз = 121 Дж, Uад = -44,6 Дж.
Пример 3. Тепловая машина работает по обратимому циклу Карно. Температура нагревателя Т1 = 500 К. Получая от нагревателя за цикл Q1 = = 1 кДж тепла, машина совершает работу А = 350 Дж. Найти КПД цикла, температуру охладителя и количество тепла, отдаваемое охладителю.
Дано: Т1 = 500 К, А = 350 Дж, Q1 = 1 кДж.
Найти: , Т2, Q2.
Решение.
КПД цикла
![]() .
Температуру охладителя Т2
найдем из выражения КПД цикла Карно
.
Температуру охладителя Т2
найдем из выражения КПД цикла Карно
![]() ,
,
отсюда
![]() .
.
Количество тепла, отданное охладителю, Q2=Q1 - A .
Подставляя численные значения, найдем искомые величины:
![]() .
.
Т2 = 500(1 - 0,35) = 325 К;
Q2 = (103 - 350) Дж = 650 Дж.
Ответ: =35 %, Т2 = 325 К, Q2 = 650 Дж.
Пример 4. Найти изменение энтропии при переходе 6 г водорода от объема 20 л под давлением 150 кПа к объему 60 л под давлением 100 кПа.
Дано: = 210-3 кг/моль, m = 60 г, Р1 = 150 кПа, V1 = 20 л, Р2 = 100 кПа, V2 = 60 л, i = 5.
Найти: S.
Решение. Запишем выражение для изменения энтропии S:
![]() . (1)
. (1)
Выразим
![]() Q
из первого начала термодинамики:
Q
из первого начала термодинамики:
![]() .
(2)
.
(2)
Температуру Т выразим из уравнения Менделеева-Клапейрона.
![]() ,
, ![]() . (3)
. (3)
Отсюда
![]() . (4)
. (4)
Подставим выражения (2), (3), (4) в выражение (1):
 . (5)
. (5)
Поскольку , изменение энтропии
![]() . (6)
. (6)
Подставляя численные значения, получим:
![]() .
.
Ответ: S = 71 Дж/К.
