2. Электрические цепи переменного тока Краткие теоретические сведения

Переменный ток, в противоположность постоянному току, периодически меняет свое направление. Кривая (функция) переменного тока или напряжения, соответственно, может иметь различную форму. На рис. 2.1 показаны некоторые из типичных для электротехники и электроники функций. Кроме того, различают однофазные и многофазные переменные напряжения и токи. Например, электроснабжение массовых потребителей осуществляется, как правило, посредством трехфазного тока.

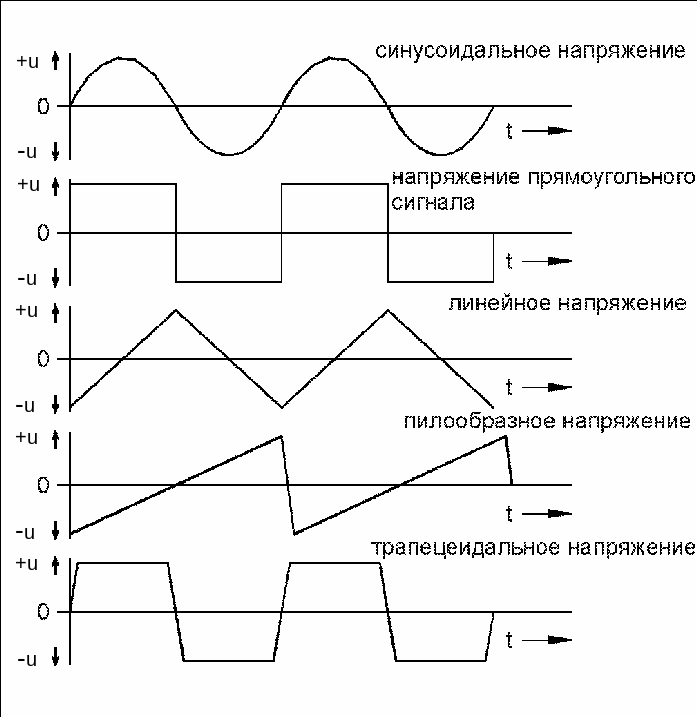
Рис. 2.1

Основные понятия синусоидального тока

На рис. 2.2 показаны напряжение и ток, как синусоидальные функции времени.

В течение одного периода T напряжение последовательно оказывается равным нулю, положительному максимуму (амплитудное значение) U_m, затем нулю, отрицательному максимуму и снова нулю.

Аналогично выглядит график изменения тока, но в общем случае он может быть сдвинут во времени относительно напряжения (отставать от напряжения или опережать его).

Величины e, u, i называют мгновенными значениями. Их наибольшие значения E_m, U_m, I_m называют амплитудными значениями. Величину называют угловой частотой. Аргумент синуса называют фазой, величины ψ_e, ψ_u, ψ_i – начальной фазой.

Рис. 2.2

Действующие и средние значения синусоидальных величин:

.

Мгновенные значения синусоидальных напряжения u и тока i выражаются так:

u = U_m  sin (t+_u),

i = I_m  sin (t+_i),

где _u и _i – начальные фазы напряжения и тока.

Разность фаз напряжения и тока (фазовый сдвиг):

 = _u - _i.

Другие параметры синусоидальных величин и формулы для их вычисления приведены ниже.

Частота f в Герцах (Гц) выражается как число периодов в секунду

f = 1  T.

Угловая частота  в рад  с равна

 = 2   f .

Действующие значения синусоидальных тока и напряжения равны

I = I_m / 2,

U = U_m / 2 .

Комплексный метод расчета

Изображение синусоидальной функции комплексным числом

В курсе теории линейных электрических цепей используются следующие формы записи комплексного числа:

алгебраическая ;

показательная ;

тригонометрическая ,

здесь – модуль комплексного числа;

– аргумент комплексного числа;

– действительная часть комплексного числа;

– мнимая часть комплексного числа.

Алгебраическая форма удобна при сложении и вычитании комплексных чисел, а показательная – при умножении, делении, возведении в степень, извлечении корня.

Комплексные значения токов и напряжений

Комплексные выражения синусоидальной функции времени, ее производной и интеграла приведены в табл. 2.1.

Таблица 2.1

Временная и комплексная записи	Функция	Производная функции	Интеграл от функции
Запись во временной области
Комплексная функция времени
Комплексная амплитуда
Комплексное действующее значение

Соответствующие комплексные амплитуды запишем так:

.

Согласно ГОСТу любое комплексное значение обозначается соответствующей буквой с чертой под ней, например , . Однако для величин, изменяющихся с течением времени синусоидально, разрешается комплексные величины обозначать с точкой над соответствующей буквой, таковы , напряжение , ток . Так что такие записи эквивалентны: , , .

Комплексные значения пассивных элементов электрической цепи

Пассивный элемент электрической цепи определяется своим комплексным сопротивлением – комплексным числом, равным отношению комплексного напряжения на зажимах данного элемента к комплексному току этого элемента:

.