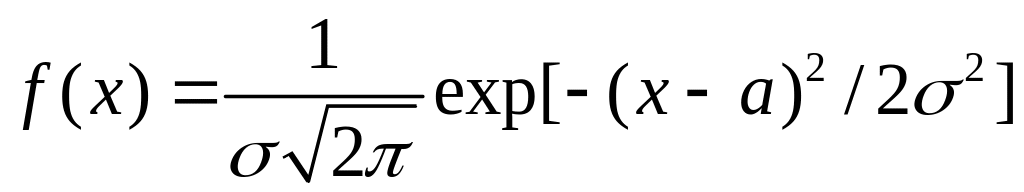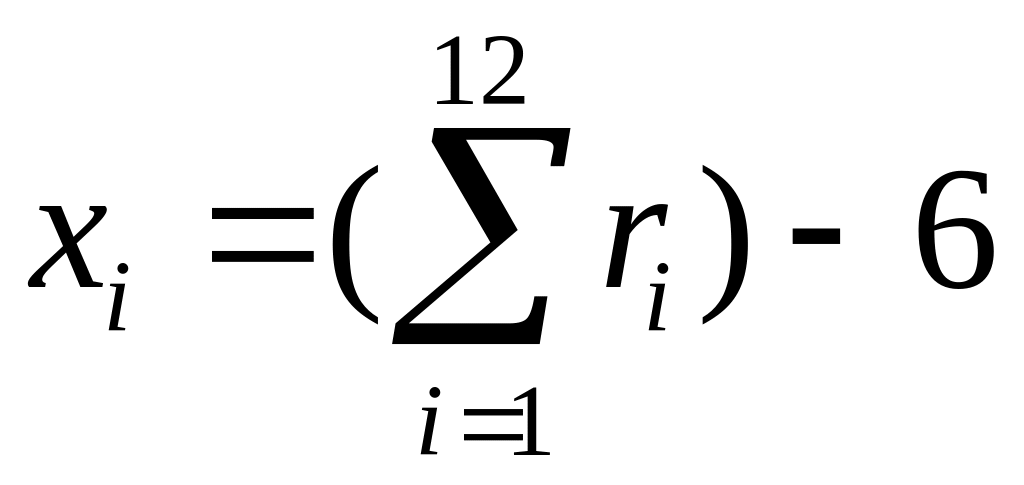1.3 Преобразование случайных величин [3,5]

Для статистической имитации необходимо уметь получать случайные числа с заданным законом распределения.

Любой закон распределения может быть получен из равномерного на интервале (01).

Получение (разыгрывание) дискретной случайной величины

Значения случайной величины и вероятности их реализации представим в виде таблицы:

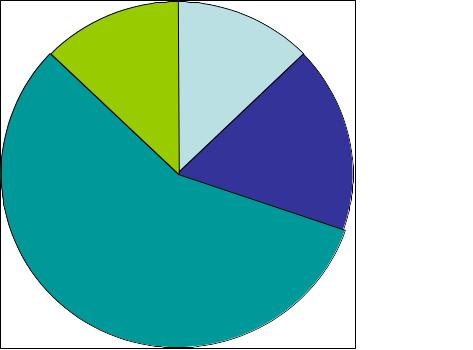
Соотношение (1.4) позволяет разбить интервал (0,1) на интервалов, так что длина каждого интервала равна вероятности реализации соответствующего значения .(рис.). Такое разбиение предоставляет следующий способ получения распределения дискретной случайной величины с помощью равномерного распределения на интервале (0,1).

Берётся случайное число из равномерного распределения на интервале (0,1) и определяется, в какой из интервалов это число попало. Если оно попало в интервал с номером , то случайной величине приписывается значение Затем берётся новое число из равномерного распределения, и вся процедура повторяется.

Рис.1.2 Рулетка, поделённая на секторы разного размера так, что размер сектора пропорционален вероятности дискретной случайной величины. Простой способ реализации распределения этой величины

Разыгрывание непрерывной случайной величины с произвольной плотностью распределения.

Существует несколько методов преобразования равномерного распределения на интервале (0,1) в распределение с заданной плотностью на интервале . Один из них состоит в решении следующего уравнения:

(1.11)

где число из равномерного распределения на (0,1), а значение случайной величины, распределённой с плотностью на .

Функция является монотонно возрастающей, так как . Любая прямая параллельная оси абсцисс пересекает функцию в единственной точке. Абсцисса этой точки является искомым значением случайной величины , распределённой с плотностью . Таким образом , уравнение имеет всегда единственное решение.

Выберем на оси абсцисс произвольный интервал внутри интервала . Точкам этого интервала соответствуют точки интервала на оси ординат . Поэтому если принадлежит интервалу , то принадлежит интервалу и наоборот. Значит,

(1.12)

Так как величина равномерно распределена на отрезке (0,1), то

(1.13)

Применение доказанного соотношения для плотности распределения в виде затухающей экспоненты.

Интегралы редко берутся. В этом главный недостаток рассмотренного метода. На практике часто достаточно использовать численное интегрирование. Плотность Распределение непрерывной величины часто достаточно рассматривать в конечном числе точек и плотность распределения представить в виде гистограммы. Значения интеграла удобно заранее вычислить для нужных точек и ввести в память в виде массива F. Тогда получение нового случайного числа с распределением по случайному числу из равномерного распределения сведётся просто к перебору элементов массива F.

Получение приближённого нормального распределения

В теории вероятностей и её приложениях большое значение имеет т.н. «нормальное распределение». Это непрерывное распределение с плотностью, записываемой в виде.

(1.14)

Оно характеризуется двумя параметрами и . Первый параметр равен математическому ожиданию и характеризует среднее арифметическое значение. Второй параметр равен квадратному корню из дисперсии и характеризует ширину распределения.

Нормальное распределение чрезвычайно часто встречается при статистическом анализе самых разных величин в науке и технике. Например, форма неоднородно уширенного спектрального контура, чаще всего, описывается нормальным распределением. Причину такой его распространённости даёт центральная предельная теорема теории вероятности, формулируемая следующим образом.

Если случайная величина представляет собой сумму большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму невелико, то имеет распределение близкое к нормальному.

Эта теорема даёт теоретическое обоснование для следующего метода получения нормально распределённых случайных чисел на основе стандартного генератора случайных чисел, дающего равномерно распределённые числа на промежутке (0,1).

Чтобы разыграть возможное значение нормальной случайной величины с параметрами и , надо сложить 12 случайных чисел из равномерного распределения на интервале (0,1) и из полученной суммы вычесть 6.

(1.15)

Число 12 в этом правиле возникло из-за того, что дисперсия для равномерного распределения равна 1/12. Дисперсия суммарного распределения равна сумме дисперсий. Чтобы дисперсия суммарного нормального распределения равнялась 1 необходимо складывать случайные числа 12ти равномерных распределений. Число 6 вычитается, чтобы центр нормального распределения был расположен на нуле. Точность получения нормального распределения может быть повышена за счёт увеличения числа слагаемых в сумме, но при этом, разумеется, значения и изменятся.

Основные положения главы 1

Необходимым элементом получения статистических моделей является генератор случайных чисел, который должен удовлетворять набору жёстких требований:

удовлетворять статистическим тестам;

иметь как можно более длинный период;

работать как можно более быстро;

воспроизводить одну последовательность чисел необходимое число раз.

Существует набор методов, которые, используя равномерное распределение случайных чисел на интервале (0,1), позволяют получить распределение случайных чисел с любой заданной плотностью распределения.