
- •Содержание
- •Глава 1 Случайные числа 7
- •Глава 2 Статистическое моделирование структуры материалов 18
- •Глава 3 Статистическое моделирование трансформации возбуждений в материалах фотоники 76
- •Введение
- •Глава 1 Случайные числа
- •1.1 Вероятность. Случайные величины с дискретным и непрерывным распределением
- •1.2 Получение и тестирование случайных чисел.
- •1.3 Преобразование случайных величин [3,5]
- •Глава 2 Статистическое моделирование структуры материалов
- •2.1 Основные представления о структуре стекла
- •2.2 Характеристики структуры. Статистические структурные модели
- •2.3 Релаксация структурных моделей методом Монте-Карло
- •2.4 Применение метода молекулярной динамики для моделирования структуры стекла и его физических параметров.
- •2.5 Неупорядоченная плотнейшая упаковка шаров.
- •2.6 Модель неупорядоченной сетки связей
- •2.7 Проблемы моделирования спектров лазерных материалов, активированных ионами рзэ.
- •2.8 Расчёты штарковской структуры спектров рзэ на основе кластерной стохастической модели.
- •2.9 Статистическое моделирование самоорганизации линейных дислокаций
- •Глава 3 Статистическое моделирование трансформации возбуждений в материалах фотоники
- •3.1 Процессы безызлучательной передачи возбуждений между оптическими центрами и их экспериментальные проявления
- •3.2 Микроскопическая модель передачи возбуждений для пары центров
- •3.2 Макроскопический подход. Метод балансных уравнений
- •3.4 Спектральная миграция. Моделирование на основе балансных уравнений.
- •3.5 Статистическое моделирование спектральной миграции методом Монте-Карло
- •3.6 Моделирование методом Монте-Карло ап-конверсионного тушения люминесценции эрбиевых лазерных стёкол.
- •3.7 Моделирование концентрационной деполяризации люминесценции
- •Заключение
- •Литература
- •Приложение
Приложение
Расчёт поля лигандов и штарковских расщеплений
Воздействие лигандов на состояния РЗ иона рассматривается в рамках теории возмущений для вырожденных уровней. При этом возмущение представляется в виде разложения по сферическим функциям, в котором в случае рассмотрения штарковских расщеплений достаточно ограничиться значениями n=2, 4, 6:
|
(П.1) |
Здесь
![]() – параметры поля лигандов; i,i
– угловые координаты 4f электрона; i –
номер 4f электрона,
– параметры поля лигандов; i,i
– угловые координаты 4f электрона; i –
номер 4f электрона,
![]() (i,i)
– сферические функции, связанные с
обычной формой
(i,i)
– сферические функции, связанные с
обычной формой
![]() соотношением:
соотношением:
|
(П 2) |
Параметры поля лигандов вычисляются по значениям координат атомов, составляющих ближайшее окружение РЗ иона.
Практические расчёты по вычислению матричных элементов возмущения сильно упрощаются при использовании метода «эквивалентных операторов» Стивенса [П 1, П 2]., в котором сферические функции заменяются их линейными комбинациями и выражение (П.1) переписывается в виде:
|
(П.3) |
Здесь
![]() – «эквивалентные операторы». Полные
таблицы матричных элементов этих
операторов, вычисленные для состояний
с определёнными значениями
– «эквивалентные операторы». Полные
таблицы матричных элементов этих
операторов, вычисленные для состояний
с определёнными значениями
![]() и
и
![]() ,
приведены в книгах [П.2].
,
приведены в книгах [П.2].
![]() вещественные
параметры кристаллического поля. Они
связаны простыми соотношениями с
параметрами
.
вещественные
параметры кристаллического поля. Они
связаны простыми соотношениями с
параметрами
.
![]() приведённые
матричные элементы (коэффициенты
Стивенса), в которых заключена специфика
рассматриваемого атомного состояния.
Для большинства уровней всех редкоземельных
ионов численные значения этих параметров
приведены в книге [П.2].
приведённые
матричные элементы (коэффициенты
Стивенса), в которых заключена специфика
рассматриваемого атомного состояния.
Для большинства уровней всех редкоземельных
ионов численные значения этих параметров
приведены в книге [П.2].
При
использовании выражения (П.3) для анализа
экспериментальных данных по штарковской
структуре кристаллов параметры
кристаллического поля
![]() ,
обычно, находятся путём подгонки расчёта
с экспериментом. Для симметричных
центров это удаётся сделать однозначно,
так как число штарковских энергий
существенно превышает число параметров
.
,
обычно, находятся путём подгонки расчёта
с экспериментом. Для симметричных
центров это удаётся сделать однозначно,
так как число штарковских энергий
существенно превышает число параметров
.
При моделировании параметры кристаллического поля (или ) приходится рассчитывать на основе микроскопической модели воздействия лигандов на состояния РЗ ионов. В случае если воздействие окружения на состояния РЗ ионов является исключительно кулоновским, явное выражение для параметров имеет следующий вид:
|
(П.4) |
Здесь
![]() – сферические координаты
– сферические координаты
![]() -го
иона матрицы:
-го
иона матрицы:
![]() заряд
-го
иона в единицах заряда электрона «
заряд
-го
иона в единицах заряда электрона «![]() »:
»:
![]() – среднее значение n-ой
степени радиуса 4f-электрона:
– среднее значение n-ой
степени радиуса 4f-электрона:
![]() – константа, введённая для учёта
экранировки электростатического поля,
действующего на 4f‑электроны;
– константа, введённая для учёта
экранировки электростатического поля,
действующего на 4f‑электроны;
![]() – числовые коэффициенты [П 2].
– числовые коэффициенты [П 2].
![]() – тессеральные
гармоники, которые связаны со сферическими
функциями
– тессеральные
гармоники, которые связаны со сферическими
функциями
![]() следующим образом:
следующим образом:
|
(П5) |
Параметры поля лигандов преобразуются при вращении системы координат как компоненты неприводимых тензоров второго, четвёртого и шестого рангов. Их усреднение по ансамблю неоднородных центров, где нельзя выбрать одинаковым образом локальные системы координат, не имеет смысла. Поэтому в качестве средних характеристик поля лигандов целесообразно использовать квадратичные инварианты соответствующих тензоров [П 3].
|
(П6) |
Для
расчётов параметров
,
инвариантов
![]() ,
штарковских расщеплений и спектров
последовательно рассматривались два
варианта модели поля лигандов: (а)
кулоновская модель и (б) суперпозиционная
модель, предполагающая, что воздействие
лигандов на РЗ ион сводится к перекрыванию
их оболочек с 4f оболочкой [П 4].
,
штарковских расщеплений и спектров
последовательно рассматривались два
варианта модели поля лигандов: (а)
кулоновская модель и (б) суперпозиционная
модель, предполагающая, что воздействие
лигандов на РЗ ион сводится к перекрыванию
их оболочек с 4f оболочкой [П 4].
Литература к приложению
П1 Альтшулер С.А., Козырев Б.М. Электронный парамагнитный резонанс. 2-е изд. – М: Наука,1972. – 672 с.
П2 Кустов Е.Ф., Бандуркин Г.А., Муравьёв Э.Н., Орловский В.П. п3. Электронные спектры соединений редкоземельных элементов, М.: Наука, 1984, 304 с.
П3 Пржевуский А.К., Инвариантные параметры и статистическое моделирование оптических центров РЗЭ в стёклах В сб. «Спектроскопия кристаллов» Л.: Наука, 1983, С. 82-95.
П4 Newman D.J. Theory of lanthanide crystal fields Advances in Pysics, 1971, v.20, p.197-256/

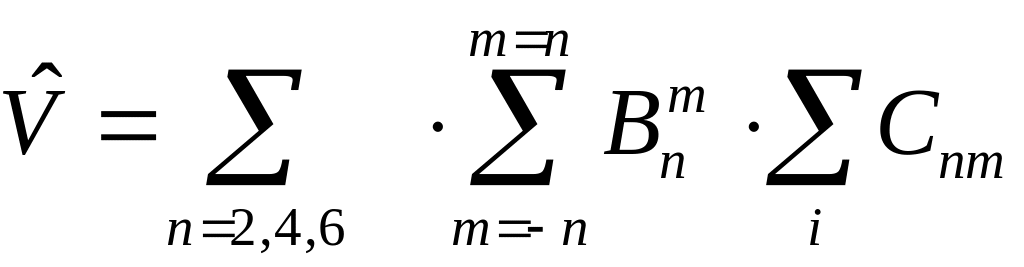 (i,i)
(i,i)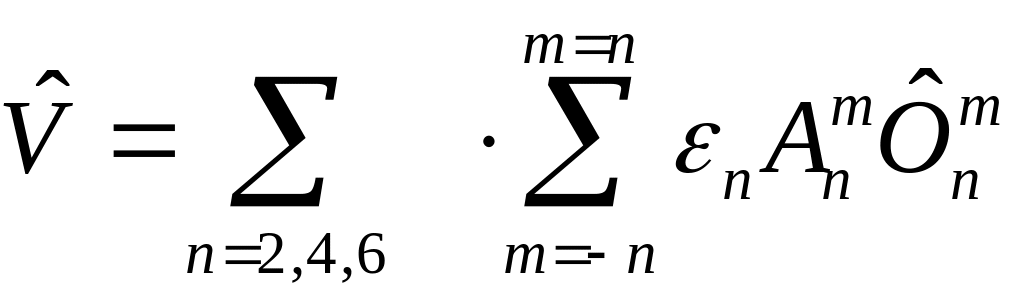 (i,i)
(i,i)
