
Контрольная работа / 2_433
.pdf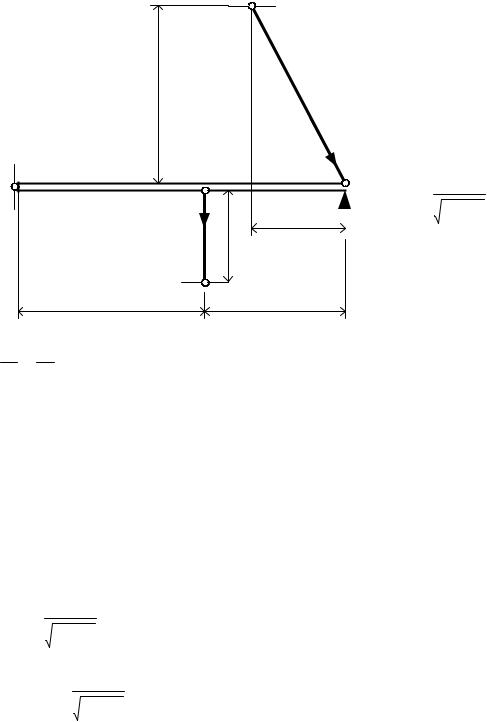
Задача №2
Абсолютно жесткий брус, опирающийся на шарнирно неподвижную опору, прикреплен к двум стержням с помощью шарниров.
1.Найти усилия и напряжения в стержнях, выразив их через силу F.
2.Найти допустимую нагрузку сравнением сравнением напряжений в двух стержнях с допустимым напряжением [ σ]=160МПа.
3.Найти граничную нагруженность системы и допустимую нагруженность, если граница текучести σт=260МПа, а запас прочности kт=1.5.
4.Сравнить рассчитанное значение Fдоп с граничной и допустимой нагруженностью.
a = 2.4 b = 1.8 c = 1.2 A = 1.4 10− 3
a
|
|
N1 |
c |
|
|
A |
|
|
|
|
|
|
|
a |
|
N1 |
÷ |
N2 = 1.143 То есть |
|
A |
|
2A |
|
Решение. SI MathCad ORIGIN = 1
1. Составляем уравнения равновесия совместно с
2A уравнением условия обеспечения жесткости системы
|
|
|
F = 1 N1 = 0 |
N2 = 0 |
||
|
N2 Given |
|
|
|
||
|
|
|
−a N − (a + b) a |
N + (a + b) F = 0 |
||
|
|
|
||||
|
|
|
||||
|
|
|
1 |
2 |
|
|
c |
|
F |
a2 + c2 |
|
|
|
|
|
|
|
|||
|
2c (a + b) N − a2 N |
|
|
|||
|
|
|
= 0 |
|||
|
|
|
||||
|
|
|
1 |
2 |
|
|
b |
|
|
N = Find(N1,N2) |
N = |
0.468 |
|
|
|
|
(в долях F) |
|||
|
|
|
|
|
|
0.819 |
σ1 >σ2
Допустимая нагрузка |
|
||
Fd = |
2A |
160 106 |
Fd = 9.572 × 105 |
|
N |
|
|
|
1 |
|
|
При достижении границы текучести в левом стержне
Ft = 2A 260 106 |
Ft = 1.037 |
× 10 |
6 |
|
|
||||
|
N1 1.5 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
Уравнение равновесия в граничном режиме |
|
|
|||||||
−a Ft − (a + b) a A 260 |
+ (a + b) Fd = 0 |
|
|
|
|||||
|
|
a2 + c2 |
1.5 |
|
|
|
|
|
|
|
|
a Ft + (a + b) a A |
260 |
|
|
|
|
|
|
Fd = |
|
a2 |
+ c2 |
1.5 |
|
|
Fd = 5.926 |
× 10 |
5 |
|
a |
+ b |
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
Полученное значение почти вдвое меньше рассчитанного по допустимой нагрузке
