
Контрольная работа / 9_433
.pdf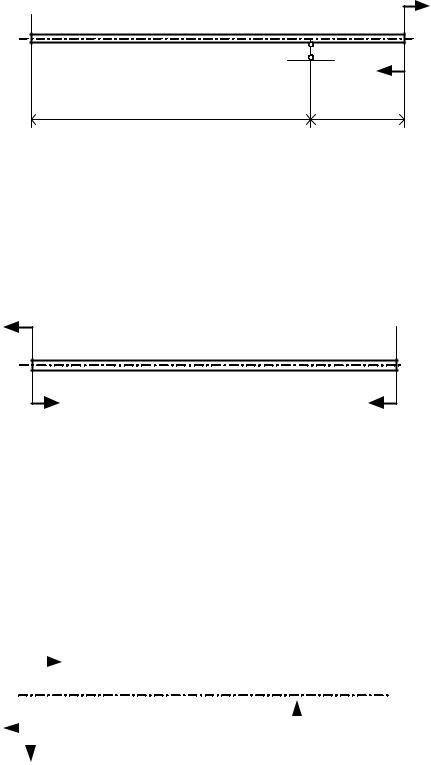
Задача №9
Для статически неопределимой балки постоянного поперечного сечения
1.Построить эпюры изгибающих моментов и поперечных сил.
2.Подобрать балку двутаврового сечения при [ σ]=160 МПа.
3.Изобразить вид упругой линии.
M
3l/4 |
l/4 |
l = 3.8 |
M = 40000 |
SI MathCad |
Решение.
Количество независимых уравнений равновесия - 2, количество неизвестных реакций -3. Степень неопределенности 3-2=1
В качестве основной системы выберем защемленную балку, отбросив опору. Для ее расчета составим уравнения равновесия и определим реакции опор.
MA M 
RA = 0 MA = M
Прогиб в точке B от действия внешних сил
|
3 |
2 |
|
|
|
|
|
M A |
|
l |
|
9Ml |
2 |
|
|
|
||||
EIy = |
4 |
|
= |
|
||
2 |
|
32 |
|
|||
|
|
|
|
|||
Расчетная схема для определения прогиба от лишней силы
MA
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
RA |
|
|
|
|
|
|
|
|
RB |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
M A |
= |
|
3 |
lRB |
|
3 |
2 |
3 |
3 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
4 |
|
|
M A |
|
l |
RA |
|
|
l |
9 |
|
|
||||
|
|
|
|
|
|
|
4 |
|
|
||||||||||||
R |
|
|
= R |
EIy = − |
4 |
|
+ |
|
|
= − |
R l3 |
||||||||||
|
|
2 |
|
|
6 |
|
64 |
||||||||||||||
|
A |
|
|
|
|
B |
|
|
|
|
|
|
|
B |
|||||||
Приравняв сумму прогибов от внешних сил и лишней реакции, получим
RB = |
2M |
RB = 21052.632 |
||
l |
|
|||
|
|
|||
Составляем уравнения равновесия с учетом полученной реакции
Given
−RA + RB = 0
−MA − M + 34 l RB = 0
Решение этой системы
RA
= Find(RA,MA) RA = 21052.632 MA = 20000
MA
Изгибающие моменты и поперечные силы по участкам |
|
|
|
|||||||||
M(x) = |
|
−MA + RA x |
|
|
3 l |
|
|
Q(x) = |
|
RA |
|
|
|
|
|
|
|
|
|||||||
|
|
−MA + RA x − RB |
x − |
if x > |
3l |
|
RA − RB if x > |
3l |
||||
|
|
|
|
|
|
|
|
|
||||
|
4 |
4 |
|
4 |
||||||||
|
|
|
|
|
|
|
|
|||||
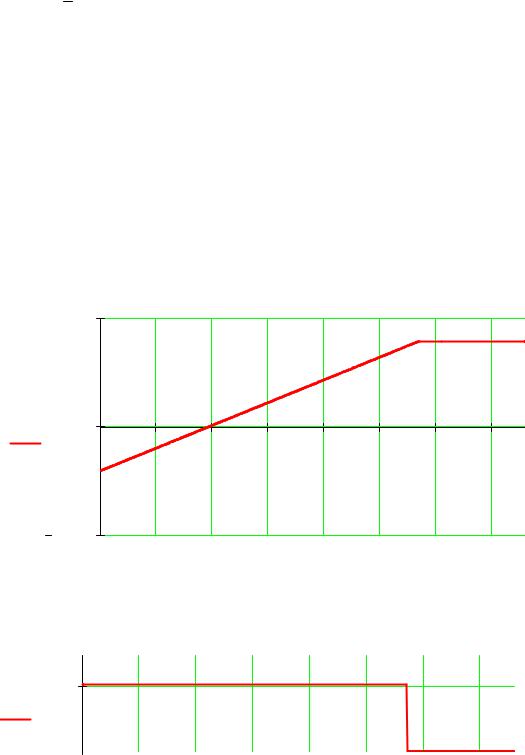
Строим эпюры
5 .104
M(x) |
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
|
5 .104
x
2 .104
Q(x)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
|||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
Максимальный момент |
|
|||
Mm = M(l) |
Mm = 40000 |
M = 40000 |
||
Момент сопротивления |
|
|||
W = |
Mm |
|
W = 2.5 × 10− 4 |
|
160 106 |
|
|||
|
|
|
||
По таблицам сортамента (ГОСТ8509-72) подбираем двутавр №20b
W = 250 см3
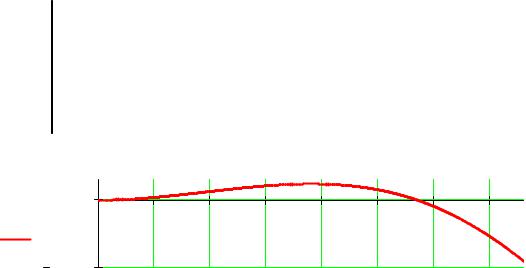
Уравнение упругой линии
EIy(x) = |
MA x2 |
− |
RA x3 |
|
2 |
|
6 |
||
|
|
|
||
|
|
|
|
|
|
|
3 |
|
3 |
|
|
MA x2 |
|
RA x3 |
|
RB |
x − |
|
l |
|
|
3 l |
|
− |
+ |
4 |
|
if x > |
|||||||
2 |
|
6 |
|
6 |
|
|
|
4 |
|||
|
|
|
|
|
|
|
|
||||
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
EIy(x)
5 .104
x
