Таблица 18

Вариант	T	mN	σN	Вариант	T	mN	σN
1	200	0	1	14	250	0	1.8
2	200	0	1.5	15	250	0	2.8
3	200	0	2	16	250	0	3.8
4	200	0	2.5	17	250	0	0.8
5	200	0	3	18	250	0	2.2
6	200	0	3.5	19	250	0	1.2
7	300	0	1	20	400	0	3.2
8	300	0	1.5	21	400	0	1.5
9	300	0	2	22	400	0	2
10	300	0	2.5	23	400	1	2.5
11	300	0	3	24	400	1	3
12	300	0	1.7	25	400	1	1.0
13	300	0	2.7	26	400	1	2.0

Лабораторная работа № 11 динамические модели объектов управления

Цель работы: изучение методов получения и исследования динамических характеристик объектов управления с использованием инструментальных средств Mathcad.

Порядок выполнения работы

Изучить математическую модель смешения двух компонентов и построить для линеаризованной системы дифференциальных уравнений графическое отображение динамики процесса для измеряемых и не измеряемых выходов.

Решения найти при нулевых начальных условиях и различных входных воздействиях:

• аналитическим способом;

• одним из численных методов, реализованным в виде процедуры Mathcad.

Теоретические сведения

Среди методов получения математических моделей объектов управления наиболее распространенными являются:

• экспериментальные или активные [10, 12], заключающиеся в подаче на входы объекта воздействий определенной формы (ступенчатых, импульсных, гармонических) и анализе полученных откликов;

• пассивные, основанные на использовании результатов опытной эксплуатации;

• аналитические;

• комбинированные.

Экспериментальное исследование динамики объектов с целью получения переходных процессов (кривых разгона) или частотных характеристик связано с существенными материальными затратами и не всегда возможно в необходимых интервалах изменения входных воздействий. Последний недостаток присущ также и пассивному методу. Более широкими возможностями обладает метод аналитического описания, но в большинстве случаев проблема его получения для технологических объектов достаточно сложная, так как движение материальных потоков описывается системой нелинейных дифференциальных уравнений в частных производных, уравнения материальных и тепловых балансов, фазовых переходов также нелинейные, физические величины, используемые в описании процессов тепло- и массообмена зависят от многих факторов и не всегда известны на стадии разработки системы управления. Их уточнение возможно в процессе эксплуатации объекта или предварительного его активного исследования (комбинированный метод).

Рассмотрим задачу аналитического получения математического описания объекта на примере смесителя двух компонентов. На рис. 60 представлена схема смешения. Емкость, в которой происходит непрерывное перемешивание поступающих потоков жидкостей имеет объем V. Первый поток имеет расход и концентрацию . Второй поток имеет расход и концентрацию . После смешения на выходе из емкости общий расход жидкости составляет , а концентрация вещества – , – уровень жидкости.

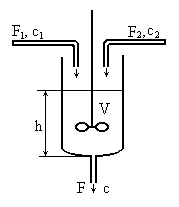
Рис. 60. Схема смешения

Составим уравне­ния баланса масс, которые имеют вид:

(59)

где [м³/с] – потоки, которые поступают в бак с концентрациями [кмоль/с] соответственно, а выходной поток имеет расход [м³/с] и концентрацию  [кмоль/с]. Расход выходного потока зависит от высоты столба жидкости [м] в соответствии с законом истечения:

, (60)

где [м²/с] – экспериментальная константа; [м²] – площадь поперечного сечения бака.

Подставляя это выражение в (59) получаем нелинейную модель смешения:

В установившемся состоянии, полагая в (59) производные равными нулю, получаем:

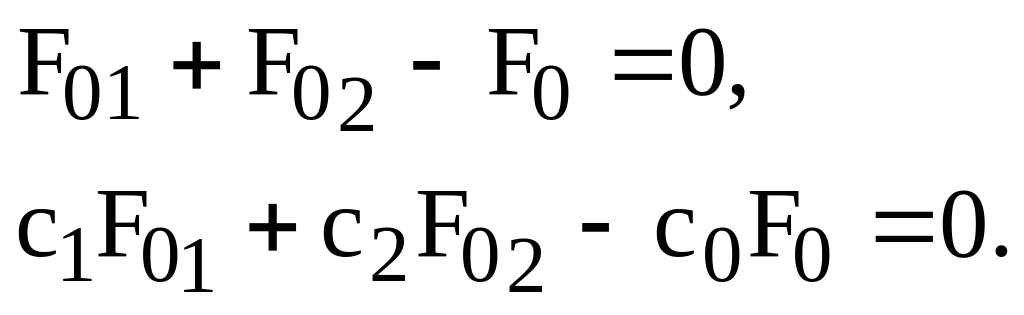(61)

Аналогично вместо (60) в установившемся состоянии будем иметь:

. (62)

При заданных эти уравнения можно разрешить относительно .

Предположим, что возникли небольшие отклонения относительно установившегося состояния. Тогда можно записать:

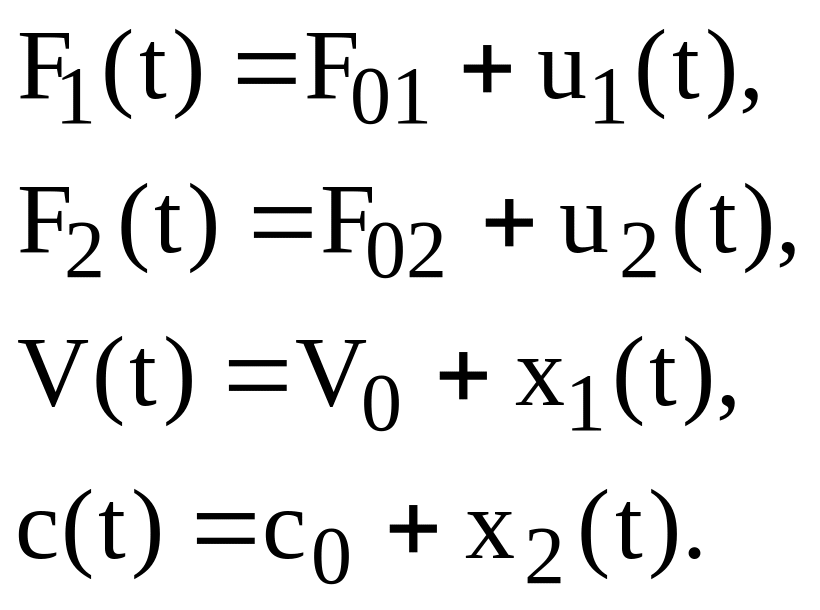(63)

Здесь u₁(t), u₂(t) [м³/с] естественно рассматривать как входные переменные относительно отклонений, а х₁(t) [м³], х₂(t) [кмоль/с] соответственно как переменные состояния.

Задача состоит в исследовании динамики процесса смешения и его поведения при использовании различных законов регулирования. В дальнейшем рассматривается процесс при небольших отклонениях от установившегося состояния. Учитывая что величина потока F(t) имеет нелинейную зависимость, определенную выражением (60), целесообразно провести линеаризацию. Из (60) и (62) имеем, с учетом третьего соотношения в (63):

(64)

где [с] – постоянная времени объекта.

Подставляя (63) и (64) в уравнения баланса (58), получаем линеаризованную систему уравнений в виде

, (65)

. (66)

Исключая из (66) с помощью (65), полученную систему уравнений можно представить в матричном виде

.

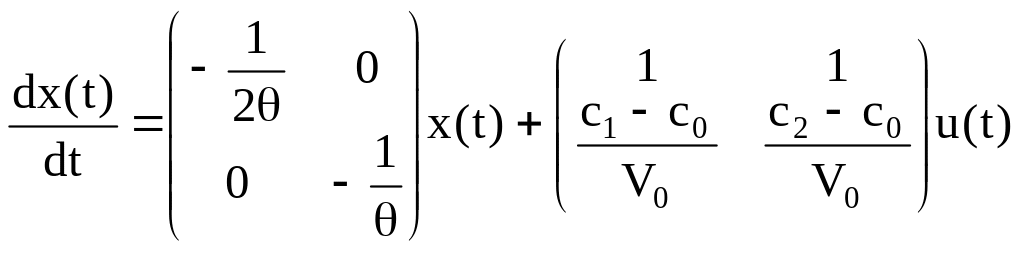Здесь x(t)=( а . Для более полного описания введем выходные переменные, которые непосредственно доступны для измерения.

В данном случае положим

,

.

В матричном виде это выражение можно записать:

В результате получаем линеаризованную математическую модель смешения, которую можно записать в виде:

, (67)

(68)

Здесь матрицы А, В и С определены следующими выражениями:

, , .

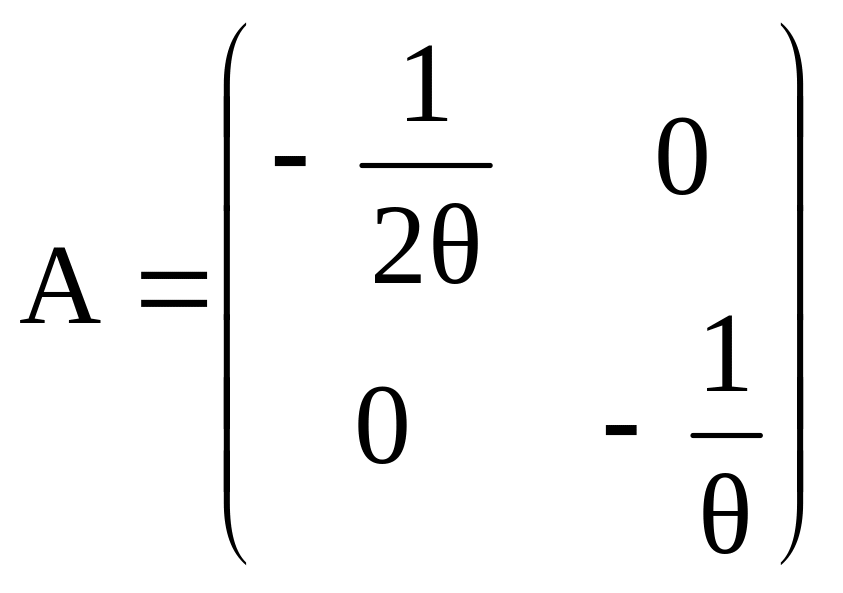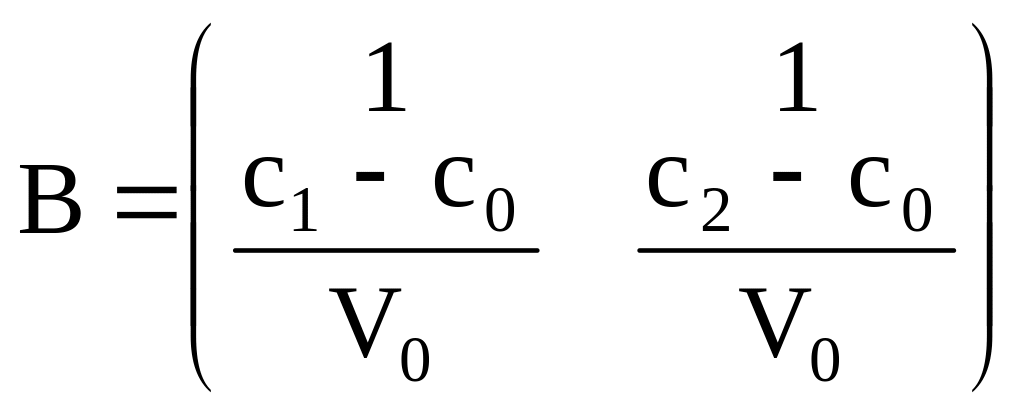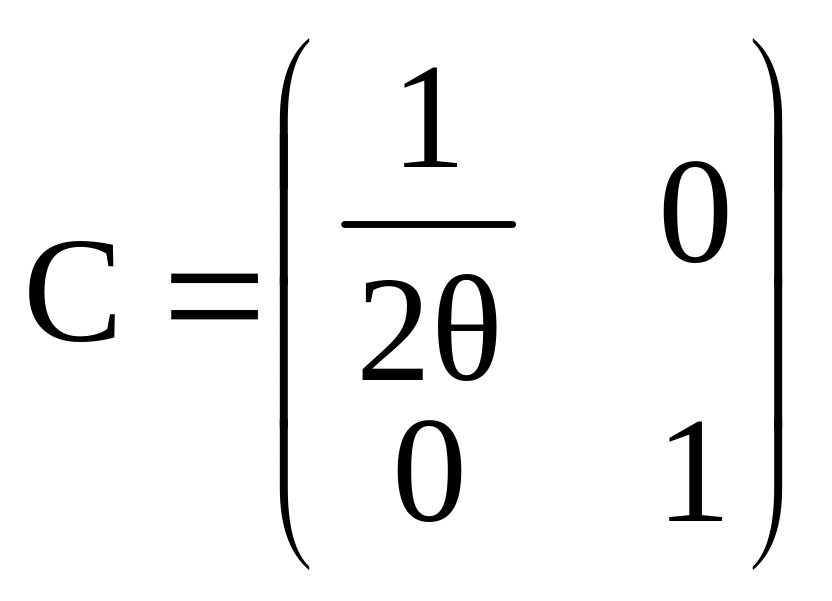Решение линейного дифференциального уравнения (67) подставляем в (68) и в результате получаем выражение относительно выходной переменной , которое описывает динамическую связь между измеряемым входом и выходом системы.