Курсовая работа [вариан 8] / Индивидуальные задачи
.doc
Индивидуальные задачи
Индивидуальная задача №1
Проверить прочность и жесткость стержневой системы, если вертикальное перемещение узла В не должно превышать величины [] = 3 мм.
Дано: F = 100 кН, [1] = 160 МПа, А1 = 5 см2, l1 = 1 м,
Е1 = 200 ГПа, [2] = 150 МПа, А2 = 6 см2, l2 = 2 м,
Е2
= 100 ГПа.
-
Вычисление значений реакций стержней
-
Расчёт на прочность.
-
Расчёт на жёсткость
Ответ:
Индивидуальная задача №2
Ч
угунный
круглый стержень вставлен в стальной
цилиндр, причем длина стержня больше
длины трубки на
= 0,05 мм, а площади их сечений одинаковы,
т.е. Ас
= Ач
= А.
Подобрать площади сечений с таким
расчетом, чтобы после приложения силы
F
= 300 кН в стержне и трубке возникли
напряжения одинаковой величины, если
Ес = 200 ГПа, Еч = 120 ГПа, l = 40 см.
Уравнение статики:
Уравнение деформации:
Ответ: 40см2 .
Индивидуальная задача №3
Брус прямоугольного сечения ab = 85 см, склеенный по наклонному сечению, сжат силой F = 12 кН. Предел прочности клеевого соединения на срез ср = 1,5МПа. При каких значениях угла обеспечивается не менее чем двукратный запас прочности соединения?
Решение.
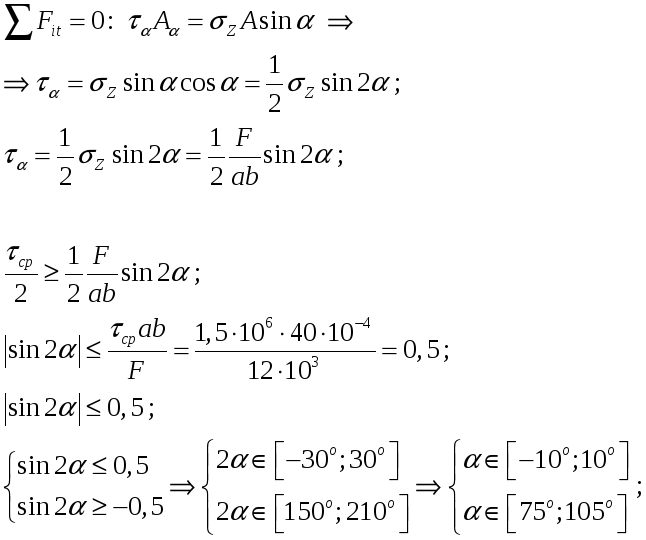
Ответ:
или
.
Индивидуальная задача №4
Вал диаметром 90 мм передает 90 л.с. Определить предельное число оборотов вала, если допускаемое касательное напряжение равно 60 МПа.
Дано: d=90мм,
P=90 л.с. =66,240 КВт,
[τ] = 60 МПа;
Решение:
Запишем условие прочности вала:
Т.к.
момент в каждом сечении вала одинаков
то
.
Ответ: Не менее 75 об/мин.
Индивидуальная задача №5
Сравнить допускаемые нагрузки для двух вариантов расположения поперечного сечения чугунной балки, если [с] = 4[р].
Ответ: [F2] / [F1] = 1,25.
Решение:
1 вариант
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 вариант
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: [F2] / [F1] = 1,25.
Индивидуальная задача №6
Какую силу F можно приложить в дополнение к погонной нагрузке q = 6 кН/м, чтобы наибольшие нормальные напряжения не превышали 160 МПа, а наибольший прогиб не превосходил 1/250 пролета балки l = 2 м.
Ответ: F = Fж = 16,26 кН.
Дано: [] = 160 МПа, l = 2 м, Е1 = 200 ГПа, [f] = 0,008м.
Решение:
1) Из условия прочности имеем
max = Mmax / Wx [].
Отсюда, учитывая
что
и для двутавра №24 Wx=289см3,
находим допустимую величину силы F:
.
2) Далее, согласно условию жесткости
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
,
Определим перемещение точки B.
C учетом того, что для двутавра №24 Ix=3460см4 находим допустимую величину силы F:
Из двух полученных значений принимаем меньшее, т.е.
F = min{Fпч, Fж} = Fж = 16,26 кН.
Ответ: F = Fж = 16,26 кН.