ЗМодуль 2. Пряма та площина. Рівняння прямої на координатній площині. Основні задачі геометрії прямих на координатній площині.

1. Знайти віддаль між прямими і .

2. Скласти рівняння бісектриси внутрішнього кута A трикутника , якщо .

3. Скласти рівняння прямої, нахилом до осі Ох під кутом 150⁰, яка відтинає на осі Оу відрізок, рівний - . Знайти точку перетину прямої з віссю абсцис.

(Відповідь: х + 3у+1=0, ( - ;0) ).

4. Дано трикутник АВС: А(-2,3), В(4;1), С(6,-5). Написати рівняння медіани цього трикутника, проведеної із вершини А. Система координат афінна

(Відповідь: 5х+7у-11=0).

5. Написати рівняння прямої, що паралельна до прямої 2х+5у=0 і утворює разом з осями координат трикутник, площа якого дорівнює 5.

(Відповідь: 2х+5у 10=0).

6. Скласти параметричне рівняння прямої, що походить через А(-6;-4) і має кутовий коефіцієнт 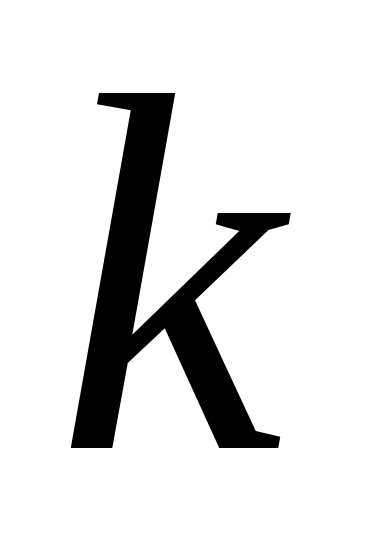=- . С.к.а.

(Відповідь: х=-6+7t, y=-4-3t).

7. Через М(2;5) провести пряму, рівновіддалену від точок Р(-1;2) і Q(5;4). С.к.а.

(Відповідь: х-2=0, х-3у+13=0).

8. Знаючи рівняння двох сторін паралелограма х-3у=0 і 2х+5у+6=0 та одну із його вершин С(4;-1) скласти рівняння двох інших сторін паралелограма. С.к.а.

(Відповідь: х-3у-7=0, 2х+5у-3=0).

9. В трикутнику АВС відомі; сторона АВ: 4х+у-12=0, висота ВН: 5х-4у-15=0 і висота АН:2х+2у-9=0. Написати рівняння двох інших сторін і третьої висоти.

(Відповідь: (ВС):х-у-3=0; (АС)4х+5у-20=0; (СН):3х-12у-1=0).

10. Через початок координат провести прямі, що утворюють з прямою 5х-6у+2=0 кути, тангенси яких рівні .

(Відповідь: 72х-у=0: 12х+71у=0).

11. Дано дві точки А(3;3), В(0;2). На прямій х+у-4=0 знайти точку із якої відрізок АВ видно під кутом 45⁰ .

(Відповідь: М₁(4;0), М₂(-1;5) ).

12. Через точку перетину прямих 3х-5у+2=0, 5х-2у+4=0 провести пряму, паралельну прямій 2х-у+4=0. С.к.а.

(Відповідь: 38х-19у+30=0.)

13. Через точку перетину прямих 3х-у=0, х+4у-2=0 провести пряму, перпендикулярну до прямої 2х+7у=0.

(Відповідь: 91х-26у-2=0).

14. Визначити відстань від точок (1;0) і (-1,2) до прямої 3х-у+4=0

(Відповідь: , ).

15. На прямій х-3у+13=0 знайти точки, що відстоять від прямої х+2у+3=0 на відстані .

(Відповідь: (-10;1), (-4;3) ).

16. Скласти рівняння бісектриси того кута між прямими х+у-3=0, 7х-у+4=0, в якому лежить точка (-1;5).

(Відповідь: 12х+4у-11=0).

17. На прямій 7х+3у-14=0 знайти точки, сума відстаней кожної із яких до двох точок (2;3) і (-1;4) рівна 8.

(Відповідь: (2;0)і (-1;7) ).

18. Скласти рівняння сторін трикутника , знаючи одну із його вершин

А(3;-4) і рівняння двох висот: 7х-2у-1=0, 2х-7у-6=0.

(Відповідь: 2х+7у+22=0, 7х+2у-13=0, x-y+2=0).

19. Написати рівняння прямої, що проходить через точку перетину прямих: 7х-у+3=0 і 3х+5у-4=0, і через точку А(2;-1). С.к.а.

(Відповідь: 25х+29у-21=0).

20. Дано дві вершини трикутника А (-6;2), В(2;-2), і точка Н(1;2) перетину його висот. Знайти координати вершини С.

(Відповідь: С (2;4) ).

21. Через точку (3;1) провести прямі, що нахилені до прямої 2х+3у-1=0 під кутом 45⁰.

(Відповідь: 5х+у-16=0, х-5у+2=0).