
- •Вектори. Лінійні операції над векторами. Лінійна залежність векторів.
- •Скалярне, векторне та мішане множення векторів.
- •ЗМодуль 2. Пряма та площина. Рівняння прямої на координатній площині. Основні задачі геометрії прямих на координатній площині.
- •Площина і пряма у координатному просторі, найпростіші задачі.
- •ЗМодуль 3. Лінії другого порядку. Канонічні рівняння ліній другого порядку, основні геометричні властивості цих ліній.
- •ЗМодуль 4. Лінії другого порядку, задані загальними рівняннями
- •ЗМодуль 5. Канонічні рівняння поверхонь другого порядку.
- •ЗМодуль 6. Загальні рівняння поверхонь другого порядку.
Умови задач, рекомендованих для індивідуального розв’язання з курсу «Аналітична геометрія».
ЗМодуль 1. Системи координат. Векторна алгебра.
Декартові системи координат на прямій,
на площині та у просторі. Основні задачі координатної геометрії.
Знайти координати x і y центра ваги трикутника АВС з вершинами
 ,
,
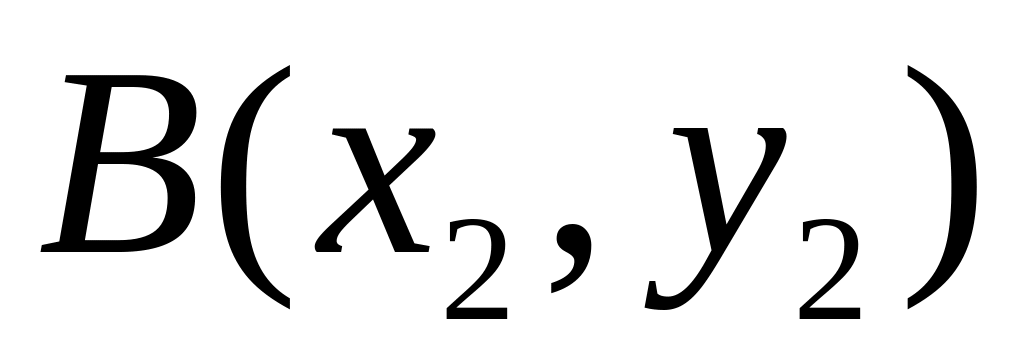 та
та
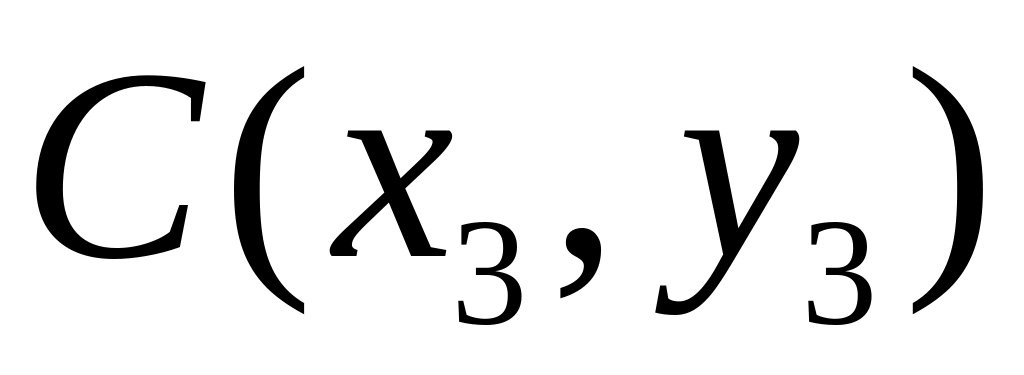 .
.
(Відповідь:
![]() ),
),
![]() .)
.)
Знайти в площині
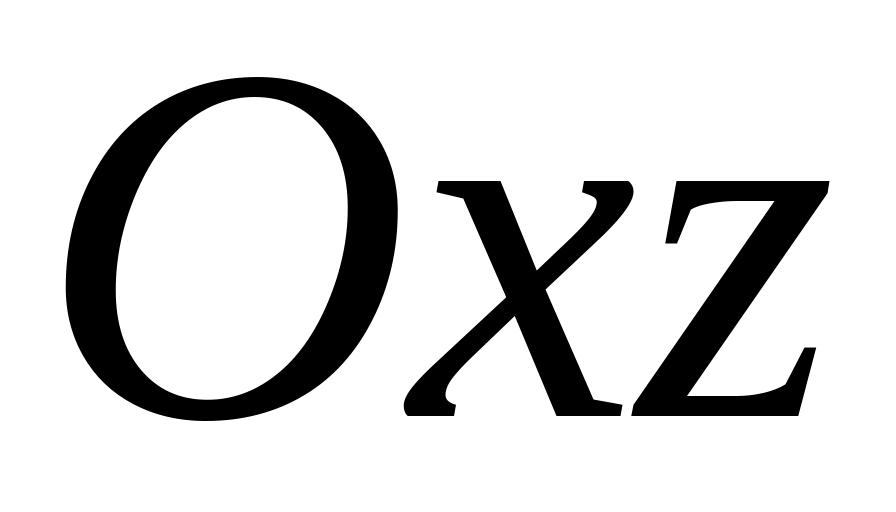 точку рівновіддалену від трьох точок
точку рівновіддалену від трьох точок
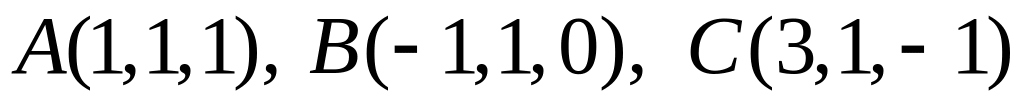 .
(Відповідь:
.
(Відповідь:
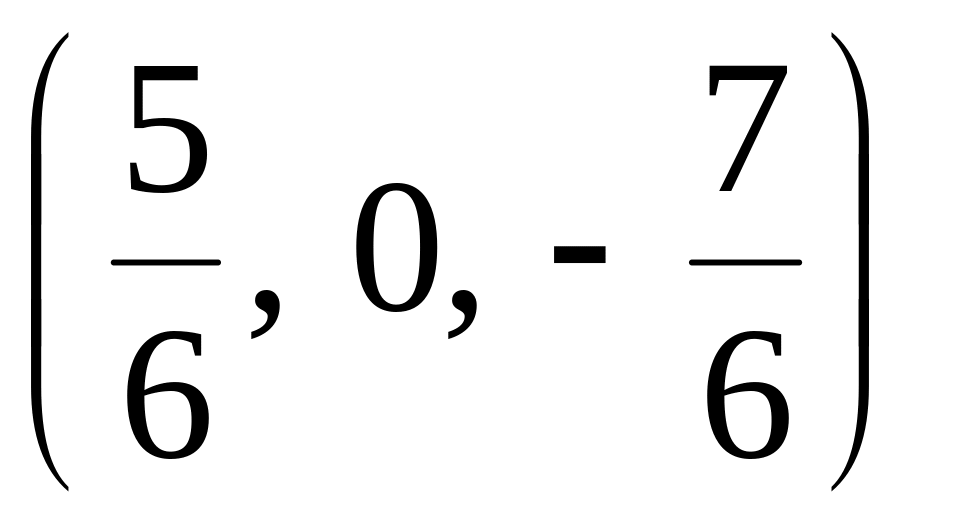 )
)Дві вершини трикутника знаходяться в точках (5, 1) і (–2, 2); третя вершина лежить на осі
 .
Знайти координати третьої вершини,
знаючи, що площа трикутника дорівнює
10.
.
Знайти координати третьої вершини,
знаючи, що площа трикутника дорівнює
10.
(Відповідь: (32, 0) і (–8, 0))
Обчислити площу трикутника, вершини якого А(r1, φ1), В(r2, φ2),
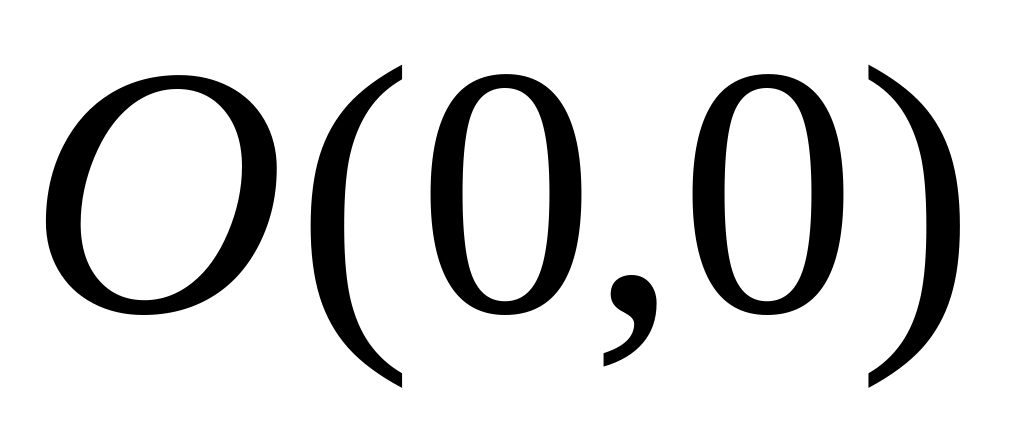 задано полярними координатами (φ1>φ2).
задано полярними координатами (φ1>φ2).
(Відповідь:
![]() )
)
Дано дві суміжні вершини паралелограма
 А(-1;3),
В( 2;-1 ). Знайти дві інші вершини при
умові, що діагоналі паралелограма
паралельні осям координат. (Відповідь:
С( 5,3 ), D( 2,7 ) або С(-1;-5), D (-4;-1))
А(-1;3),
В( 2;-1 ). Знайти дві інші вершини при
умові, що діагоналі паралелограма
паралельні осям координат. (Відповідь:
С( 5,3 ), D( 2,7 ) або С(-1;-5), D (-4;-1))
На осях координат знайти точки, кожна з яких рівновіддалена від точок (1,1) та ( 3;7 ). (Відповідь: (14,0) і (0;
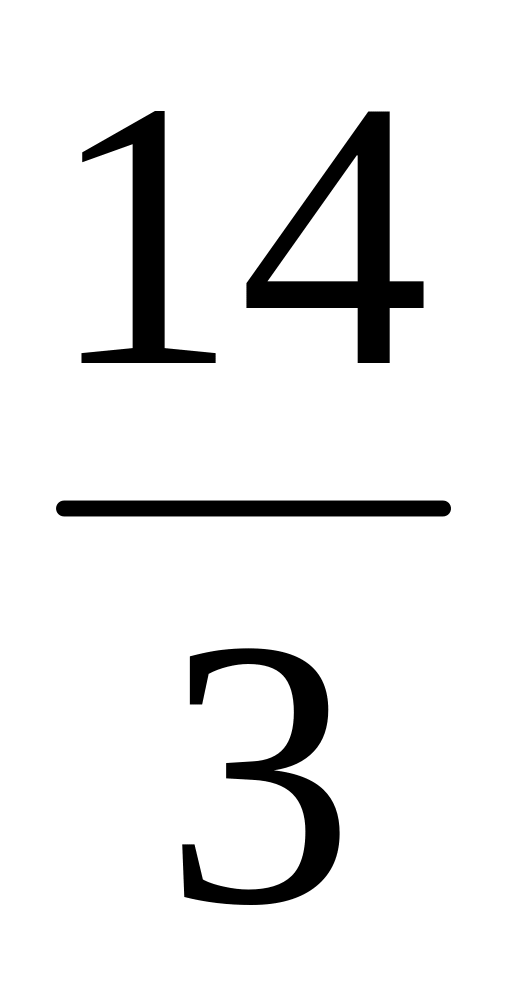 )
)
)
)Знаючи дві протилежні вершини ромба А( 8;-3 ) і С ( 10,11 ), знайти дві інші його вершини при умові, що довжина сторони ромба дорівнює 10. ( Відповідь: В(2;5), D(16;3) ).
Дано три послідовні вершини трапеції А(-2;-3 ), В(1,4), С(3,1). Знайти четверту його вершину D при умові, що основа АD в п’ять разів більша за основу ВС . ( Відповідь: D(8;-18) )
Дано трикутник АВС: А(4;1), В(7;5), С(-4;7 ). Знайти довжину бісектриси АD кута А. ( Відповідь:

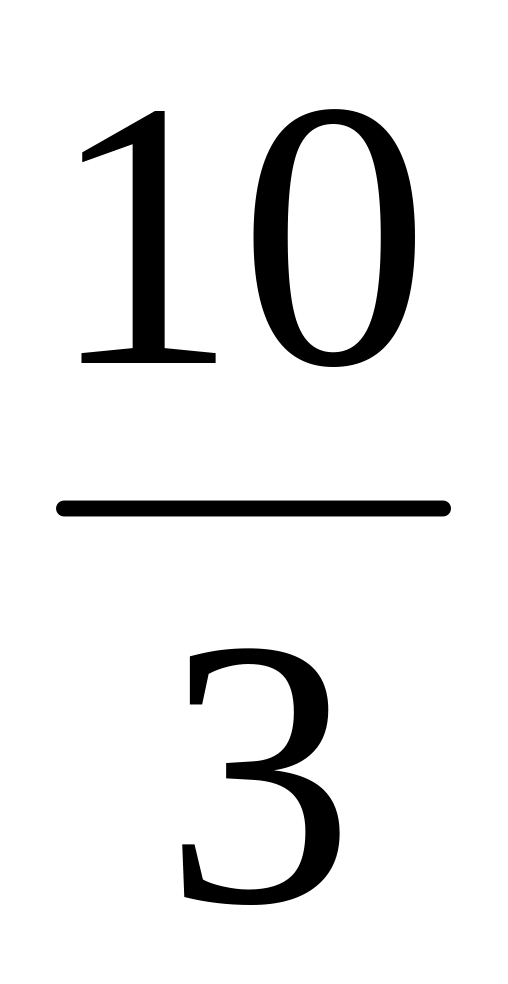
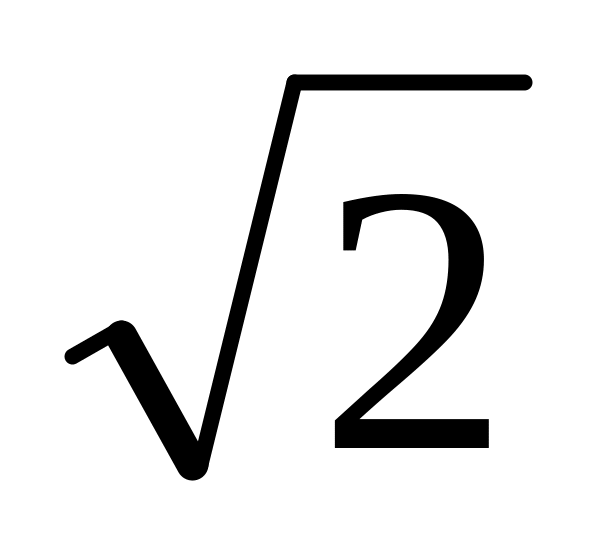 )
)Знайти центр ваги дротяного трикутника, довжина сторін якого 3, 4 і 5см. (Відповідь: якщо направити вісь абсцис по меншому із катетів, а вісь ординат по більшому, то для координат центр ваги трикутника отримаємо числа х=1 , у =
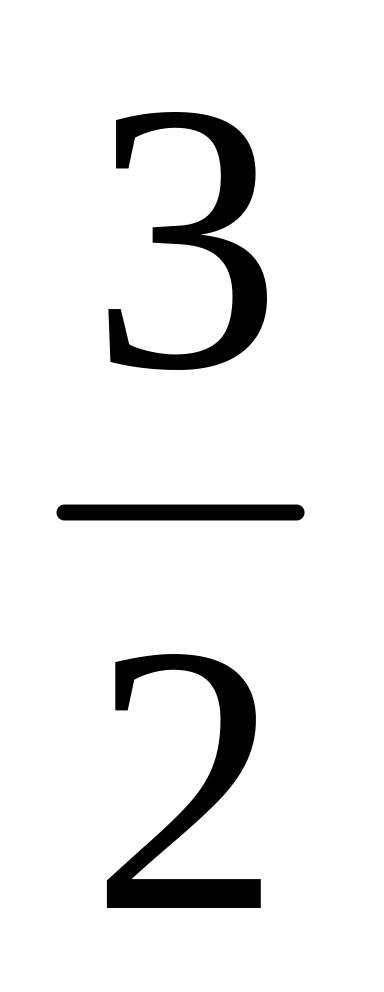 .)
.)Площа трикутника S=3, дві його вершини точки А(3;1) і В(1;-3), центр ваги цього трикутник лежить на осі Ох. Визначити координати третьої вершини С. ( Відповідь: (5;2) або(2;2) )
Знайти відстань між двома даними точками:
1) А(2;![]() ) і В (1;
) і В (1;![]() ) ;
) ;
2) С(4;
![]() ) і D (6;
) і D (6;
![]() )
;
)
;
3) Е (3;![]() ) і F (4;
) і F (4;![]() ).
(Відповідь: 1) АВ=
).
(Відповідь: 1) АВ=![]() ;
2)СD=10; 3)EF=5. )
;
2)СD=10; 3)EF=5. )
Знайти площу трикутника, одна із вершин якого розташована в полюсі, а дві інші мають полярні координати (4; ), (1;
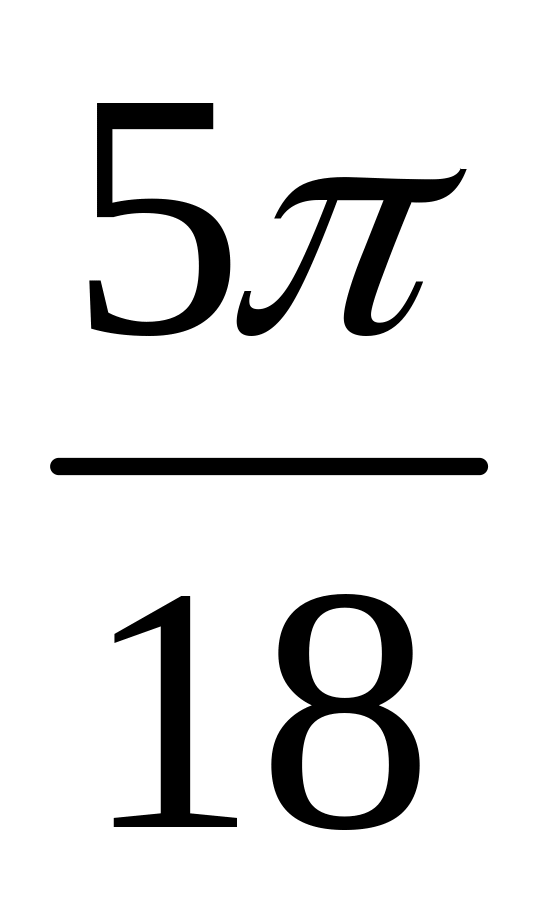 ). (Відповідь: S=1.)
). (Відповідь: S=1.)Знайти прямокутні координати точок, що задані своїми полярними координатами: А(2,
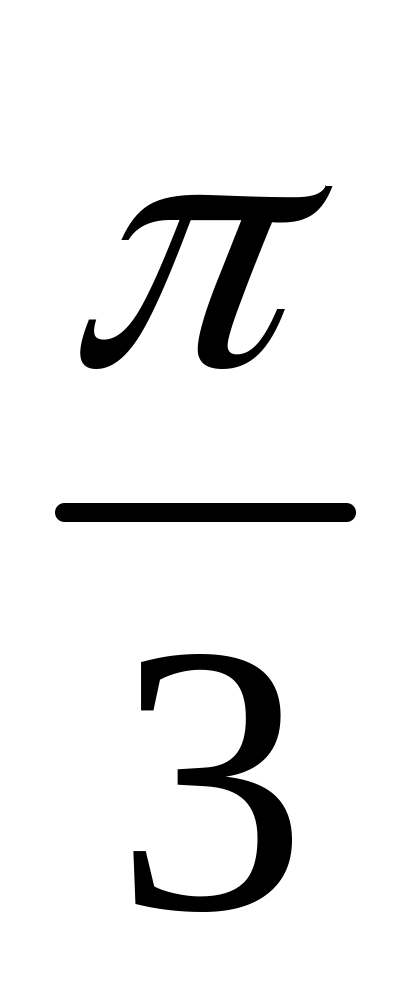 ),
В(
),
В(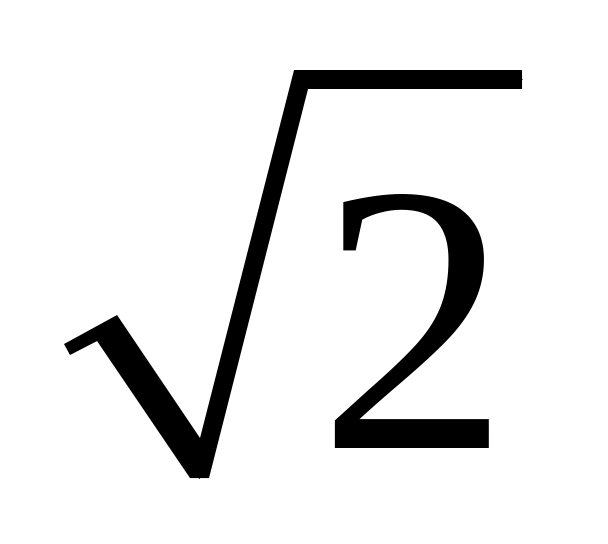 ,
,
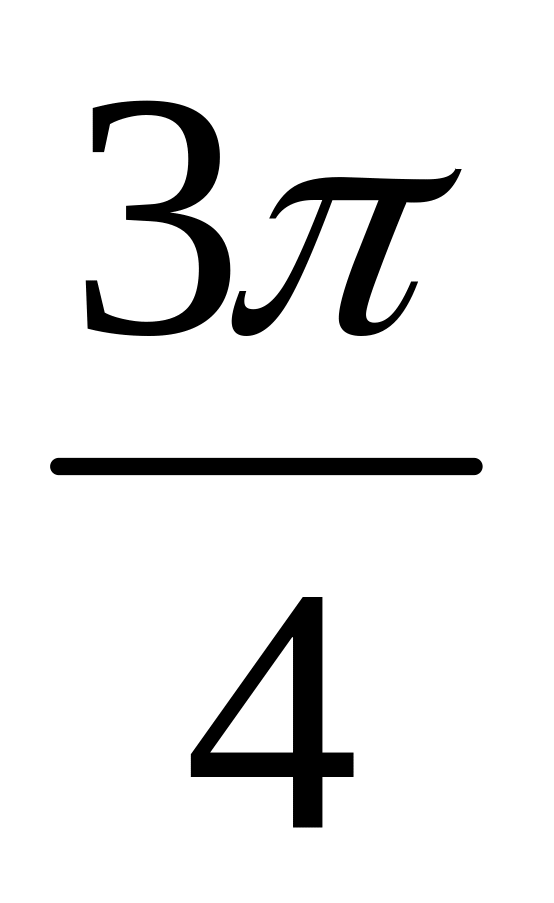 ),
С(5,
),
С(5,
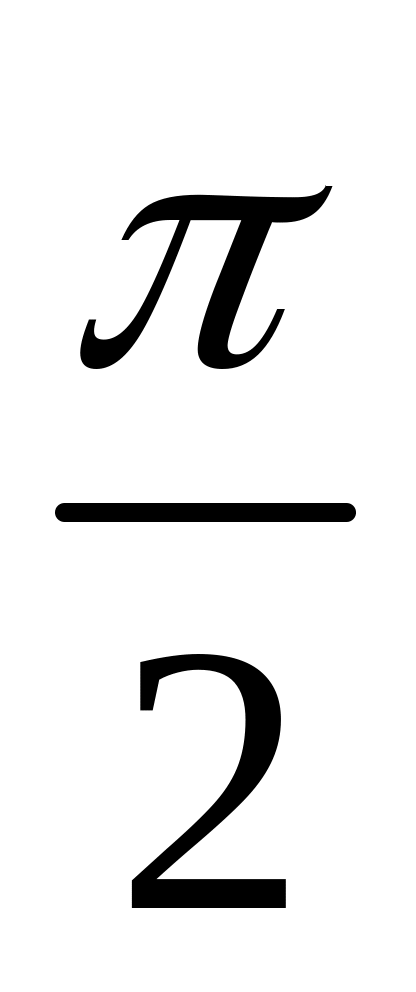 ),
D(3, -
),
D(3, -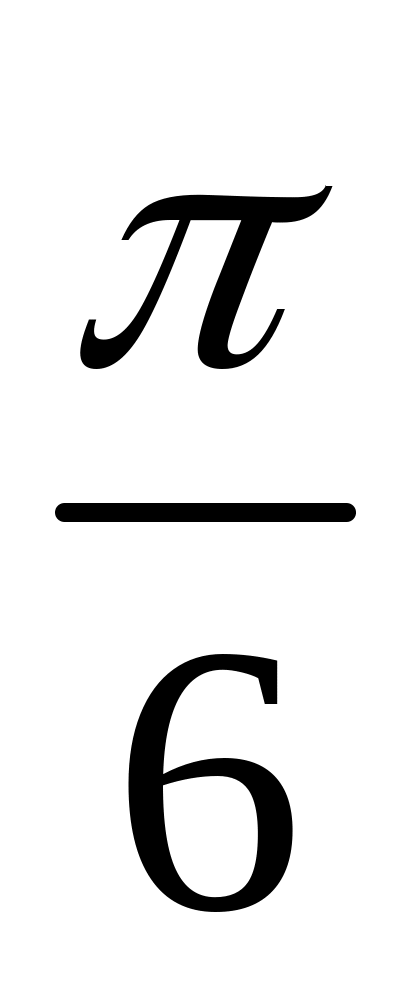 ),
причому вісь абсцис співпадає з полярною
віссю, а початок координат – з полюсом.
( Відповідь: А (1;
); В (-1;1); С(0;5); D (
),
причому вісь абсцис співпадає з полярною
віссю, а початок координат – з полюсом.
( Відповідь: А (1;
); В (-1;1); С(0;5); D (
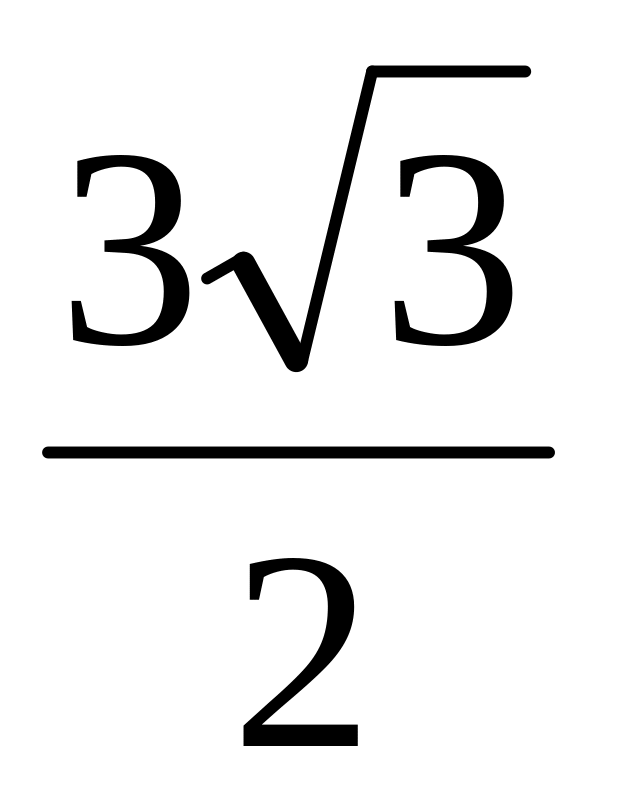 ;
-
)
).
;
-
)
).Знайти полярні координати точки М, знаючи її декартові координати х = 8, у = -6. ( Відповідь:
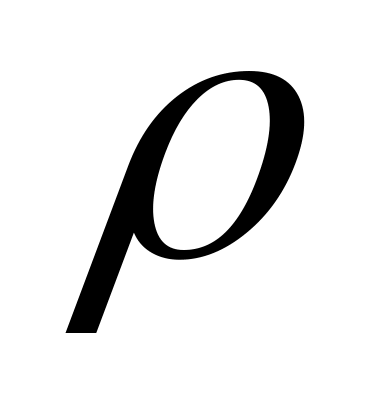 =
10, cosφ =
=
10, cosφ =
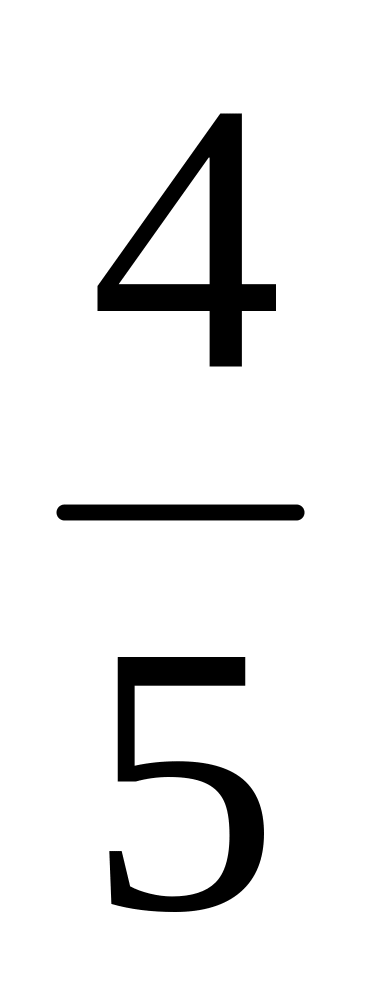 ,
sin φ = -
,
sin φ = - .)
.)Дано полярні координати точок А(8; -
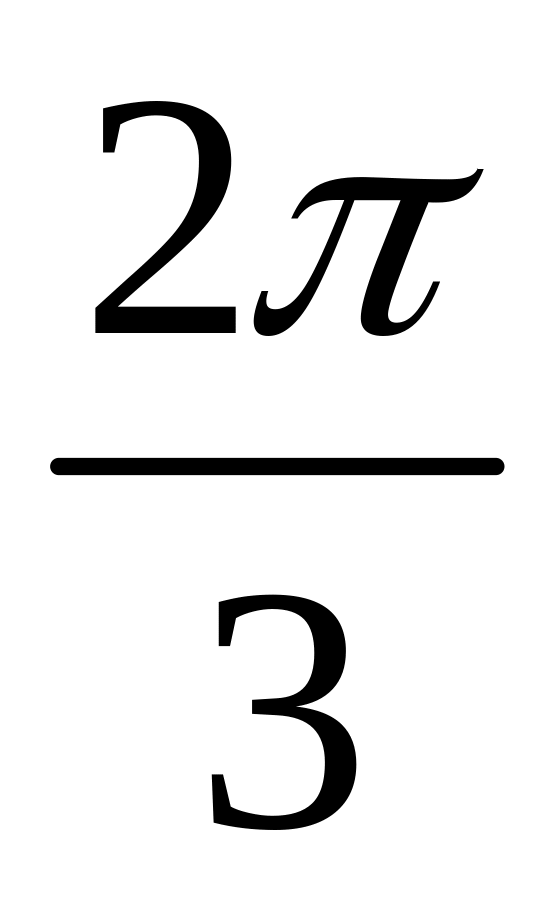 )
і В (6;
).
Знайти полярні координати середини
відрізка АВ. ( Відповідь: (1;-
)
).
)
і В (6;
).
Знайти полярні координати середини
відрізка АВ. ( Відповідь: (1;-
)
).Знайти площу п’ятикутника вершинами якого є точки А(-2;0), В(0;-1), С(2;0), D(3,2) та Е(-1:3). ( Відповідь: 12,5 )
В трикутнику АВС: А(5;-4), В(-1;2), С(5;1) проведена медіана АD. Знайти її довжину. ( Відповідь АD =
 ).
).Знайти дві точки А та В, знаючи що точка С(-5;4) ділить відрізок АВ у відношенні
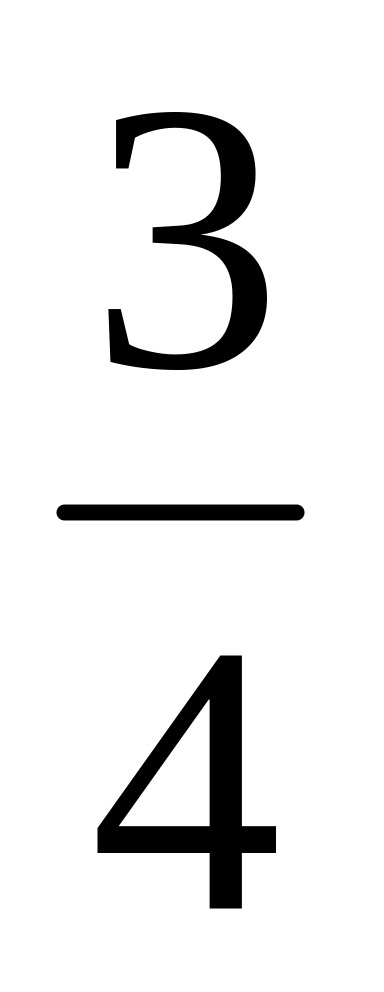 ,
а точка D(6;-5) - у відношенні
,
а точка D(6;-5) - у відношенні
 .
(Відповідь: А(160;-131), В(-225;184) ).
.
(Відповідь: А(160;-131), В(-225;184) ).Дано дві точки А (-4;2), В(8;-7). Знайти точки С і D, які ділять відрізок АВ на три рівні частини.
( Відповідь: С(0;-1), D(4;-4) ).
Вектори. Лінійні операції над векторами. Лінійна залежність векторів.
Точки
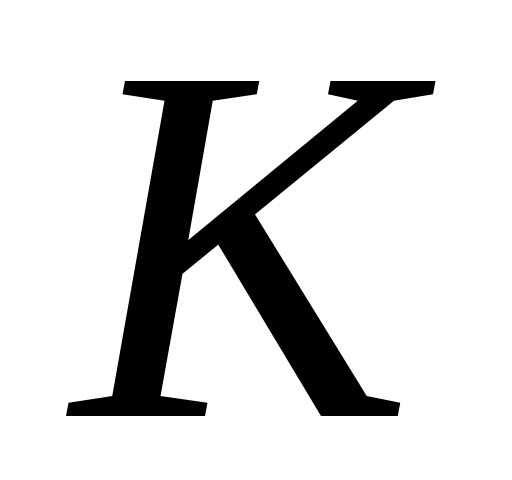 і
і
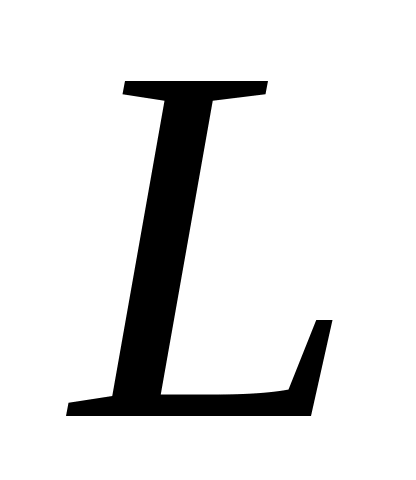 є серединами сторін
є серединами сторін
 і
і
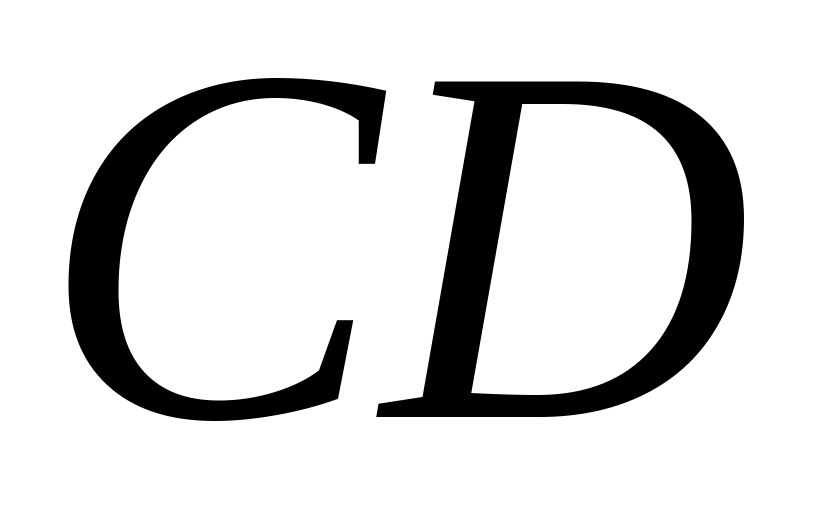 паралелограма
паралелограма
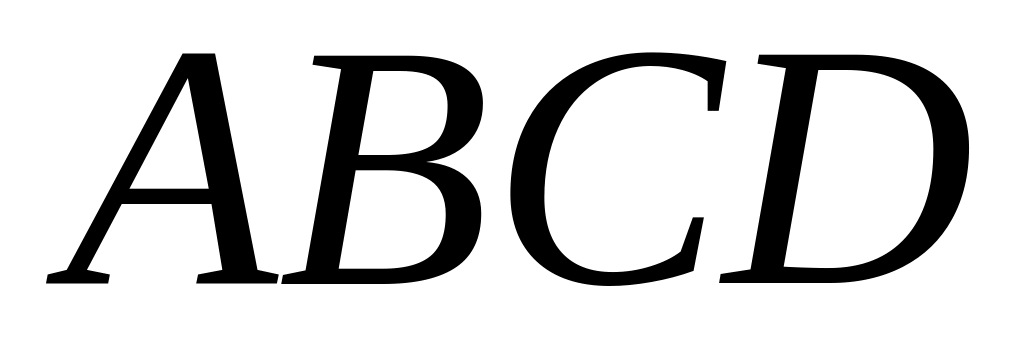 .
Позначивши
.
Позначивши
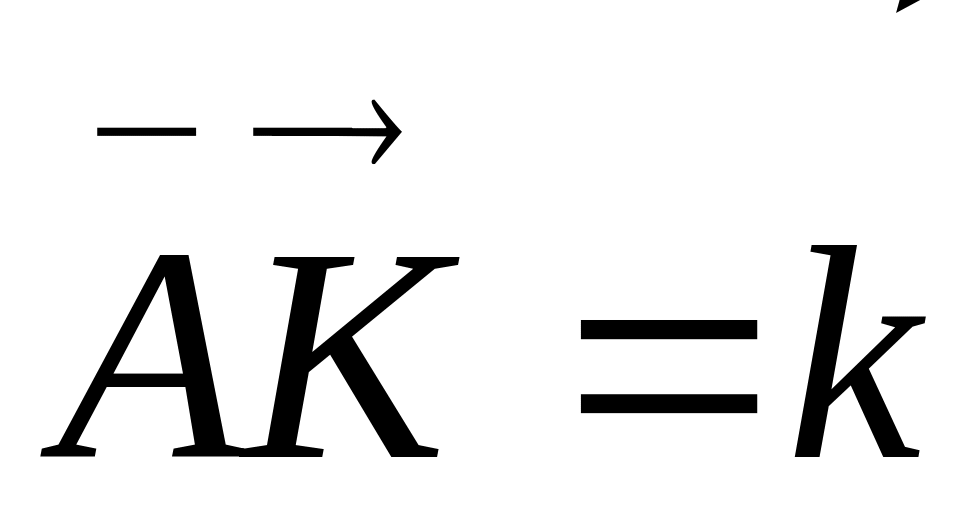 і
і
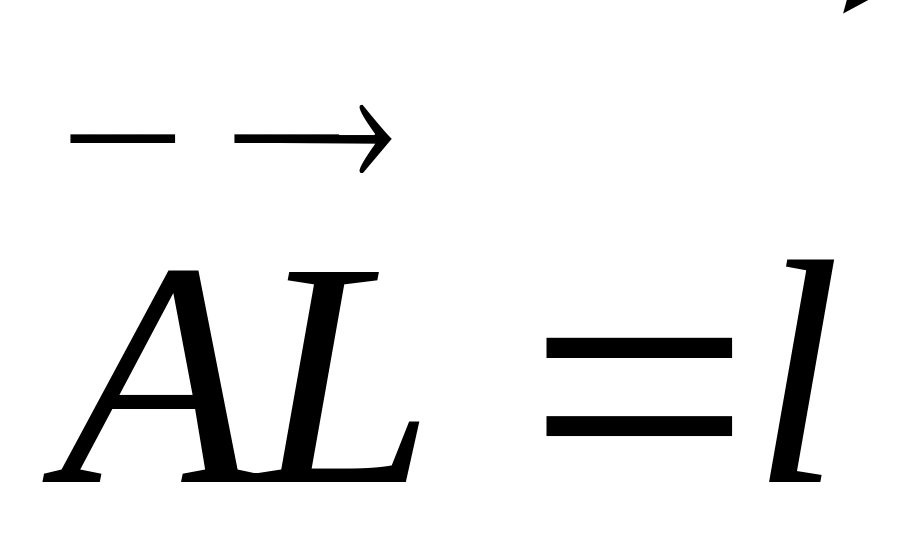 ,
виразити через вектори
,
виразити через вектори
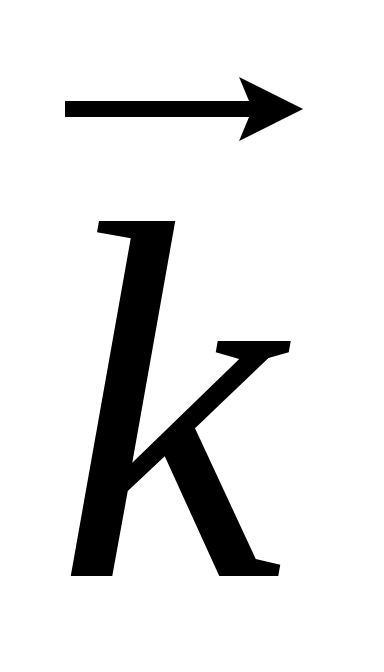 і
і
 вектори
вектори
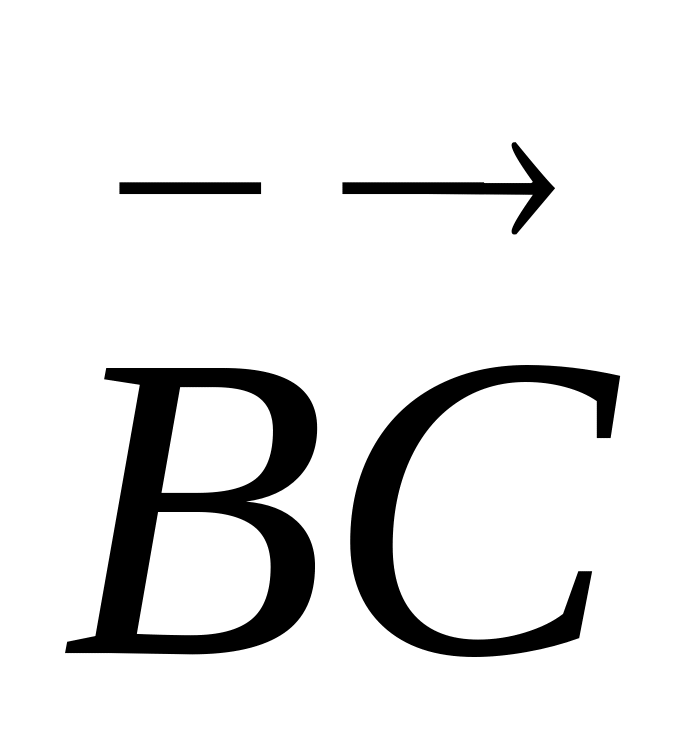 і
і
 .
.У трикутнику знайти точку, щоб сума векторів із цієї точки до вершин трикутника була рівна
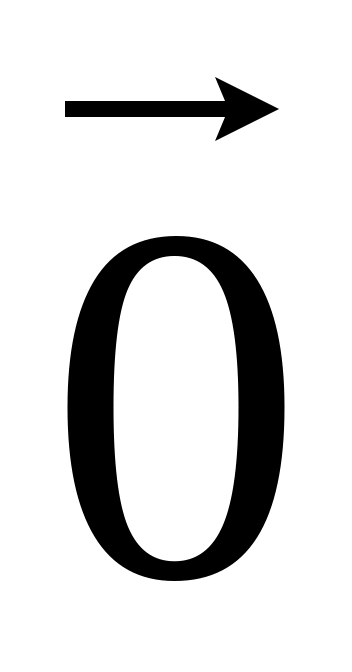 .
.Перевірити, які із векторів
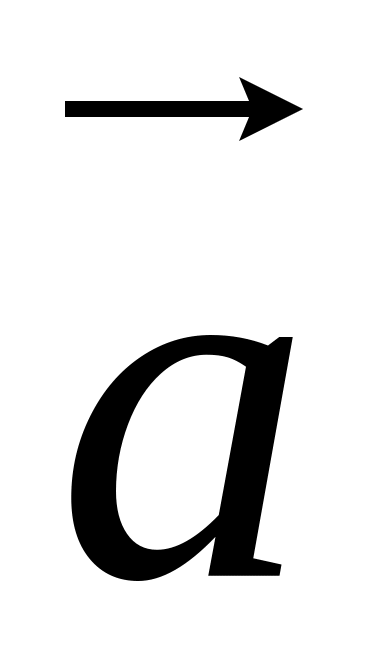 ,
,
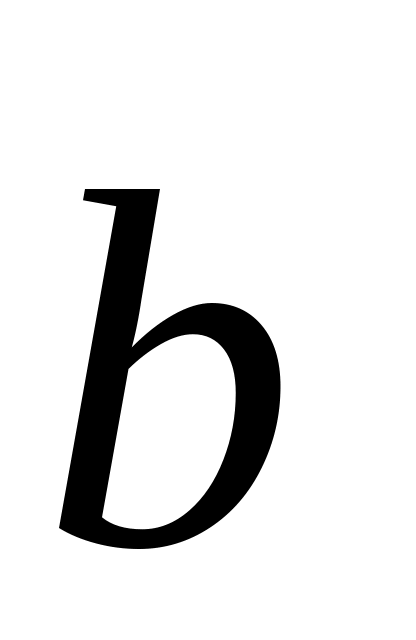 ,
,
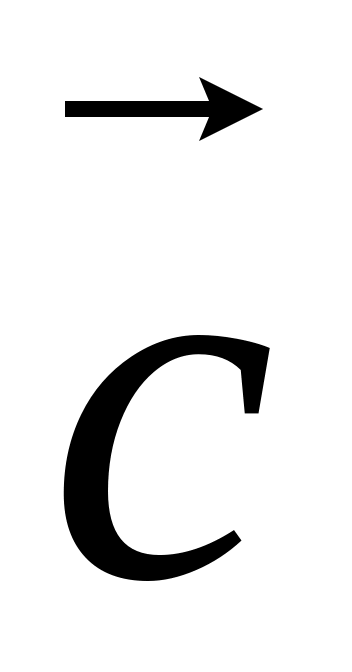 є лінійно залежні, у випадку, коли це
можливо, виразити вектор
через вектори
і
:
є лінійно залежні, у випадку, коли це
можливо, виразити вектор
через вектори
і
:
а)
![]() ,
,
![]() ,
,
![]() .
.
б)
![]() ,
,
![]() ,
,
![]() .
.
4.
Вектори
![]() =
=
![]() і
і
![]() =
=
![]() є діагоналями паралелограма АВСD.
Виразити через вектори
є діагоналями паралелограма АВСD.
Виразити через вектори
![]() і
вектори
і
вектори
![]()
![]() ,
,
![]() ,
,
![]() ,
які є сторонами цього паралелограми.
,
які є сторонами цього паралелограми.
(
Відповідь:
![]() =
=![]() ,
=
,
=![]() ,
,![]() =
=![]() ,
=-
,
=-![]() ).
).
5. В
трикутнику АВС проведені медіани АD,
ВЕ, і СF. Знайти суму векторів
![]() +
+![]() +
+![]() .
.
( Відповідь: 0 ).
6. В
чотирикутнику АВСD покладемо
![]() =
=![]() ,
=
,
=![]() ,
=
,
=![]() ,
,
![]() =
=![]() .
Знайти вектор
.
Знайти вектор![]() ,
що з’єднує середини діагоналей АС і
ВD.
,
що з’єднує середини діагоналей АС і
ВD.
(
Відповідь:
=![]() -
-
![]() ).
).
7.
Дано три вектора
![]() ,
,
![]() ,
,
![]() .
Підібрати числа
.
Підібрати числа
![]() і
і
![]() так щоб три вектори
так щоб три вектори
![]() ,
,
![]() та
та
![]() утворювали трикутник, якщо початок
вектора
співпадає з кінцем вектора
,
а початок вектора
з кінцем вектора
.
утворювали трикутник, якщо початок
вектора
співпадає з кінцем вектора
,
а початок вектора
з кінцем вектора
.
(
Відповідь:![]() =2,
=2,
![]() =-3
).
=-3
).
8. Із однієї точки проведені вектори =(-12;16), = (12;5). Знайти координати одиничного вектора, який будучи проведений із тієї ж точки, ділив би кут між та навпіл.
(
Відповідь (![]() ;
;
![]() )
).
)
).
9.
Показати, що які б не були три вектора
,
та
![]() і три числа λ, μ, γ, вектори λ
-μ
,
γ
- λ
,
μ
-γ
компланарні.
і три числа λ, μ, γ, вектори λ
-μ
,
γ
- λ
,
μ
-γ
компланарні.
10.Відносно ортонормованого базису дано вектор =(-8;4;1). Знайти одиничний вектор, який має такий напрямок, що і вектор .
(
Відповіді: (-![]() ;
;![]() ;
;![]() )).
)).
11.Дано вектор =(6;-8). Знайти координати одиничного вектора, який колінеарний з і напрямлений 1) в ту сторону; 2) в протилежну.
( Відповідь: ( 0;6;-0;8), (-0;6;0;8) ).
12. В
трикутнику АВС проведена бісектриса
АD кута А. Виразити вектор
через вектори
і
![]() .
.
(
Відповідь:
![]() =
=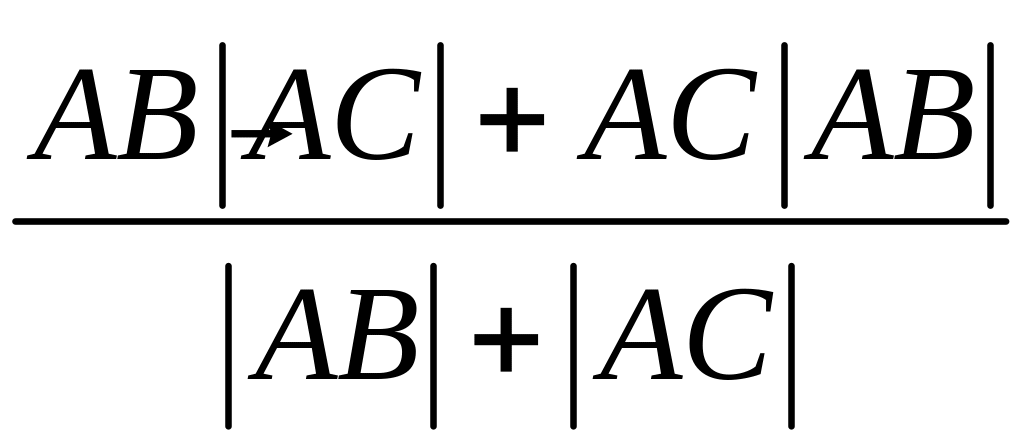 ).
).
13.Представити
вектор
![]() як лінійну комбінацію векторів
,
і
у випадках:
як лінійну комбінацію векторів
,
і
у випадках:
1)
=(2;3;1),
=(5;7;0),
=(3;-2;4),
![]() =(4;12;-3)
=(4;12;-3)
2) =(5;-2;0), =(0;-3;4), =(-6;0;1), =(25;-22;16)
( Відповідь: 1) = + - , 2) =5 +4 ).
14.Знаючи
радіус – вектори
![]() вершин трикутниказнайти
радіус – вектор точки перетину його
медіан.
вершин трикутниказнайти
радіус – вектор точки перетину його
медіан.
(
Відповідь:
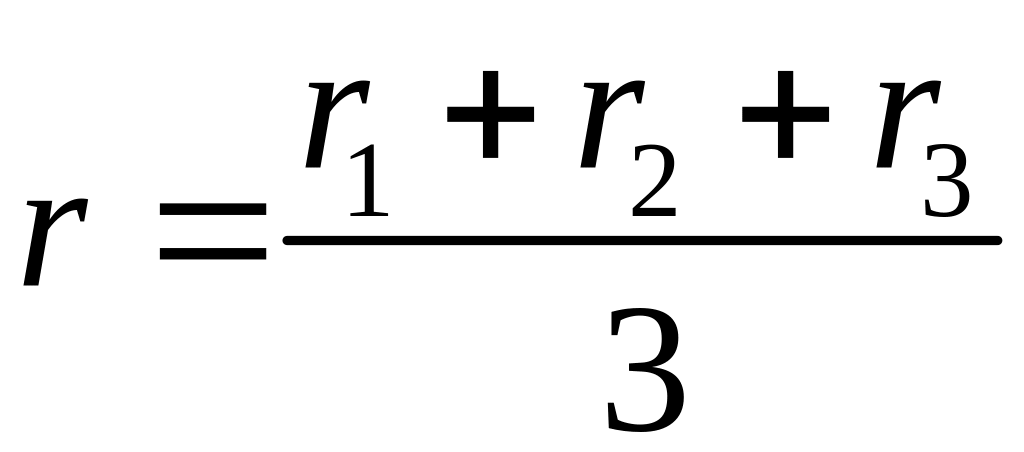 ).
).
Скалярне, векторне та мішане множення векторів.
В вершині куба прикладено три сили, різні за величиною 1, 2 і 3 і напрямлені по діагоналях граней куба. Визначити величину рівнодійної. (відповідь: 5).
Вектори
 і
визначені координатами своїх кінців:
і
визначені координатами своїх кінців:
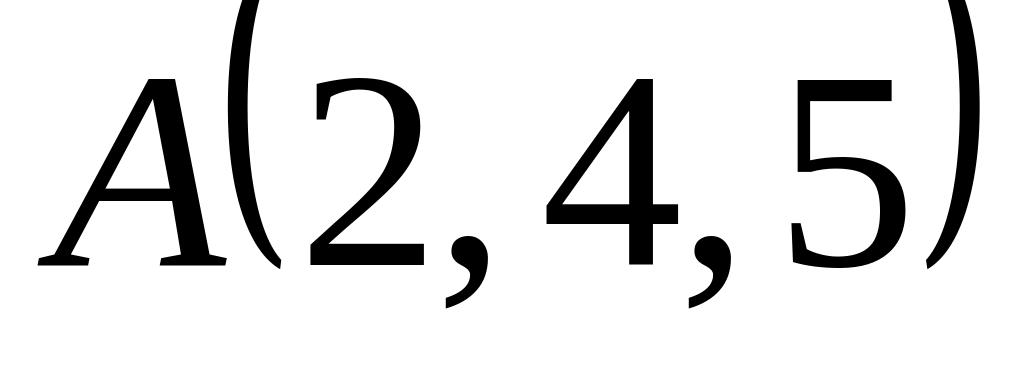 ;
;
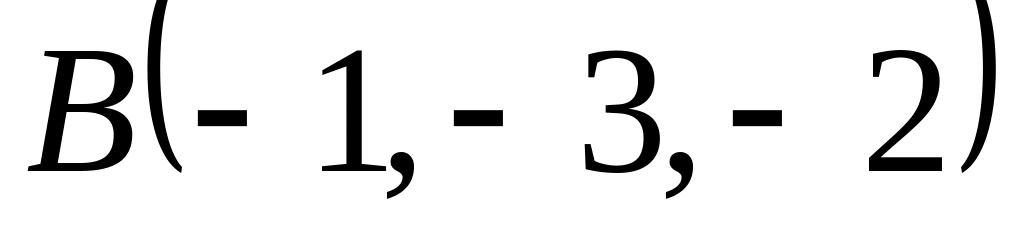 ;
;
 ;
;
 .
.
Знайти а) векторний
добуток
![]() ;
;
б) його модуль;
в) напрямні косинуси векторного добутку
(Відповідь: а) ![]() ,
,
б) ![]() ,
,
в) ![]() ).
).
Знайти площу трикутника, координати вершин якого відомі
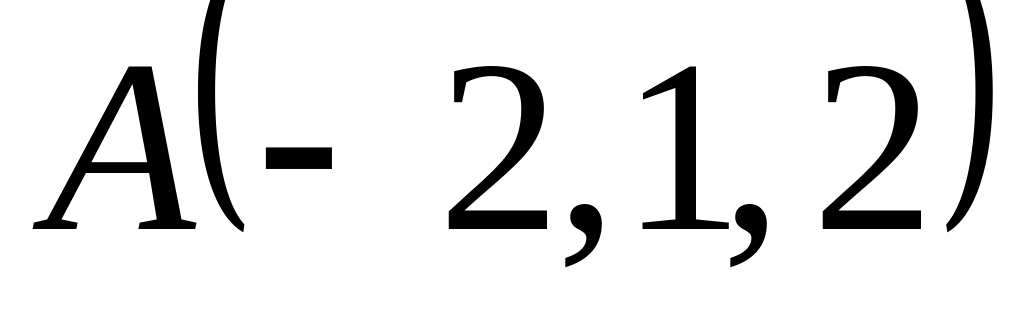 ;
;
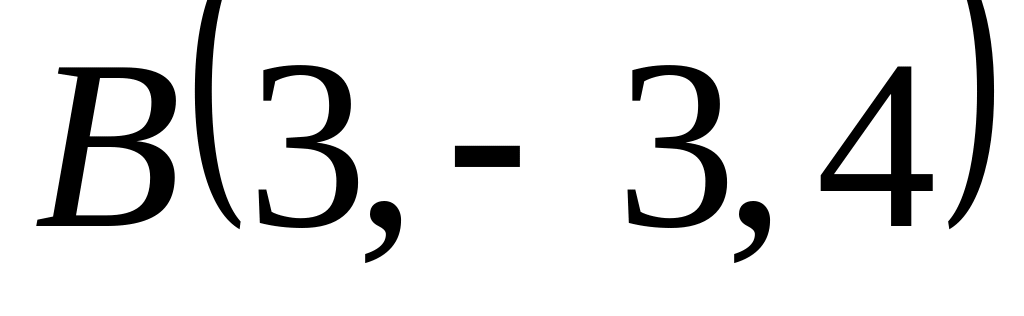 ;
;
 .
.
(Відповідь:
![]() кв.од.).
кв.од.).
Знайти об’єм піраміди за відомими координатами її вершин:
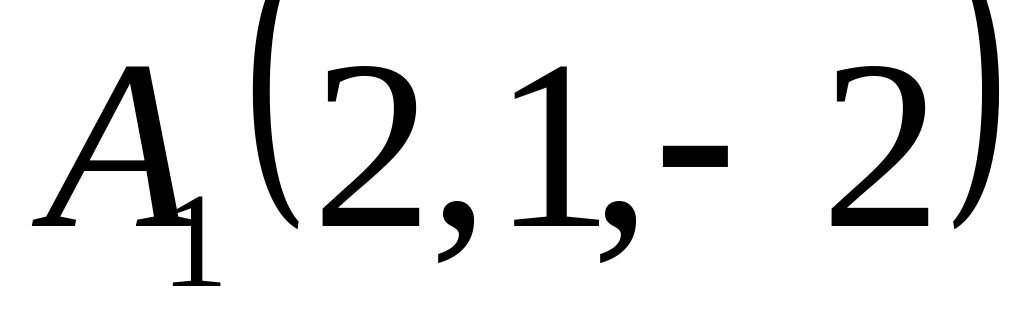 ,
,
 ;
;
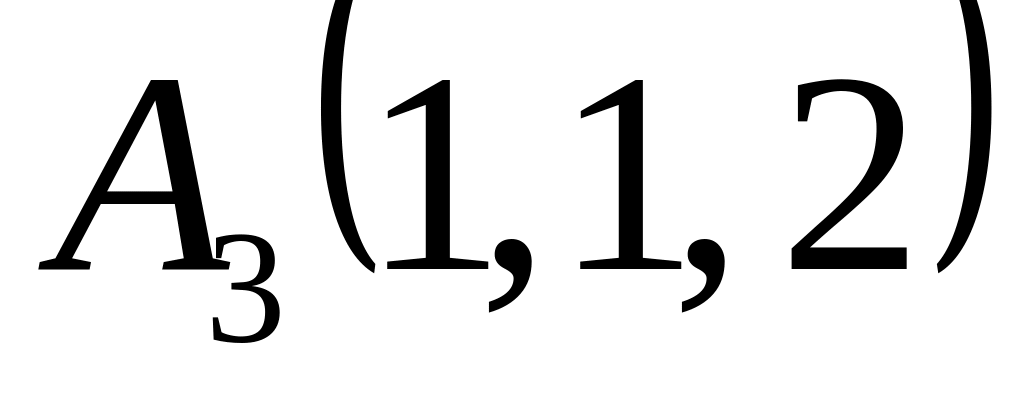 ;
;
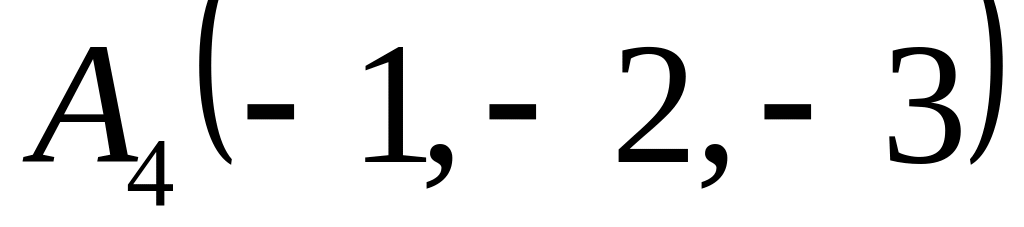 .
.
(Відповідь:
 куб.од.).
куб.од.).
Дано вектори
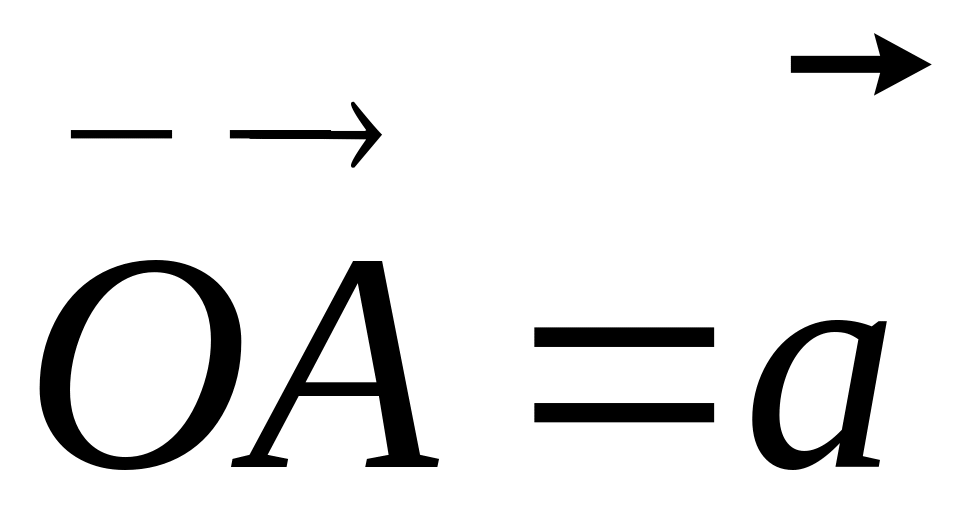 ,
,
 ,
,
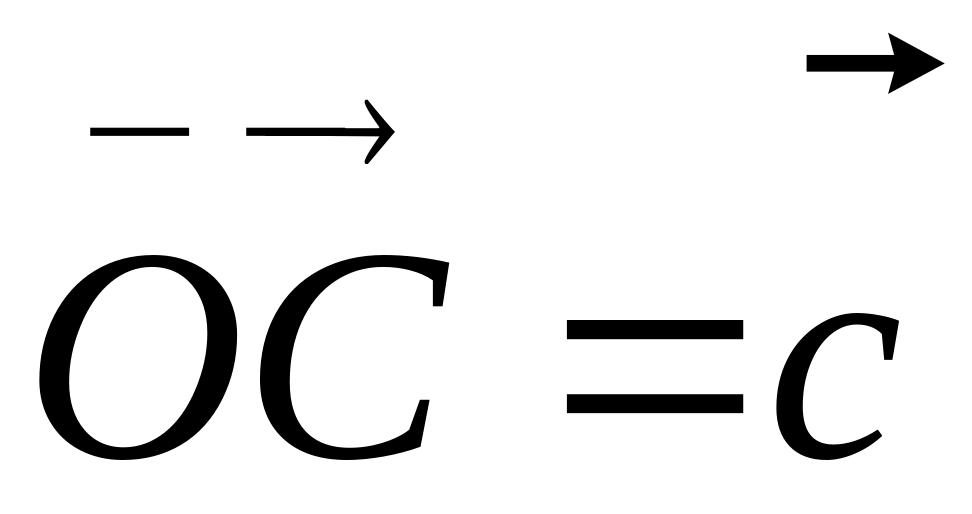 .
Вектори
і
.
Вектори
і
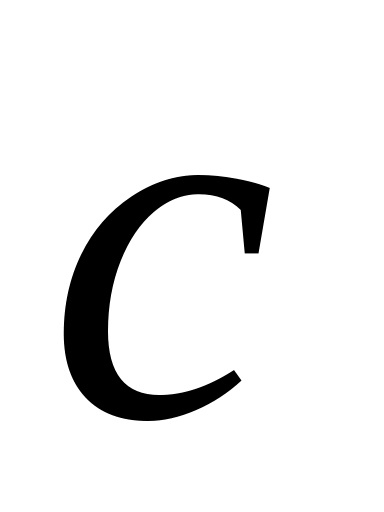 не колінеарні. Нехай
не колінеарні. Нехай
 – проекція точки
– проекція точки
 на площину
на площину
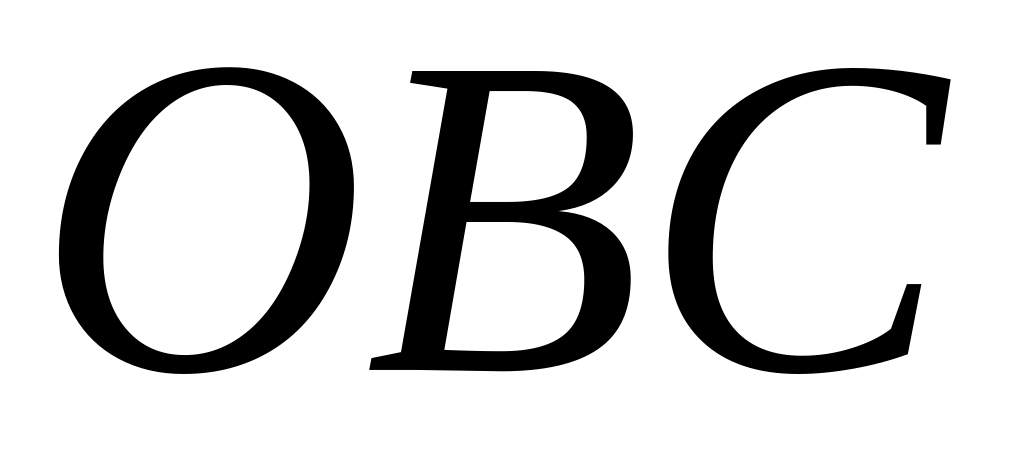 .
Найти вектор
.
Найти вектор
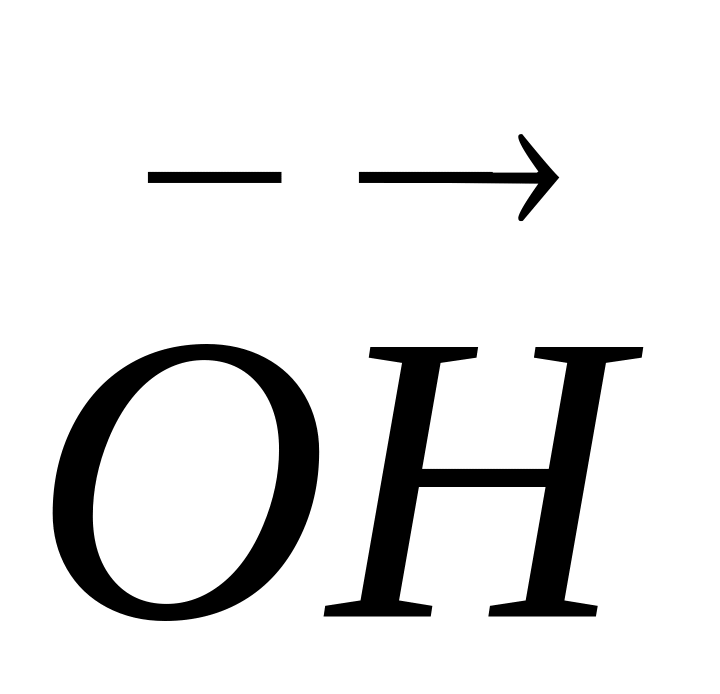 .
.
(Відповідь:
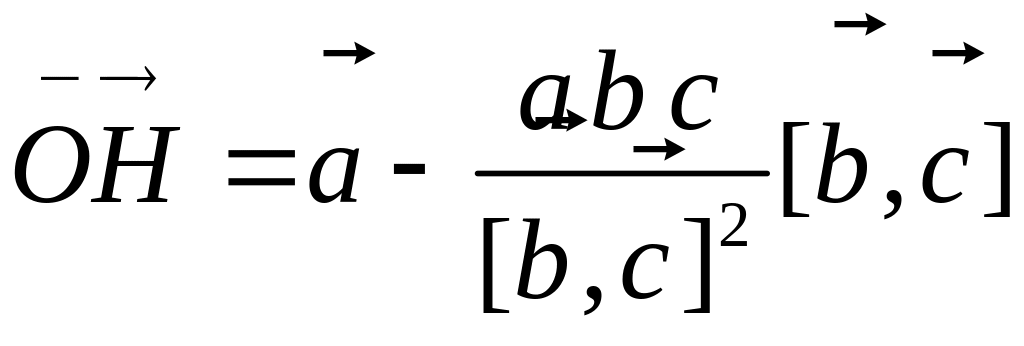 ).
).
Знайти скалярний добуток векторів та у випадку
1) | |=| |=1, ( ,^ )=1350;
2)
|
|=3,
|
|=1
а![]()
![]() в.
в.
(
Відповідь: 1) -![]() ;
2) -3) ).
;
2) -3) ).
В трикутнику АВС дано довжини його сторін ВС=5, СА=6, АВ=7, Знайти скалярний добуток векторів
 і
і
( Відповідь -19 ).
Який кут утворюють одиничні вектори
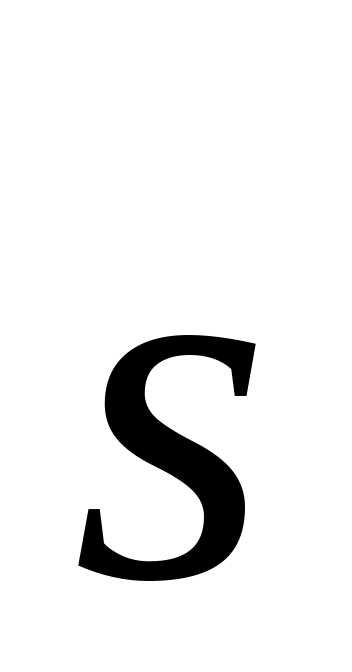 та
та
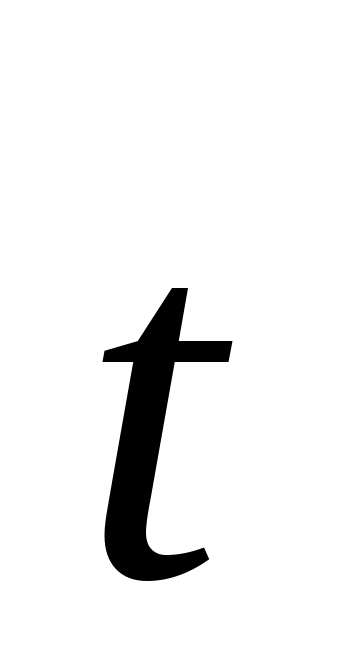 ,
якщо відомо, що вектори
=
,
якщо відомо, що вектори
= +2
+2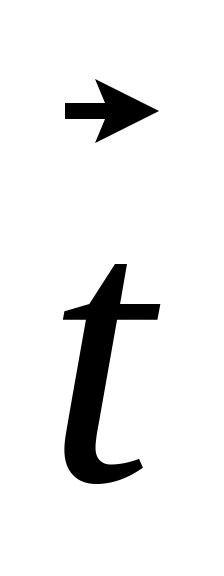 і
=5
і
=5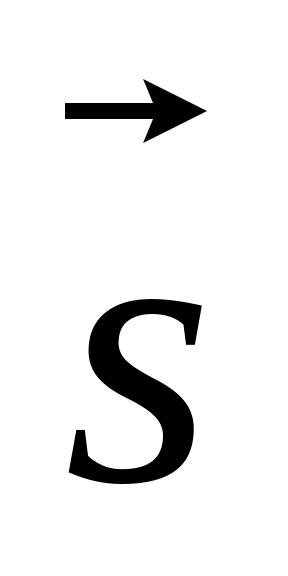 -4
взаємно –перпендикулярні.
-4
взаємно –перпендикулярні.
(Відповідь:
![]() ).
).
Знайти числову величину проекції вектора ( 7;-4) на вісь, паралельну вектору (-8;6).
( Відповідь: -8 )
Дано три вектори =(3;-2;4), =(5;1;6), =(-3;0;2). Знайти вектор
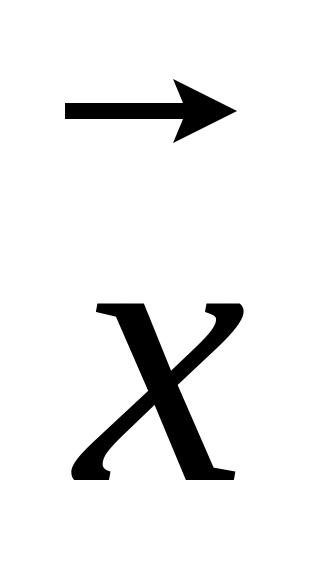 ,
що задовольняє одночасно трьом рівнянням
,
що задовольняє одночасно трьом рівнянням
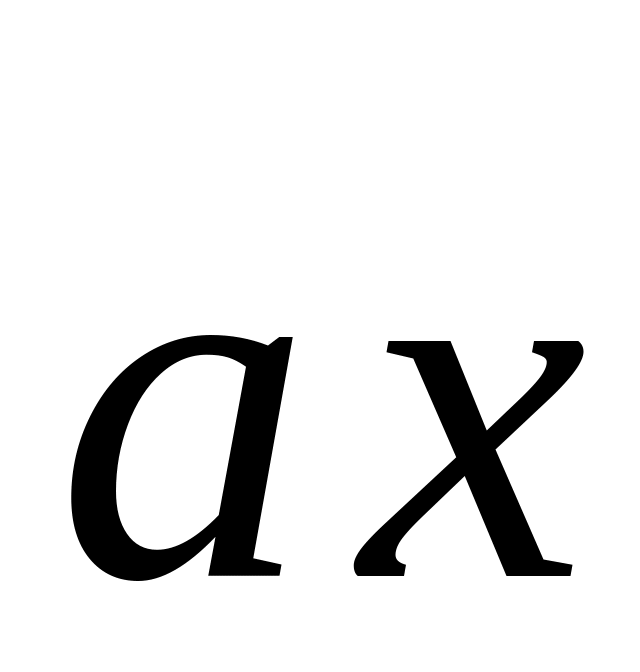 ·=4,
·=4,
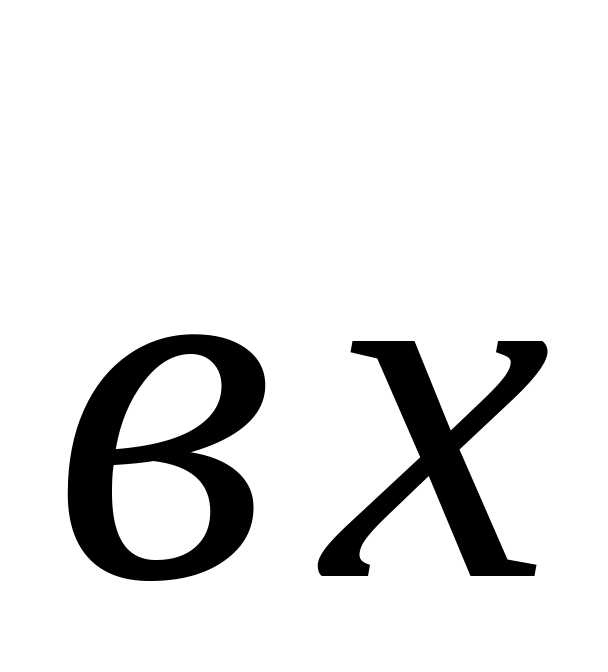 =35,
=35,
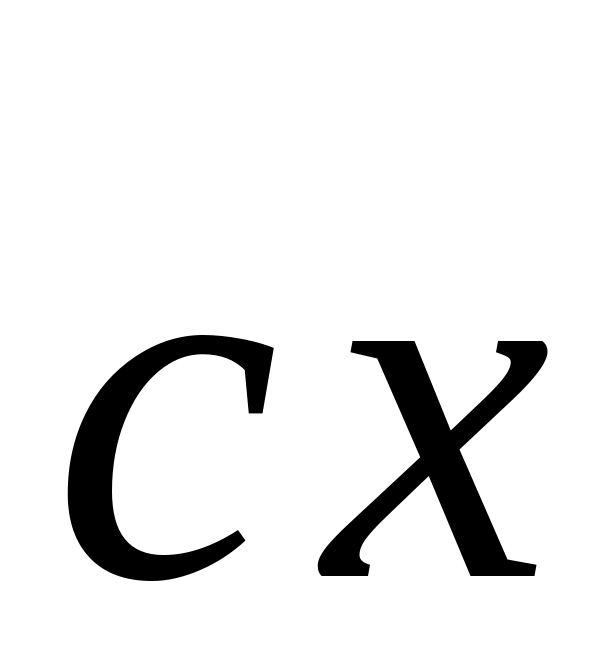 =0.
=0.
(Відповідь:
![]() =(2;7;3) ).
=(2;7;3) ).
Дано два вектора =(11;10;2) та =( 4;0;3). Знайти вектор
 , перпендикулярний до векторів
та
рівний 1 і напрямлений так, щоб трійка
векторів
,
,
була орієнтована так як трійка одиничних
векторів ортонормованого базису.
, перпендикулярний до векторів
та
рівний 1 і напрямлений так, щоб трійка
векторів
,
,
була орієнтована так як трійка одиничних
векторів ортонормованого базису.
(Відповідь:
(![]() ; -
; -![]() ; -
; -
![]() )
).
)
).
Знайти площу паралелограма, побудованого на векторах =(8;4;1), =(2;-2;1).
(Відповідь: 18 ).
Дано вектори =(3;1;2), =(2;7;4), =(1;2;1).
Знайти: 1) ; 2) ( [ ] с); 3) ( [ ] ).
(Відповідь: 1) -7; 2) (-46,29,-12); 3) (-7,7,7)).
Визначити кут λ між векторами та , що задані своїми координатами: 1) =(4,3), =(1;7); 2) =(6;-8), =(12;9), 3) =(2;5), =(3,-7).
(Відповідь: 1) 450, 2) 900, 3)1350).
