3.9. Мощность в цепях синусоидального тока
Имеется пассивный двухполюсник (рис. 3.38), схема которого содержит все элементы (индуктивные, емкостные и резистивные).
На зажимы приложено
синусоидальное напряжение
и протекает
синусоидальный ток
.
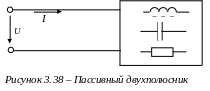
3.9.1. Мгновенная мощность
Мгновенной
мощностью называют
произведение u
на i:
.
Т.е.
,
где
– сдвиг по
фазе между током и напряжением, т.е. угол
.
Выражение для
мгновенной мощности представляет собой
сумму постоянной составляющей
и переменной
с удвоенной частотой
.
Вычертим график
мгновенных значений
(рис. 3.39):
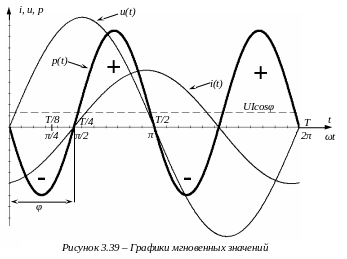
Знак мгновенной мощности меняется в зависимости от знаков тока i и напряжения u. Мгновенная мощность р будет отрицательна, когда знаки напряжения и тока различны (рис. 3.39). Если ток и напряжение имеют одинаковые знаки, то значение мгновенной мощности положительное. Из графика р(t) видно, что он имеет постоянную составляющую.
3.9.2. Активная мощность
Активной мощностью называют среднее значение мгновенной мощности за период:
.
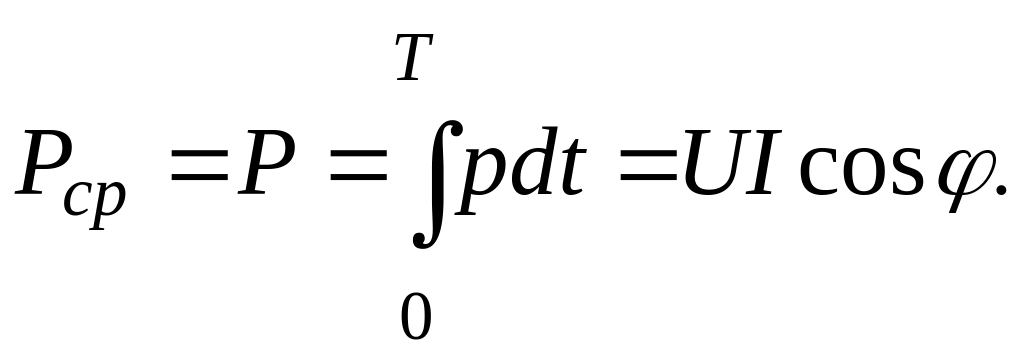Произведение тока на напряжение называют полной мощностью S:
.
Следовательно, активная и полная мощности связаны соотношением:
.
Активная мощность измеряется в ваттах - [Вт], а полная мощность в вольт-амперах - [ВА].
В общем случае
активную мощность можно определить,
используя активную составляющую
напряжения и тока:
,
где
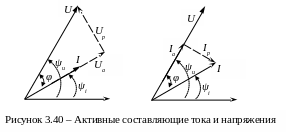
- активная составляющая напряжения
(рис. 3.40, а),
- активная составляющая тока
(рис. 3.40, б).
Активная мощность в электрических схемах выделяется в виде тепла на резистивных элементах или создает полезную мощность потребителей. Такими могут быть вращающий момент электродвигателя и др. Для электрических схем переменного тока, имеет место баланс активных мощностей:
.
Для разветвленных
электрических цепей с несколькими
источниками питания, необходимо
рассчитывать активную мощность каждого
источника питания. В этом случае угол
,
будет указывать сдвиг по фазе между
напряжением и током на зажимах каждого
источника. Тогда баланс активных
мощностей для разветвленных электрических
цепей будет иметь вид:
.
В разветвленных
цепях с несколькими источниками питания,
для некоторых источников, возможно,
получить значение активной мощности
с отрицательным знаком (
при
).
Это означает, что данный источник не
генерирует активную мощность, а
потребляет. Например, электрические
машины переменного тока могут работать
в качестве электродвигателя переменного
тока (потребляют электрическую энергию)
и генераторов переменного тока (генерируют
электрическую энергию).
3.9.3. Реактивная мощность
Реактивной
мощностью
,
называют
мощность, равную
.
Ее
величина идет на создание энергии
магнитного поля
катушки
индуктивности и
электрического поля
конденсаторов. В электрических схемах,
содержащих индуктивности и емкости,
происходит обмен энергией магнитного
поля катушки и электрического поля
конденсаторов. Если реактивная энергия
,
идущая на создание магнитного поля
катушки, больше энергии электрического
поля конденсаторов
(ток отстает от напряжения на угол φ),
то
и
реактивная мощность принимается с
положительным знаком, и наоборот.
Реактивная мощность измеряется в вольт-ампер реактивный - [ВАр].
В общем случае
реактивную мощность можно определить,
используя реактивную составляющую
напряжения и тока:
,
где
- реактивная составляющая напряжения
(рис. 3.40, а),
- реактивная составляющая тока
(рис. 3.40, б).
Для электрических схем переменного тока, имеет место баланс реактивных мощностей:
.
Баланс реактивных мощностей для разветвленных электрических цепей с несколькими источниками питания, имеет вид:
.
Реактивная
мощность расходуется на создание энергии
магнитного поля катушки или энергии
электрического поля конденсатора. Она
имеет положительный знак, если
.
Из
вышеуказанного следует, что
.