Для получения комплекса эдс направляем по оси действительных чисел.

2. Опыт короткого замыкания (рис. 3.74). В результате проведения опыта, измеряем (А).

По результатам опытов холостого хода и короткого замыкания, определяем величину полного (входного) сопротивления:

(Ом).

3. Опыт короткого замыкания с дополнительной емкостью (рис. 3.75) С=20 (мкФ) (R_С=159,3 Ом). В результате проведения опыта, измеряем (А).

По результатам опытов холостого хода и короткого замыкания с дополнительной емкостью, определяем величину полного (входного) сопротивления:

(Ом).

Определяем активные и реактивные составляющие входных сопротивлений

(Ом).

3.12. Резонансные явления в электрических цепях

Д опустим, имеется двухполюсник (рис. 3.72), содержащий индуктивные, емкостные и резистивные элементы, к зажимах которого приложено синусоидальный и протекает синусоидальный ток .

Резонанс в цепи имеет место, когда _u = _i, т.е.  = 0. Следовательно, из сети потребляется только активная мощность - , так как . Входные сопротивления или проводимости, имеют чисто активный характер ; .

3.12.1. Резонанс напряжений

Резонанс напряжений наблюдается в цепях синусоидального тока с последовательным соединением r, L, C (рис. 3.73), по которым протекает синусоидальный ток .

Согласно условию резонанса: , т.е. .

Следовательно, условие резонанса напряжений для последовательного контура имеет вид:

Резонанс можно достичь, регулируя величины L и С, а при фиксированных значениях L и С результат можно достичь, регулируя частоту. Частота ω₀, при которой наступает резонанс, соответственно равна: .

Индуктивное или емкостное сопротивления при резонансе называются характеристическим сопротивлением равным .

При резонансе полное сопротивление равно активному сопротивлению:

.

Тогда из закона Ома следует: .

Напряжение на емкости и индуктивности равно: .

Добротностью контура называется отношение напряжения на индуктивности (или емкости ) к напряжению U на зажимах цепи:

.

Рассмотрим энергетические процессы цепи при резонансе. Энергия магнитного поля катушки индуктивного элемента при синусоидальном токе , равна .

Напряжение на емкости . Тогда энергия электрического поля конденсатора .

Суммарная энергия . Принимая во внимание, что 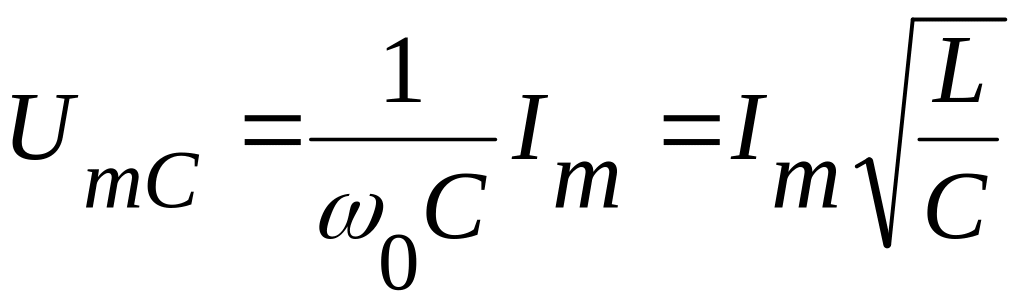, откуда и следовательно, , т.е. сумма энергий магнитного и электрического полей с течением времени не изменяется. Уменьшение энергии электрического поля сопровождается увеличением магнитного поля и наоборот. Таким образом, наблюдается непрерывный переход энергии из электрического поля конденсатора в магнитное поле катушки и наоборот.

Энергия, поступающая в цепь от источника питания, в любой момент времени полностью переходит в тепло. Поэтому для источника питания вся цепь эквивалентна одному активному сопротивлению.

3.12.2. Частотные характеристики последовательного контура

Зависимости параметров цепи от частоты ( ) называют частотными характеристиками, а зависимости действующих или амплитудных значений тока и напряжения от частоты – резонансными кривыми ( ), или амплитудно-частотными характеристиками.

Рассмотрим частотные характеристики пассивных элементов z(), x(), x_L(), x_C(). Для их оценки принимаем во внимание, что , и . На рисунке 3.74, изображены частотные характеристики.

Проанализируем частотные характеристики:

1. При 0<<_о – полное сопротивление имеет емкостной характер.

2. При  = _о – полное сопротивление имеет активный характер (резонанс).

3. При _о<<  – полное сопротивление имеет индуктивный характер.

Рассмотрим амплитудно-частотную характеристику I().

Для оценки I(), воспользуемся выражением

.

Зависимость выражения представлена на рисунке 3.75.

Проанализируем частотные характеристики:

1. При  = 0 – I = 0 , так как при  → 0 х_С →∞ z→∞.

2. При 0 <<_о – по мере увеличения частоты реактивное сопротивление х_С уменьшается, следовательно, полное реактивное сопротивление х уменьшается, полное сопротивление z уменьшается и ток I возрастает

(x_C   x   z   I  ).

3. При  = _о – полное сопротивление минимальное z = r, следовательно, значение тока наибольшее: .

4. При  >_о – по мере уменьшения частоты (при x_L > x_C и при увеличении ) полное реактивное сопротивление х увеличивается, полное сопротивление z увеличивается и ток I убывает

( > _о x_L > x_C и если  , то x   z   I  ).

5. Если   , то I  0.

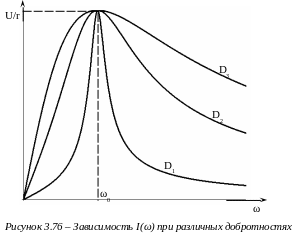
Оценим влияние добротности на форму кривой I().

При r = const  при всех добротностях. По мере увеличения добротности, график имеет более выраженный пик, т.е. перепад тока максимален.

На рисунке 3.76 приведены графики I() при различных добротностях (D₁ > D₂ > D₃).

Рассмотрим амплитудно-частотные характеристики U_L(), U_C().

Для оценки U_L(), воспользуемся выражением

Для оценки U_С(), воспользуемся выражением

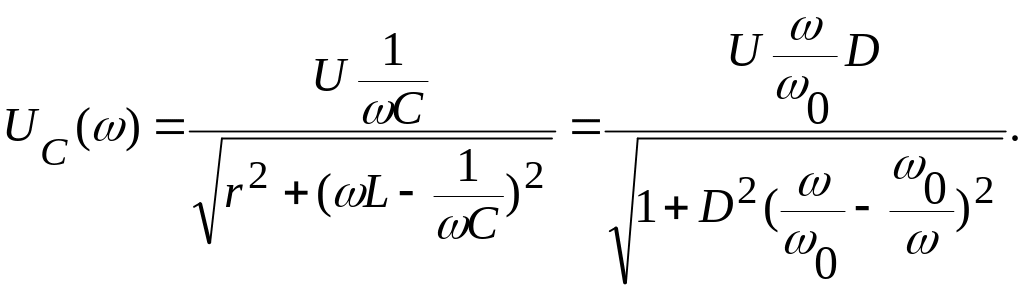
Зависимости выражений U_L() и U_C(), представлены на рисунке 3.77.

Проанализируем амплитудно-частотную характеристику U_L():

1. При  = 0 сопротивление x_L = 0, ток I = 0, и следовательно U_L = 0.

2. При изменении частоты 0 до ₀ сопротивление x_L увеличивается и ток I увеличивается, и следовательно U_L возрастает.

3. При дальнейшем увеличении частоты  > ₀, ток I уменьшается, но при за счет роста x_L напряжение U_L продолжает возрастать.

4. При частоте  = _L – кривая U_L () имеет максимум (U_L = U_max). Для определения _L и U_L() необходимо взять производную. Тогда имеем , .

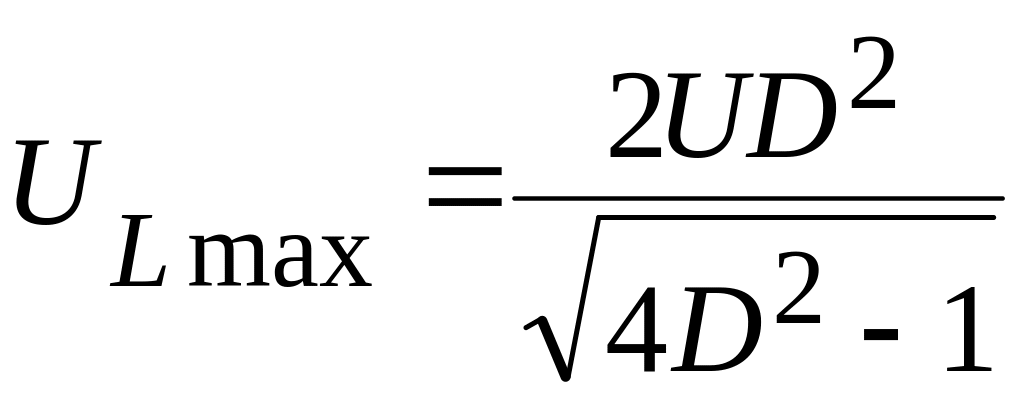5. При дальнейшем увеличении    – U_L  U, т.е. стремится к напряжению на зажимах сети.

Проанализируем амплитудно-частотную характеристику U_С():

1. При  = 0 ток I в цепи отсутствует, и следовательно U_С = U.

2. При изменении частоты 0 до ₀ сопротивление x_С уменьшается и ток I увеличивается, и следовательно U_С возрастает.

3. При частоте  = _С кривая U_С () имеет максимум (U_С = U_max). Для определения _С и U_С() необходимо взять производную. Тогда имеем , . Следовательно, .

4. При    – U_С  0, т.к. ток I и x_С равны нулю.

Возможен случай, когда кривые U_L () и U_C () не будут иметь экстремума. Это будет следовать из выражения _L и _С.

Если добротность _L и _С не являются действительными числами и на графике максимум отсутствует, а сами графики имеют монотонный характер, представленный на рисунке 3.78.