
- •Тема 1. Університетська освіта в системі Болонського процесу
- •2. Болонська конвенція передбачає трьохступеневу систему освіти.
- •3. Болонська конвенція передбачає прозорість критеріїв оцінки знань.
- •Математики . Дніїфонефотт.К д.Дл у, 2011. 24 і
- •Монотонність:
- •Графік функції (р, оберненої до /, симетричний графіку / відносно прямої
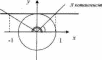
- •Тригонометричні функції
- •Перетворення графіків
Перетворення графіків
y = f(x) + b- паралельне перенесення вздовж вісі Оу функції у = /(х)
b > 0 _уТ;6<0 4.
y = f(x-a)- паралельне перенесення вздовж вісі Ох функції у = f(x): а>0х—>;а<0х<-.
у - к ■ f(x) - стягнення (поширення) вздовж вісі Оу функції у = /(х)
ft и
\к\>\ - v|^, ,к\<\ - уЧ-
y = f(k-x) - стягнення (поширення) вздовж вісі Ох функції у = /(х)
к\> \ — х —¥ ^3 I k ] < 1 — х < ^ .
.У = - fix)- симетрія відносно вісі Ох функції у = /(х).
>’ =! fix) \ -симетрія відносно вісі Ох від’ємних значень функції у = /(х). v = /! х j - симетрія відносно вісі Оу функції у = /(х).

D = Ь2 - 4ас - дискримінант:
якщо D=0 — корені дійсні і рівні
-со < а < +00
К
■ 1-як, к є Z
4
/gx = 0, х = лк, к є Z ж
tax = 1, х =—(- лк, keZ 4
х = arctga + лк, к є Z
arctg(-a) = -arctga гострий, від’ємний кут
якщо D<0 дійсних коренів не має
2а
якщо D>0 — корені дійсні і різні
п.
?х = й,
2а
- 4 ас
Квадратне рівняння має вигляд ах2+Ьх + с = 0 хі,2
у = ах' +Ьх + с квадратична функція, графіком є парабола.
Ь
Вершина: хе у„ =у(хв); якщо а > 0 —» и;якщо а< 0
-
c»gx = а,
оо < а < +00
Якшо коефіцієнт Ь парний Ь=2к, то корені визначаються х
2 [х1+х2=-р,
Якщо а = 1, то рівняння - зведене X + рх + ^ = 0 і _
[ Х] ' Х2 — Ч-
ах2 + Ьх + с = а - (х - х,) • (х - х2)
ctgx = 0, х = —і- лк, к є Z 2
c/gx = 1, х = — + лк, к є Z 4
л
ас
tgx -
arcctg (-а) = л - arcctg а тупий, додатній кут х = -— + як, к є Z
х = arcctg а + лк, к є Z
Похідною функції у = fix) в точці х називається границя відношення приросту функції А у в цій точці до приросту аргументу Ах, коли приріст аргументу прямує до нуля
f'(х)= lim
лх^о Ах'
Ах = х-х0, х = х0+Ах, Ау = у(х0+Ах)-у(х0).
Основні правила диференціювання функції
(С и)'= С-и'; 2. (u ± v)' = u' ± v';
„ ( \Г І , г ( U Л U - V-U-V
З. (и ■ V) = U ■ V + U ■ V ; 4. - = -
V / V2
(/(«(v (*))))' = /„'• «v • v' - похідна складної функції f(x) = (f(u(v(x))));
,/ч_и'(0 . , ... ,/ ч f X = v(t),
J \Х>~~ТГ: - похідна функції, яка задана параметрично 7w=i
v(0 ff- Ь = u{l).
Таблиця похідних елементарних функцій
1. (ха)' = а-ха-\ х' = \, (Vx)' =
2-Vx ’
(a* )' = ax Ina, (ex)' = ex.
(logax)' = —|— (7«x/ = -, x-lna x 4. (sin x/ = cosx, (cos x)' = - sinx,
0& *)' = (c/£x)' =—7~y
COS X sin X
(arcsin x)' = i=r (arccos x/ =
л
- X
_L
1 + x2 ’
.2
/ї - x2 Vl(arctg x)' -——- (arcctg x)' = -
Характерні точки та проміжки функції
Точка х„ називається критичною точкою І роду функції у = fix), якщо
! у'(х0) = о.
Диференційована функція у = f(x) зростає на проміжку х є (а, Ь) тоді і тільки тоді, коли перша похідна додатна: у Т <Ь у'(х)> 0 ,
Диференційована функція у - f(x) спадає на проміжку х є (а, Ь) тоді і тільки тоді, коли перша похідна від'ємна: /4- О у'(х)<0.
Точка х0 називається точкою максимуму функції у = fix), якщо існує такий окіл точки Х0, для всіх точок х якого виконується нерівність /(х)</(х0). Якщо похідна при переході через критичну точку змінює знак з "+" на :
Утах(х0) о у'(х):
Точка х0 називається точкою мінімуму функції у = /(х), якщо існує такий окіл точки щ, для всіх точок х якого виконується нерівність f (х) > /(х0) , Якщо похідна при переході через критичну точку змінює знак з на "+": ушіп(х0) <=>
Точки мінімуму та максимуму називаються точками екстремуму.
Точка х0 називається критичною точкоюIIроду функції у = /(х),якщо
у"{ж0) = 0.
Диференційована функція y = f (х) , х є (а, Ь) називається опуклою на проміжку, якщо всі її точки (крім точки дотику) лежать нижче довільної її дотичної, друга похідна від'ємна: у Г) О у”(х)<0.
Диференційована функція y = f(x) , хє(а,Ь) називається угнутою на проміжку, якщо всі її' точки (крім точки дотику) лежать вище довільної її дотичної, друга похідна додатна: y^J о у"(х)> 0.
Точка графіку функції y = f(x) називається точкою перегину. якщо вона відділяє її опуклу частину від угнутої. Друга похідна при переході через критичну точку змінює знак з "+" на або з на "+":
Г f ^tt f і
У перегину
Загальна схема дослідження функції:
Знайти область визначення функції.
Знайти точки перетину з осями координат.
Дослідити функцію на неперервність. Знайти точки розриву та односторонні границі в цих точках. j
Знайти асимптоти графіка функції.
З'ясувати, чи буде функція парною, непарною, періодичною.
Знайти критичні точки І роду.
Знайти проміжки монотонності та екстремуми функції.
Знайти критичні точки II роду.
Знайти проміжки опуклості та точки перегину функції.
Побудувати графік функції.
Геометричний зміст похідної: f'(x0)-k, k = tga.
Похідна функції y-f(x) в фіксованій точці ха дорівнює кутовому коефіцієнту дотичної, яка проведена до графіка цієї функції в його точці з абсцисою х0 під кутом а (кут між дотичною та віссю Ох).
Рівняння дотичної: У ~ У0 — У '0( х — Х0 ) .
_ )
Рівняння нормалі: У У о — , ( х хоУ.
-Уо
Фізичний зміст похідної:
Миттєва швидкість ? (%) прямолінійного руху матеріальної точки в будь-який момент часу є похідна від шляху S по часу t: S'(t0) = v.
Прискорення a (ta)e друга похідна від шляху S по часу t: S"(t0) - v'(t0)= а .
сі А
Сила F(x) є похідна роботи А по переміщенню х: ^(х) = -j—.
d А
Потужність N(t) є похідна роботи А по часу t: ^ =
aq
Сила струму 1(1.) є похідна заряду q по часу 1 \ ■'(! )- —jj.
Лінійна щільність р(1) є похідна маси т тонкого стержню по його довжині /:
d т
Функція Fix) називається первісною функції/(х) на проміжку іа\Ь). якщо F(х) диференційована на (а; Ь) і вірна рівність F'(x) = fix), xe(a;b).
Невизначеним інтегралом функції/(х) наз. сукупність усіх первісних
J/(x) dx = F(x) + С.
Визначений інтеграл функції fix) на проміжку (а; Ь) - відповідний приріст її первісної (формула Ньютона-Лейбниця )
b
J
= F(b)-F(a)
а
f(x) dx = F(x)a
Основні властивості інтегралів
(jf(x)dx) = f(x) 5. d (j /їхJ dx) = f (x) dx
\d F(x) = F{x) + C 6. \ f(kx + b)dx = —-F(kx + b)+N
k
jc ■ f(x) dx = C ■ J/'(.v) dx 7. \{f(x) ± g (xj) dx = \f (x) dx±\g(x) dx
b a b c b
jf(x)dx = - jf(x)dx g. jf(x)dx=jf(x)dx+jf(x)dx
a b a a c
Таблиця основних невизначених інтегралів
\xadx-^~- + C ■ [dx = x+ C 8' \tgxdx = -\n\cosx\+C J a +1 ’ J
a 9. \ctgxdx = \n\smx\+C
J— = In | .v | +C
x c dx , . x . „
J = In1 tg t-C
Стала функція, 9
а< 0, a = 2n + l, nsN. 9
Обернені тригонометричні функції 13
Перетворення графіків 15
ft и 15
л/ї - x2 Vl 20
l + t , 1 + ^ і+^2- 1 + Ґ 20
а І, 21
fcosxcfe = sinx + C 12. f :-arcsin—+ C
J 4a —x a
f—= fgx + C 1Л r 1 , x cos x 13. I— I = ~arctg~ + C
J a + x a a
f-^- = -cfgx + C , , f dx 1 1я, ^ -а і , /-> jsm'x 14. H j- =* —— In | !+C
Jx -a 2a x + a
Основні методи інтегрування:
безпосереднього інтегрування: після алгебраїчних перетворень підінтегральної функції та застосування властивостей інтегралів, звести даний інтеграл до табличних інтегралів;
\/(Х> & = 1= і/(т)
заміни змінної:
інтегрування частинами: виконати заміну функцій таким чином, що за змінну и беремо функцію, яка при диференціюванні змінює свою природу
(наприклад: и = 1пх, сій = —; и = агс^ х, <іи = -Х - )
X 1 + х'
Ґ Р(х) ,
раціональних дробів: і ~~ ВИДШИТИ Ц,ЛУ частину; розкласти
знаменник 0(х) на простіші множники; розкласти правильний раціональний дріб на простіші дробі (знайти невизначені коефіцієнти); знайти кожен новий інтеграл (за допомогою попередніх методів);
інтегрування тригонометричних функцій |/?(5Іпх.собх)сіх ; після перетворень тригонометричних функцій (див. с.12) до табличних інтегралів;
х
за допомогою універсальної підстановки tg— = t; х = 2 аг^ І;
dt . 2^2 2/ \~~tg2 “ і_?2 йх~ С05х — -
->5 ОШ Л — — О Л- — —
l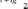 + t
,
1 + ^ і+^2-
1
+
Ґ
+ t
,
1 + ^ і+^2-
1
+
Ґ
Застосування визначеного інтеграла Геометричні задачі
ь
Площа плоскої фігури : в прямокутних координатах;
S = — JP (<p)d(p - в полярних, S = т ]v(t)(p(t)dt -в параметричній формі.
2
и ч
Ь
Довжина дуги кривої. І = |V*+ (f(x)Y dx •
і = +(р'(<р)): л<р\ і= І^х'У +(у')2 аі,
а І,
Площа поверхні обертання 5 = 2,т [>\/1 +(у')~ сі х
5[=2п\у-\(х')2 +(у')2 сіі; 5= Ур2 + (р'(ср))2 сі(р_
а
Ь
Об’єм тіла обертання з відомим поперечним січенням ^ х) ^х ■
ь
і Ох Ух = л\у2(х)сіх.
ВЗДОВЖ ВІСІ
а
сі
ВЗДОВЖ ВІСІ Оу УV ~ Я $Х (У~)^у.
с
Фізичні задачі
Шлях, що проходе точка за проміжок часу [/,,72] , якщо швидкість
12
визначається формулою V =/(і): & — }/(О ^ І.
Статичні моменти Мх — \у сіЬ ^ Му = сі І ) де сі Ь = у]\ + (у )" сіх.
Стала функція, 9
а< 0, a = 2n + l, nsN. 9
Обернені тригонометричні функції 13
Перетворення графіків 15
ft и 15
л/ї - x2 Vl 20
l + t , 1 + ^ і+^2- 1 + Ґ 20
а І, 21
= ^\Х<І5 = ^\ХУ(ІХ, У = -^\усіб=-^\у1(ІХ, сіБ - у сіх.
Робота змінної сили А = \/(х)<Ьс,

Наближене обчислення визначеного інтеграла:
Ь-а
ф
Л +/з +- + ^ і
У 2 2 и
ормула прямокутників |/(х)с&:
ф
Ь ~ а ( /о + /„
_[/(*) <& *
ормула трапецій формула Сімпсона
/о + /„
Ь-а
]/(*)<& >
+ /і +/г +---+Л-1 +2
Зп
/і + /з +•••+/ і
4 2 2 2 УУ
Література
і '
Выгодский М.Я. Справочник по высшей математике. - М.: Наука,
1968.-784 с.
Выгодский М.Я. Справочник по элементарной математике. - М.: Наука, 1975.-416 с.
Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математике. -М.: Наука, 1986.-576 с.
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, 2 ч. — М.: Высшая школа, 1986. — 304 с.
Сборник задач по математике (для поступающих в ВУЗы). Сканави М.И. - К.: Каннон, 1997,- 527 с.
