Графіки тригонометричних функцій

Графіком функції е синусоїда, яка обмежена прямими у ——І, у —І.

х

У

т

	0°	30° (-) 6	45° (-) 4	60° (-) 3	90° (-) 2
sin	0	1/2	■42/2	V3/2	1
COS	1	уіЗ/2	V2/2	1/2	0
lg	0	V3/3	1	V3	-
ctg	-	V3	1	V3/3	0

змінюється;

cos (- а) = cos а sin(-a) = - sin а tg(-a)=-tga ctg(- а) = -ctg а

Періодичність

cos(2tt + а) - cos а sin(2;r + a) = stn а tg{n + а) = tg а ctg(iz + а) = ctg а

Знаки залежать від чверті (х: у)

Формули зведення:

S визначити чверть;

'S - II - знак функції;

S - II - назву нової функції за умови, що

Тригонометричні функції

'

Тригонометричні Функції

не змінюється.

cos а sin а

Парність

cos а =

а

Зв’язок між градусною та радіанною мірою кута: я (рад) = 180°

cos a sina 1

sina cos a

sin² a + cos² a - 1 ; tg a = -

ctg a - -

X

■-

<u

“ I

° 1 U CÏ

O ‘m .0 *c u

1|

a

tg a -ctg a = 1 ; cosec a -

sec a - -

cos a 1

1 + tg²a = sec² a = -

1H- c^“# = cosec a ■

sm~ 1 -tga-tgP

cos a

sin(a + 0) = ш or cos p + cos a sin p ; s//?(ar - p) - sina cos p - cos a sin p; cos (a + P) = cos a cos P - sina sin Pi cos(a - p) = cos a cos P + sina sin p ;

Il

> fU

S cû

Q. Ю

O cl

^e §

tga-tg p l + tga-tg p

tg{a~P)--

1 - cos а

■ ^а + sin— = ± 2

а

cos— = ±. 2

x sin 2a = 2 sin a ■ cos a ;

m P- *=t I

O cu ~ 2 -2

c z cos 2a = cos a - sw ^ a

I" „ 2fga

a. te 2a = —;

о 1 -t_g'_a

ctg²a -1 2 ctga

Зв'язок між половинним та подвійним аргументу

о

І*

0. і

§ І

0. & і ^a

■£.

CL

О

Є

1 + cos а

1 - cos а

а

te— = ± .

‘2 'У 1 +

cos а

a sin а 1 - cos а

^,8- = - = —:

2 1 + cos a sin а

ctg 2а ■

а

а

2 tg

1 -tg'

cos а =

sin а = -

а

а

1. +

   1 +tg

   tg^l-

p

II

5. и

Cl cQ ° ^ е 5

су t

5. Я

= ^ [««(or + //)+іїш(а - /?)]; p = “[cos(a + /?)+ cos(a - /?)];

sina-cos

cos а • cay

sina ■ sin p = —[cos (a - p)-cos (a + /?)].

ia + P),

sin

tga + tg p =

cos a ■ cos P

sin(a — P) cos a cos p

2

a + p 2 ’ a-p

X >,

S o

O cf

CD ⁴

I- m

11 _

CL ^

0) S

■= &

tga - tgP =

2

a-p

n ^ a + p

cos a + cos b = 2 cos cos

2

. . a + p . cos a - cos p = -2sm sin

. „ _ . ar + p a-p sma + sinP ~ 2sin — • cos-

■ n

-, ■ ^a - P

sma - sinp = 2sin cos

у

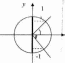
Обернені тригонометричні функції

Обеунені тригонометричні фунти

■ у = arcsin х (-1 < х < і); ¹ у - arccos х

( 1 < л < І і:

у

у = arctg х (— °о < х < +со

гострий від ’ємний кут.

= arcctg х (— оо < X < +со ).

агсctg (- а) = к - arcctg а, arccos (- а) = п - arccos а тупий додатній кут;

s

СК

X

X

X І m 5

° І (J СІ

О 'со ш 'с

и

П _л 7T

— _s arctgx + arcctgx - —_;

іпл/l -x² =

arccosx = arcsin-

in (arcsina) = а, cos (arccos аг) = tg (arctgx ) = х, ctg(arcctgx) =

a

1 . x

arctgx = arcctg— = arcsin —j= x VI

1

arcctgx- arctg- = arcsin

rcsin x + arccosx arcsin x = arccos Vl - x² = arctg

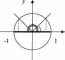
Розв’язування тригонометричних рівнянь

sinx = a, -1<я<1

х = (-1) arcsina+лк, keZ

arcsin(-a) = - arcsin а гострий, від’ємний кут

я і

sinx = -1, х = <г2лк, keZ

2

sinx = 0, х = лк, к є Z її

sinx - І, х = — + 2 лк, keZ

2

cosx = а, -1 < а < \ х = ±arccosa + 2лк, к є Z

arccos (-а) = ж — arccos а тупий, додатній кут

cosx = -1, х = -ж + 2 лк, keZ л

cos х = 0. cosx = 1, х = 2лк, к є Z