
- •Как вычисляются основные числовые характеристики по результатам выборки: «группа средних». Объяснить на примерах.
- •1.3 Средние величины: средняя, средневзвешенная, мода Мо, медиана Ме. Показатели вариации: дисперсия, среднее квадратическое отклонение, коэффициент вариации.
- •14. Приведите примеры зависимых и независимых событий
- •16. Дайте возможные определения вероятности. Приведите примеры их использования.
- •17. Что такое относительная частота события, как она связана с вероятностью?
- •18. Что такое случайная величина (св)? Какие виды св известны?
- •26. В каких случаях применяют формулу Байеса? (Показать на примерах)
- •27. В каких случаях применяют формулу Бернулли? (Показать на примерах)
- •§ 1. Испытания Бернулли.
- •§ 2. Наивероятнейшее число успехов.
- •Если число np-q - дробное, то существует одно наивероятнейшее число m*;
- •Если число np-q - целое, то существует два наивероятнейших числа
- •28. В каких случаях применяют формулу Пуассона? (Показать на примерах)
- •29. Что такое функция распределения св? Что такое плотность вероятности св? Приведите ее свойства.
- •30. Как рассчитывается вероятность попадания св в определенный интервал с помощью функции распределения, с помощью плотности вероятности?
- •36 Что такое дерево вероятностей? Сформулируйте правила построения и проверки корректности дерева вероятностей?
- •37. Какая выборка называется репрезентативной? Каким образом можно извлечь репрезентативную выборку?
- •38. Какой интервал мы называем доверительным?
- •39 Что называется уровнем доверительности (confidence level)?
- •40. Какой из двух доверительных интервалов больше: двусторонний 99% или двусторонний 95%? Объясните.
38. Какой интервал мы называем доверительным?
Доверительный интервал - это допустимое отклонение наблюдаемых значений от истинных. Размер этого допущения определяется исследователем с учетом требований к точности информации. Если увеличивается допустимая ошибка, размер выборки уменьшается, даже если уровень доверительной вероятности останется равным 95%.
Доверительный интервал показывает, в каком диапазоне расположатся результаты выборочных наблюдений (опросов). Если мы проведем 100 одинаковых опросов в одинаковых выборках из единой генеральной совокупности (например, 100 выборок по 1000 человек в каждой в городе с населением 5 миллионов человек), то при 95%-й доверительной вероятности, 95 из 100 результатов попадут в пределы доверительного интервала (например, от 28% до 32% при истинном значении 30%).
Например, истинное количество курящих жителей города составляет 30%. Если мы 100 раз подряд выберем по 1000 человек и в этих выборках зададим вопрос "курите ли Вы?", в 95 из этих 100 выборок при 2%-м доверительном интервале значение составит от 28% до 32%.
39 Что называется уровнем доверительности (confidence level)?
Доверительный уровень отражает количество данных, необходимых оценщику для того, чтобы утверждать, что обследуемая программа имеет должный эффект. В общественных науках традиционно используется 95% доверительный уровень. Однако для большинства общественных программ уровень в 95% является излишним. Доверительный уровень в интервале 80-90% является достаточным для адекватной оценки программы. Таким образом, можно уменьшить размер репрезентативной группы, тем самым уменьшив и затраты на проведение оценки.
В процессе статистической оценки проверяется нулевая гипотеза, которая состоит в том, что программа не имела должного эффекта. Если полученные результаты значительно отличаются от изначальных предположений о правильности нулевой гипотезы, то последняя отклоняется.
40. Какой из двух доверительных интервалов больше: двусторонний 99% или двусторонний 95%? Объясните.
Двусторонний доверительный интервал 99% больше, чем 95%, так как в него попадает больше значений. Док-во:
С помощью z-значений можно точнее оценить доверительный интервал и определить общую форму доверительного интервала. Точная формулировка доверительного интервала для выборочного среднего имеет следующий вид:
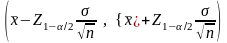 .
.
Таким образом, для случайной выборки
25 наблюдений, удовлетворяющих нормальному
распределению, с
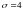 доверительный интервал выборочного
среднего имеет следующий вид:
доверительный интервал выборочного
среднего имеет следующий вид:
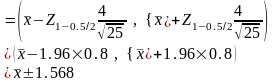
Т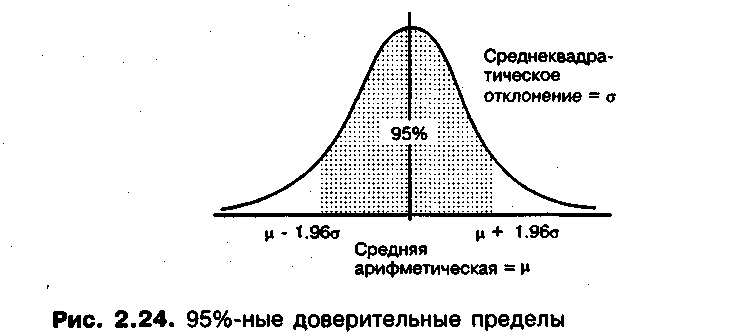 аким
образом, на 95% можно быть уверенным, что
значение
аким
образом, на 95% можно быть уверенным, что
значение
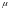 лежит в пределах ±1,568 единицы от
выборочного среднего. С помощью такого
же метода можно определить, что 99%-ный
доверительный интервал лежит в пределах
±2,0608 единицы от выборочного среднего
лежит в пределах ±1,568 единицы от
выборочного среднего. С помощью такого
же метода можно определить, что 99%-ный
доверительный интервал лежит в пределах
±2,0608 единицы от выборочного среднего
значение
![]() Таким
образом, имеем
Таким
образом, имеем
![]()
![]() и отсюда
и отсюда
![]() ,
Аналогично получаем нижний предел,
который равен
,
Аналогично получаем нижний предел,
который равен
![]()
