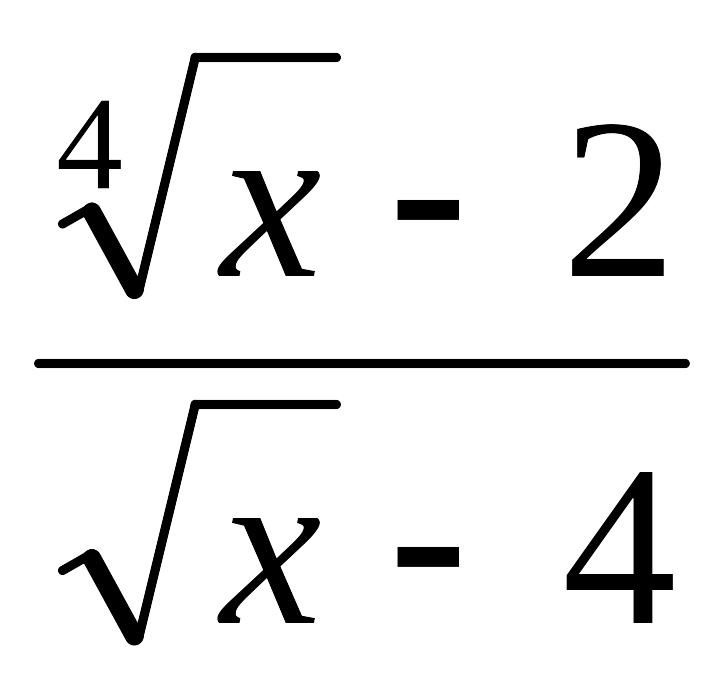- •1 Пользуясь критерием Коши, доказать сходимость или расходимость последовательности :
- •2 Пользуясь теоремой о существовании предела монотонной и ограниченной последовательности, доказать сходимость последовательности :
- •3 Вычислить :
- •4 Вычислить :
- •5 Для последовательности найти и :
- •Решение типовых примеров
- •2.20 Пользуясь теоремой о существовании предела монотонной и ограниченной последовательности, доказать сходимость последовательности
- •2 Пользуясь определением предела по Коши (на «языке »), доказать, что .
- •3 Используя определение предела функции по Гейне (на языке последовательностей), доказать, что не существует предела .
- •4 Используя логические символы (на языке « ») сформулировать утверждение и привести соответствующие примеры.
- •5 Найти односторонние пределы или показать, что эти пределы не существуют. Если существует , найти его.
- •6 Пользуясь определение предела по Коши, доказать, что число не является .
- •Решение типовых примеров
- •2 Используя свойства пределов и первый замечательный предел, вычислить :
- •3 Используя свойства пределов, второй замечательный предел и равенства , , вычислить :
- •4 Используя свойства пределов, известные пределы, предел , вычислить :
- •1 Определить порядок относительно бесконечно малой при (при ) функций :
- •2 Для бесконечно малых при (при ) функций и выяснить, какие из следующих соотношений верны: 1) , 2) , 3) , 4) , 5) , 6) :
- •3 Для бесконечно малой при (при ) функции найти бесконечно малую при функцию вида ( ) такую что: 1) , 2) при :
- •4 Вычислить , используя принцип эквивалентности бесконечно малых:
- •Решение типовых примеров
Решение типовых примеров
1.20. Для
функции
 ,
,
![]() ,
,
![]() ,
,
![]() и
и
![]() ,
,
![]() найти
,
чтобы для любых
,
удовлетворяющих условию 0<
<
,
выполнялось неравенство
<
.
найти
,
чтобы для любых
,
удовлетворяющих условию 0<
<
,
выполнялось неравенство
<
.
Решение. Так как , , , , то
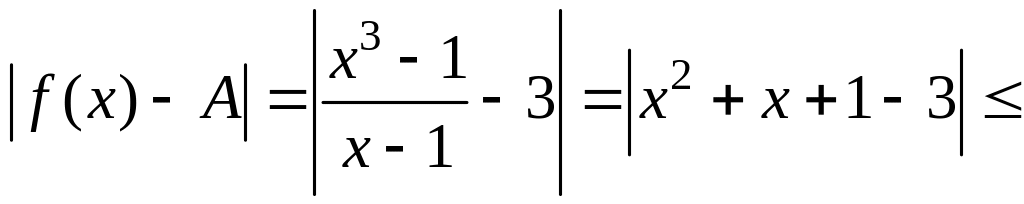
![]() .
.
Будем искать нужное
среди
![]() .
Для
,
удовлетворяющих неравенству
.
Для
,
удовлетворяющих неравенству
![]() ,
имеем
,
имеем
![]() и
и
![]() .
Поэтому
.
Поэтому
![]() .
.
Теперь если
![]() ,
то для него
найдем из равенства
,
то для него
найдем из равенства
![]() ,
т.е.
,
т.е.
![]() .
Если же
.
Если же
![]() ,
то полагаем
,
то полагаем
![]() ,
т.е.
,
т.е.
![]() .
Заметим, что найденные
.
Заметим, что найденные
![]() .
.
2.20. Пользуясь определением предела по Коши (на «языке »), доказать, что .
Решение.
Так как
![]() ,
,
![]() ,
,
,
,
![]() ,
то
,
то
![]() .
.
Возьмем
и будем искать нужное
среди
.
Тогда
![]()
![]() .
Поэтому
.
Поэтому
![]() и
и
![]() .
.
Тогда, если
![]() ,
то
,
то
![]() для всех
для всех
![]() и
и
![]() .
Поэтому, положив
.
Поэтому, положив
 ,
будем иметь, что
при
для
,
будем иметь, что
при
для
![]() и
справедливо неравенство
и
справедливо неравенство
![]() .
.
Итак, показано,
что
![]() .
.
3.18.
Используя определение предела функции
по Гейне (на языке последовательностей),
доказать, что не существует предела
,
если
![]() ,
.
,
.
Решение. Для последовательности
![]() ,
,
![]() .
.
С другой стороны,
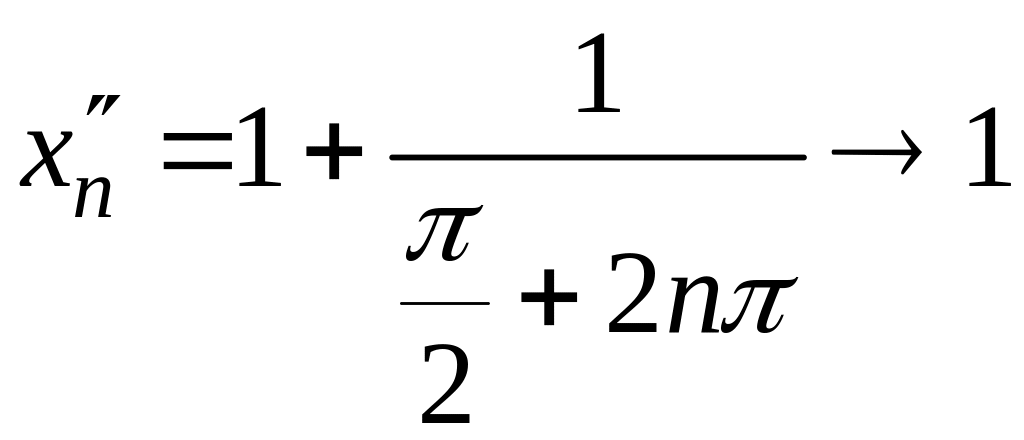 ,
а
,
а
![]() .
.
Из определения
предела по Гейне следует, что предел
![]() не существует.
не существует.
4.20.
Используя логические символы
(на языке «
»)
сформулировать утверждение
и привести
соответствующие примеры, если
![]() ,
,
![]() .
.
Решение.
На языке
«
»
![]()
![]()
![]()
![]() такое, что
такое, что
![]() .
.
Пример:
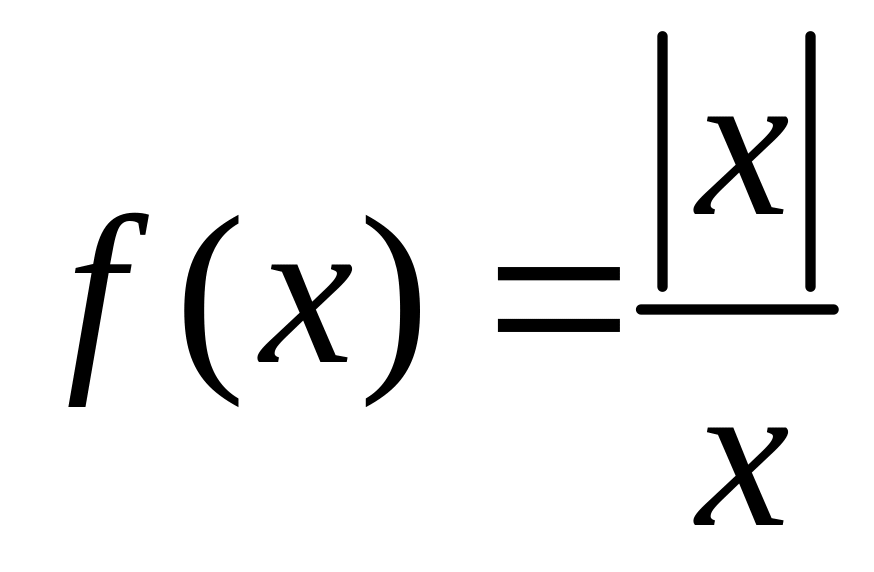 ,
,
![]() ,
,
![]()
 .
.
5.18.
Найти односторонние пределы
,
где
 ,
,
![]() ,
или показать, что эти пределы не
существуют. Если существует
,
найти его.
,
или показать, что эти пределы не
существуют. Если существует
,
найти его.
Решение.
Покажем,
что не существует
 .
Для доказательства воспользуемся
определением предела по Гейне: при
.
Для доказательства воспользуемся
определением предела по Гейне: при
![]()
 ,
,
![]() ;
;
![]() ,
,
![]() .
.
Итак, показано,
что не существует
.
Аналогично показывается, что не
существует
 .
Таким образом, показано, что не существует
.
Таким образом, показано, что не существует
 .
.
6.20
Пользуясь определение предела по Коши,
доказать, что число
не является
,
если
![]() ,
,
![]() ,
,
,
,
![]() .
.
Решение.
Нужно
показать, что
![]() такое, что
такое, что
![]()
![]() ,
удовлетворяющее условию
,
удовлетворяющее условию
![]() ,
для которого
,
для которого
![]() .
Возьмем
.
Возьмем
![]() .
Для любого
.
Для любого
![]() положим
положим
![]() .
Тогда
.
Тогда
![]()
![]() и
и
 .
.
Нужное утверждение доказано.
7.18
Найти
и
,
если
![]() ,
,
![]() ,
.
,
.
Решение.
Так как
![]() ,
то
,
то
![]() .
Поэтому если
– частичный предел
в точке
,
то
.
Поэтому если
– частичный предел
в точке
,
то
![]() .
С другой стороны, имеем: при
.
С другой стороны, имеем: при
![]() ,
а
,
а
![]() ;
;
,
а
![]() .
.
Следовательно,
![]() ,
а
,
а
![]() .
.
Лабораторная работа № 8
Замечательные пределы. Вычисление пределов.
Необходимые понятия и теоремы: первый и второй замечательные пределы, предел и арифметические операции, пределы монотонной функции, предел композиции, критерии Коши существования предела.
Литература: [1] с. 170 – 180; [2] с. 56 – 66; [6] с. 98 – 102, 128–137.
1 Используя свойства пределов и известные пределы, вычислить :
№ |
A |
B |
C |
|||
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1.1 |
0 |
|
4 |
|
0 |
|
1.2 |
1 |
|
16 |
|
1 |
|
1.3 |
+∞ |
|
8 |
|
|
|
1.4 |
|
|
2 |
|
0 |
|
1.5 |
1 |
|
1 |
|
0 |
|
1.6 |
2 |
|
1 |
|
1 |
|
1.7 |
1 |
|
0 |
|
0 |
|
1.8 |
3 |
|
|
|
1 |
|
1.9 |
1 |
|
1 |
|
|
|
1.10 |
|
|
1 |
|
+∞ |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1.11 |
|
|
|
|
+∞ |
|
1.12 |
1 |
|
1 |
|
1 |
|
1.13 |
0 |
|
0 |
|
+∞ |
|
1.14 |
1 |
|
1 |
|
+∞ |
|
1.15 |
1 |
|
16 |
|
+∞ |
|
1.16 |
|
|
1 |
|
+∞ |
|
1.17 |
|
|
4 |
|
+∞ |
|
1.18 |
1 |
|
1 |
|
|
|
1.19 |
|
|
1 |
|
|
|
1.20 |
1 |
|
1 |
|
1 |
|