7. Мкт. Основное уравнение кинетической теории газов. Газовые законы. Уравнение Менделеева-Клапейрона.

Основным уравнением кинетической теории газов называется соотношение, связывающее давление (величину, измеряемую на опыте) со скоростью или кинетической энергией молекулы идеального газа.

В молекулярно-кинетической теории пользуются идеализированной моделью идеального газа, согласно которой считают, что:

1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;

2) между молекулами газа отсутствуют силы взаимодействия;

3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.

Скорости частиц как по модулю, так и по направлению могут быть любыми, изменение их происходит непрерывно.

Рассмотрим одноатомный идеальный газ. Предположим, что молекулы газа движутся хаотически, число взаимных столкновений между молекулами очень мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенками сосуда абсолютно упругие. Выделим на стенке сосуда элементарную площадку s (cм. рис.). При каждом соударении, молекула, движущаяся перпендикулярно площадке, передает ей импульс т₀ v–(–m₀ v) = 2 т₀ v,

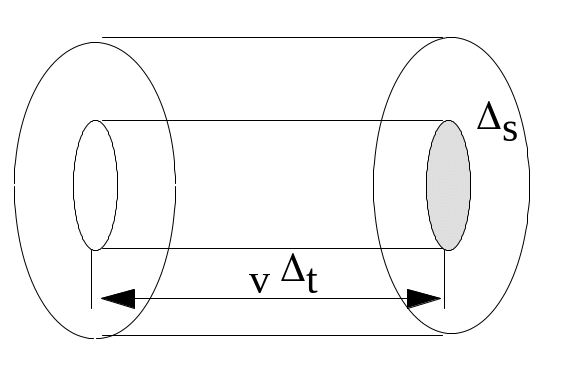
где т₀ — масса молекулы, v – ее скорость. За время t площадки s достигнут только те молекулы, которые заключены в объеме цилиндра с основанием s и высотой vt. Число этих молекул равно ns vt, где п – концентрация молекул. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлений, так что в любой момент времени вдоль каждого из них движется 1/3 молекул, причем половина из них (1/6) движется вдоль данного направления в одну сторону, половина – в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку s будет . При столкновении с площадкой эти молекулы передадут ей импульс: .

Тогда давление газа на стенку сосуда: (1)

Если газ в объеме V содержит N молекул, движущихся со скоростями v₁, v₂., то учитывают среднюю квадратичную скорость: (2), характеризующую всю совокупность молекул газа. Уравнение (1) с учетом (2) примет вид . (3)

Данное выражение называется основным уравнением молекулярно-кинетической теории идеальных газов. Оно устанавливает связь между давлением и среднеквадратичной скоростью.

Введем Е – среднюю кинетическую энергию хаотического поступательного движения одной молекулы, тогда основное уравнение запишется как: или Е.

Здесь давление связано со средней энергией поступательного движения молекул. При переходе к равновесию от одной части газа к другой передается энергия. Выравнивается не энергия всего газа как целого, а средняя кинетическая энергия, отнесенная к одной молекуле. Температура газа пропорциональна средней кинетической энергии его молекул: Т  Е. Средняя кинетическая энергия поступательного движения молекулы Е = , (4)

где k - постоянная Больцмана, : k=1,38.10^-23 Дж/К, Т – температура, выраженная в кельвинах. Из формулы (4) следует, что абсолютная температура является мерой средней кинетической энергии поступательного хаотического движения молекул. Подставляя в (3) это выражение, получим, что давление идеального газа связано с температурой соотношением:

.

Давление определяется только концентрацией (при постоянной температуре) и не зависит от сорта молекул.

Газовые законы устанавливают связь между двумя параметрами состояния при постоянном третьем параметре для данной массы газа.

Экспериментальное исследование свойств газов, проведенное в ХVII-XVIII вв. Бойлем, Мариоттом, Гей-Люссаком, Шарлем, привело к формулировке газовых законов (с учетом представления абсолютной температуры)

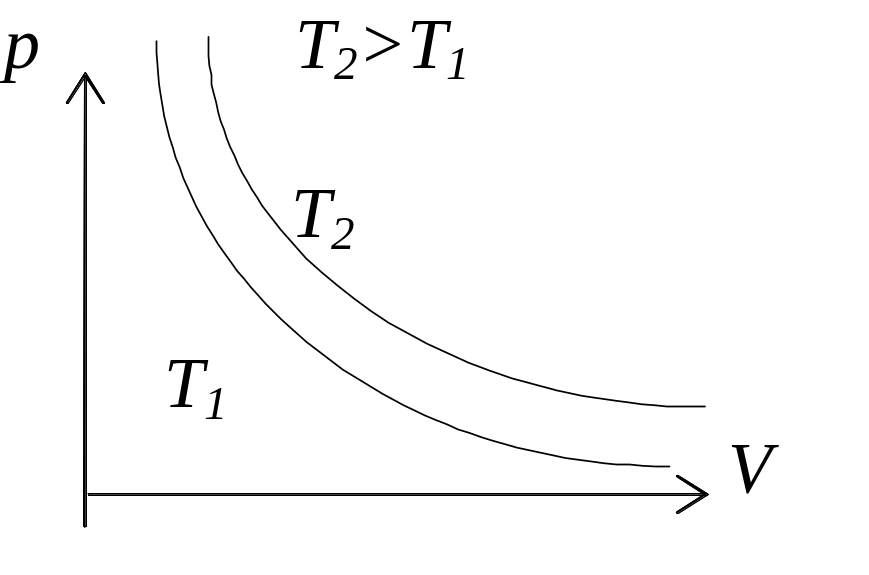
1. Изотермический процесс. pV=const – уравнение изотермы.

Чем выше изотерма, тем более высокой температуре она соответствует, T₂>T₁.

2. Изобарный процесс. – уравнение изобары. Чем ниже к оси температуры наклонена изобара, тем большему давлению она соответствует, р₂ > p₁.

3. Изохорический процесс. – уравнение изохоры. График зависимости р от Т изображен на рис 7.3. Чем ниже к оси температуры наклонена изохора, тем большему объему она соответствует, V₂ > V₁.

Комбинируя выражения газовых законов, получим уравнение, связывающее р, V, Т (объединенный газовый закон): .

Постоянная в этом уравнении определяется экспериментально. Для количества вещества 1 моль газа она оказалась равной R=8,31 и была названа универсальной газовой постоянной.

1 моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде-12 массой 0,012 кг. Число молекул (структурных единиц) в 1 моле равно числу Авогадро: N_A=6,02.10²³моль^-1. Для R справедливо соотношение: R=k N_A. Итак, для одного моля: . Для произвольного количества газа =m/( - молярная масса газа.): ,

уравнение Менделеева-Клапейрона.