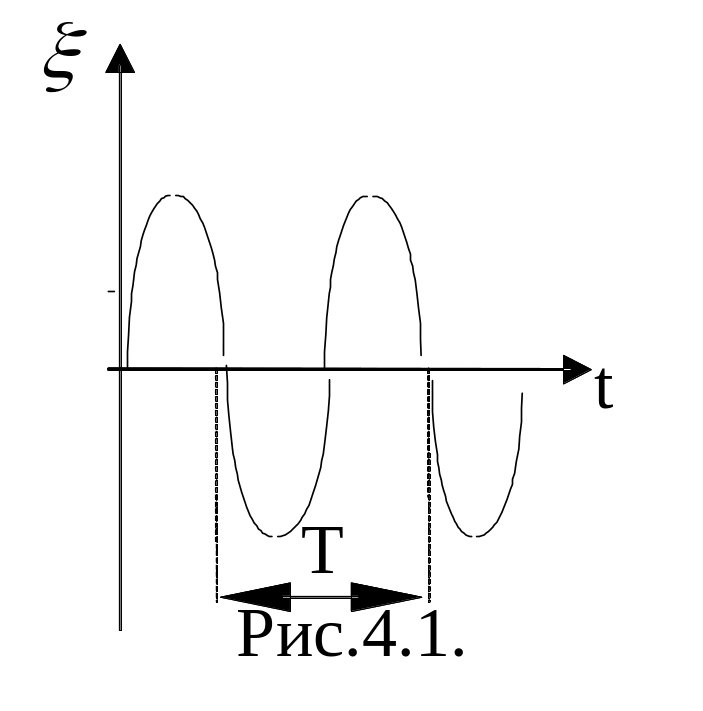
5. Механические колебания. Свободные, затухающие и вынужденные колебания линейного осциллятора.

Движения, обладающие той или иной степенью повторяемости, называются колебаниями. Если колебания повторяются через равные промежутки времени, то они называются периодическими. В зависимости от физической природы колебательного процесса и «механизма» его возбуждения различают механические и электромагнитные колебания. Гармонические – это такие колебания, которые описываются периодическим законом или (1)

где – периодически изменяющаяся величина (смещение, скорость, сила и т.д.). Система, закон движения которой имеет вид (1), называется одномерным (линейным) классическим гармоническим осциллятором или сокращенно гармоническим осциллятором.

Амплитуда А, определяющая размах колебаний, равна абсолютному значению наибольшего отклонения от значения в состоянии равновесия. Аргумент синуса или косинуса называется фазой колебания, – начальная фаза. –частота колебаний, численно равная числу колебаний, совершаемых за единицу времени. Частота, при которой за 1с совершается одно полное колебание, называется герцем (Гц).Т – период – время, за которое совершается одно полное колебание.

Система, совершающая колебания, называется маятником.

Пружинный маятник имеет период , где m – масса тела, закрепленного на пружине жесткостью k. .Математический маятник – это модель, в которой вся масса сосредоточена в материальной точке, колеблющейся на невесомой и недеформируемой нити длиной . Период колебаний : . Физический маятник – образует твердое тело, подвешенное в поле тяжести на закрепленной горизонтальной оси. Период колебаний физического маятника: , где J – момент инерции маятника относительно оси, m – масса тела, – расстояние от оси до центра тяжести тела.

Свободными (собственными) называются колебания, которые происходят в отсутствие переменных внешних воздействий на колебательную систему. Они возникают вследствие какого-либо начального отклонения этой системы от состояния ее устойчивого равновесия.

Рассмотрим смещение x колеблющегося тела относительно положения равновесия, то есть . Начало отсчета времени выберем так, чтобы =0. Уравнение гармонического колебания: , причем А и  – величины постоянные.

Первая производная от по времени дает выражение для скорости движения тела: ; (2)

Уравнения (2) показывают, что скорость, как и смещение, изменяются по гармоническому закону с той же частотой , но ее фаза отличается от фазы смещения на /2, то есть когда =0, то .

Ускорение изменяется со временем также по гармоническому закону:

, (3)

где – максимальное значение ускорения. Фаза ускорения отличается от фазы смещения на , а от скорости на /2. Из (3) следует. что значение ускорения в процессе колебательного движения равно:

. (4)

Таким образом, при гармоническом колебательном движении ускорение тела прямо пропорционально смещению от положения равновесия и имеет противоположный ему знак. Уравнение (4) можно переписать в виде: (5)

Это и есть дифференциальное уравнение гармонических колебаний. Если изменяется со временем согласно формуле (1), то оно удовлетворяет дифференциальному уравнению (5). Верно и обратное утверждение.

Реально свободные колебания под действием сил сопротивления всегда затухают. Пусть точка совершает линейное гармоническое колебание в вязкой среде. При малых скоростях: , где r – постоянная величина, называемая коэффициентом сопротивления среды. Уравнение колебаний: . Введем обозначения: , тогда дифференциальное уравнение затухающего колебания: (6)

где – коэффициент затухания, ₀ – собственная частота колебания. При отсутствии трения =0, уравнение примет вид уравнения для свободных незатухающих колебаний. В результате решения уравнения (6) получим зависимость смещения х от времени, то есть уравнение затухающего колебательного движения:

(7)

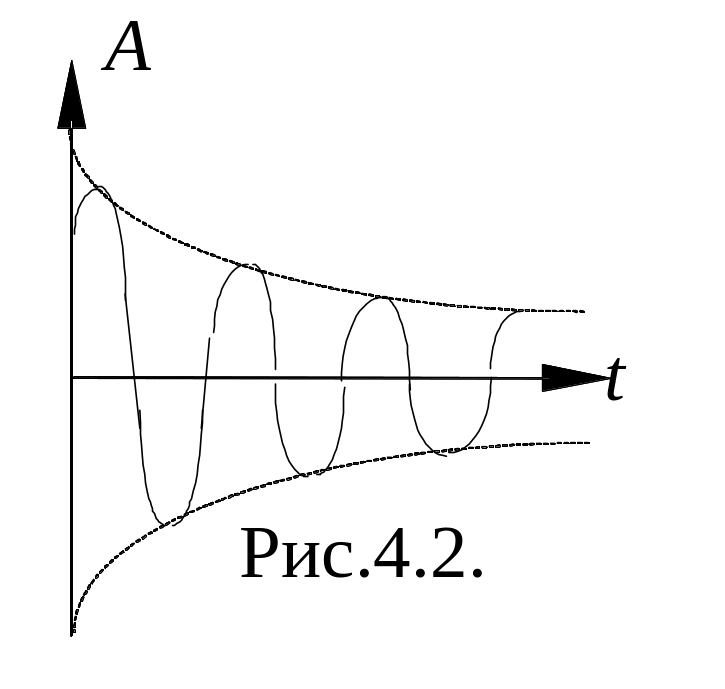
Выражение называется амплитудой затухающего колебания. Амплитуда уменьшается с течением времени и тем быстрее, чем больше коэффициент затухания. Огибающая на графике зависит от . Чем она больше, тем круче огибающая, то есть колебания быстрее затухают.

Путем подстановки функции (2) и ее производных по времени в уравнение (1), можно найти значение угловой частоты: . Период затухающих колебаний равен: .

Наглядной характеристикой затухания является отношение значений двух амплитуд, соответствующих промежутку времени в один период. Это отношение называют декрементом затухания : Его логарифм есть безразмерная величина, называемая логарифмическим декрементом затухания:

Колебания системы, которые совершаются за счет работы периодически меняющейся внешней силы, называются вынужденными.

Пусть на систему действует внешняя сила, меняющаяся со временем по гармоническому закону: , где F₀ – амплитуда силы (максимальное значение),  – угловая частота колебаний вынуждающей силы. Тогда уравнение движения будет иметь вид:

=

С учетом введенных в предыдущем случае обозначений получим дифференциальное уравнение вынужденного колебания:

= (8)

Решение дифференциального уравнения при установившемся движении имеет вид: (9)

где А,  – величины, которые требуется определить,  – круговая частота колебаний внешней переменной силы. Подставляя (9) в (8) (без вывода), получаем искомые величины:

;

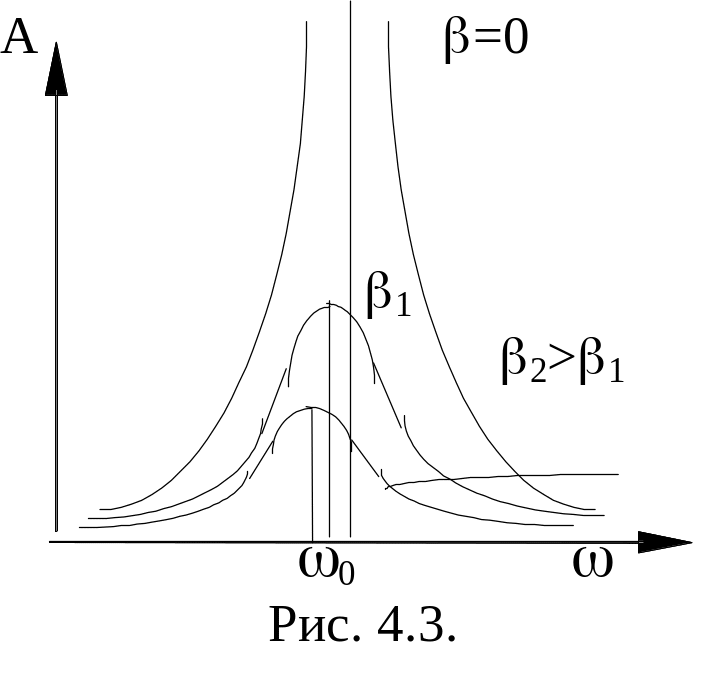
При некоторой частоте внешних сил знаменатель в выражении для А будет иметь минимальное значение, а амплитуда вынужденных колебаний – максимальное значение. Эта частота называется резонансной. Для ее нахождения, приравниваем к нулю производную: ,

откуда следует .

Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте ₀, называется резонансом.

При коэффициенте затухания =0, когда отсутствуют силы сопротивления, , а А_рез становится бесконечно большой. На рисунке даны зависимости амплитуды колебаний от частоты вынуждающей силы.