27

1. Кинематика частицы (основные понятия кинематики, прямолинейное и криволинейное движение).

Кинематика – это раздел механики, изучающий движение тел без учета взаимодействия, то есть без учета причин, вызывающих это движение.

Механическое движение – изменение положения тела относительно других тел с течением времени.

Материальная точка – это модель тела, размерами и формой которого можно пренебречь по сравнению с масштабами движения.

Тела отсчета – тела, относительно которых определяется или изучается положение данного движущегося тела.

Система отсчета – это тело отсчета, связанная с ним система координат и способ измерения времени (часы).

Траектория – линия, которую описывает материальная точка в пространстве при движении. В зависимости от формы траектории движение может прямолинейным и криволинейным.

Расстояние, пройденное телом, с момента начала отсчета времени, называется длиной пути. Это длина траектории. Обозначения: длина пути L, S, S.

Вектор, соединяющий начальное положение с последующим положением, называют перемещением. Обозначения перемещения , .

Вектор, соединяющий некоторую фиксированную точку пространства с данной движущейся точкой, назвается радиус-вектором.  , перемещение равно изменению радиуса-вектора.

Введем понятия скорости и ускорения материальной точки. Пусть за промежуток времени t материальная точка переместилась из точки 1 в точку 2 (см. рис.1.2).

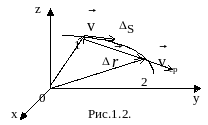
Средняя скорость определяет путь, пройденный в единицу времени. Вектор перемещения  материальной точки представляет собой приращение радиуса-вектора за время t=t₂-t₁: : . Вектор средней скорости _cр: Модуль этого вектора определяется как . Определим вектор скорости материальной точки как предел отношения  /t при t0, то есть . Это значит, что вектор скорости материальной точки в данный момент времени равен производной от радиуса-вектора по времени и направлен по касательной к траектории в данной точке в сторону движения материальной точки. Модуль вектора .

Ускорение – это физическая величина, характеризующая быстроту изменения скорости. Среднее ускорение – это отношения изменения скорости ко времени, за которое это изменение произошло: . Вектор среднего ускорения: , Переходя к пределу, получим вектор мгновенного ускорения: ; т.е. вектор ускорения материальной точки равен производной от скорости по времени.

При использовании декартовой системы координат положение материальной точки задается тремя координатами x, y, z, а при движении точки эти координаты изменяются во времени и, следовательно ее движение описывается тремя уравнениями x(t), y(t), z(t). В этом случае вектор скорости может быть разложен на три взаимно перпендикулярные компоненты: , причем , а вектор ускорения – на компоненты: , причем .

При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения равен пройденному пути, если направление движения не изменяется.

1) В случае равномерного движения:

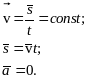В проекции на ось ОХ:

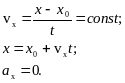
2) В случае равнопеременного движения:

В проекции на ось ОХ:

Криволинейное движение – движение, при котором траектория – кривая линия.

Рассмотрим один из видов криволинейного движения – движение материальной точки по окружности.

1 случай: равномерное движение по окружности, когда скорость по величине является постоянной | |=const, но изменяется по направлению. В этом случае ускорение . Нормальное (центростремительное) ускорение характеризует изменение скорости по направлению. Вектор нормального ускорения направлен по радиусу к центру окружности.

2 случай. Скорость движущейся по окружности материальной точки изменяется по величине и направлению: . В этом случае полное ускорение состоит из двух составляющих:

1. 

   нормальное ускорение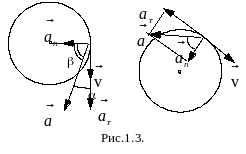 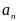– характеризуется изменением скорости по направлению;

2. тангенциальное ускорени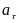е характеризуется изменением скорости по величине.

Так как компоненты и взаимно перпендикулярны, то

Введем векторы угловой скорости и углового ускорения. Вектор угловой скорости определяют как: . Вектор совпадает по направлению с вектором и представляет собой аксиальный вектор. Изменение вектора со временем характеризуется вектором углового ускорения , который определяют как . Направление вектора совпадает с направлением – приращением вектора . Вектор также является аксиальным.

При равномерном вращении =0 и = const.

Кинематическое уравнение равномерного вращения =_о+ t, где _о- начальное угловое перемещение.

Угловая скорость тела при равнопеременном вращении  = _о+t.

Кинематическое уравнение равнопеременного вращения (=соnst)

=_о+ _оt+t²/2,

где _о - начальная угловая скорость.