10.2. Индуктивное обучение

Индуктивное обучение заключается в том, чтобы получить применимые правила из изучения прошлых специфических примеров. Таким образом, индуктивное обучение также называется обучением по примерам. В основу индуктивного обучения положены принципы индуктивных умозаключений. Индуктивным называется умозаключение, в котором на основании принадлежности признака отдельным предметам или частям некоторого класса делают вывод о его принадлежности классу в целом. Полная индукция может быть описана следующим образом:

Посылки: S₁имеет признак Р, S₂ имеет признак Р, S_n имеет признак Р, S₁S₂,...,S_n— составляют класс К. Заключение: Всем предметам класса К присущ признак Р.

Выраженная в посылках этого умозаключения информация служит достаточным основанием для логического переноса признака на весь класс. В случае неполной индукции — на основе принадлежности признака некото­рым элементам или частям класса— делают вывод о его принадлежности классу в целом. Индуктивное обучение может основываться также на анало­гии. Умозаключение по аналогии — это вывод о принадлежности опреде­ленного признака единичному объекту (предмету, событию, отношению или признаку) на основе его сходства в существенных чертах с другим уже из­вестным единичным объектом. Умозаключению по аналогии всегда предше­ствует операция сравнения двух объектов, которая позволяет установить сходство и различие между ними. При этом для аналогии требуется сходство в существенных признаках и различие в несущественных. Рассуждение по аналогии имеет следующую структуру:

Допустим, пользователь желает установить наличие некоторого свойства Q у объекта b, но не имеет такой возможности. Можно использовать подобие объектов b и а. Первые п посылок устанавливают наличие такого подобия, на основании чего делается заключение а = Ь. Далее, опираясь на это заклю­чение о подобии объекта а объекту b, n+1-ю посылку, которая говорит о на-личиии у объекта свойства Q(a), делается вывод о наличии этого свойства у объекта b, т.е. Q(b).

Строгая аналогия имеет место в том случае, если достоверно установле­но, что переносимый признак Т находится в условной зависимости от при­знаков сходства, т.е. (P,Q,S) -> Т.

Различают аналогию свойств и аналогию отношений. В случае аналогии свойств посылки имеют вид:

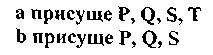
Рис 10.3. Взаимосвязи между элементами схемы индукции

Мы будем рассматривать результат индуктивного как множество правил продукции. Ситуацию обучения мы будем описывать следующим образом: из одного или более примеров, в которых действие (action,) явилось адекват­ной реакцией на ситуацию (situation;) мы делаем вывод, что действие общего вида (action_gen) является адекватным видом реакции на обобщенную ситуа­цию (situation_gen) . При формировании правил вида «если <условие>, то... <действие>, мы будем в зависимости от их адекватности ситуации ослаблять или усиливать их. Антецедент правила является более сильным, если множество его истинности имеет меньшую мощность. Один способ сделать прави­ло более сильным или специализировать его состоит в том, чтобы добавить конъюнкцию.

В общем случае определение понятия применимо к некоторому множест­ву ситуаций, которое называется положительными примерами и не приме­нимо к другому множеству, которое называется негативными примерами. Важными шагами в процессе индуктивного обучения являются процессы генерализации и специализации. Один из путей генерализации — это гене­рализация типа IS-A. Добавление дизъюнкции к концепту делает его более общим, добавление конъюнкции — более специфичным.

Конечным этапом генерализации является универсализация, в результате которой осуществляется переход от единичных примеров к некоторому общему условию, выраженному при помощи квантора общности. Обозначения, используемые для выражения определения понятий, должны обладать свой­ством, что подобные ситуации должны иметь подобные описания и обозначения.

В процессе сравнения абстрактных и конкретных ситуаций мы выделяем абстрактное отображение. Переход от абстрактной ситуации к конкретной есть просто инстанциация, замена переменных константами. Обратный переход есть последовательность генерализаций. Мы будем рассматривать процесс сравнения как модифицированный процесс дедукции, в котором допускается, что цель может быть не достигнута.

Обучение тесно связано с поиском в пространстве состояний. Такой по­иск требует существования множеств операторов, которые трансформируют состояния, проблема поиска заключается в том, чтобы найти последовательность операторов, которые переводят начальное состояние в целевое (же­лаемое), т.е., состояние, которое удовлетворяет описанию цели. Пространст­во, которое подвергается изучению — это пространство «частичных планов» или сеть задач. Операторы сводят задачи к подзадачам и накладывают упо­рядочение на прежде неупорядоченные задачи. Модель мира может быть описана, как конечное множество формул без переменных.

Описание состояния — это конъюнкция литералов, переменные которых интепретируются экзистенциально. Мы будем представлять такие конъюнк­ции как конечное множество литералов.

Целевая конъюнкция G сравнивается с текущим состоянием S. Результа­том сравнения является множество разностей, определенное ниже. Макси­мальная подстановка — это подстановка θ , такая, что для всех других под­становок θ', |Gθ - S׀ < |Gθ'- S|. Здесь мы используем обозначение Gθ для формулы, полученной подстановкой значений переменных в G. Максималь­ная подстановка совпадения — это такая подстановка, которая минимизиру­ет конъюнкции Gθ', не найденные в S.

Разница между G и S — это формула р такая, что для некоторой макси­мальной подстановки совпадения 9, р  Gθ — S. Говорят, что Gθ — S — раз­ностное множество для θ. G совпадает с S точно, если G θ S для некоторого θ. Возможно, что разность G θ - S не выводима (не устранима) в си­туации S.

Мы могли бы попытаться изменить мир, чтобы исключить эту разность, пытаясь элиминировать ее, изменяя определение концепта. Наиболее про­стой путь — удалить избыточные конъюнкции из описания, однако в нашем распоряжении имеются также операции генерализации.

Программа поиска совпадения использует генерализацию, однако про­блема заключается в том, какой из многих возможных вариант специализа­ции затем избрать. Специализация необходима также тогда, когда ситуации совпадают, в то время как они не должны совпадать. Рассмотрим для каждо­го элемента f разностного множества N_θ (f) элементы S, для которых выпол­няется (f). Хороший способ генерализации состоит в том, чтобы найти не­кий суперкласс такой, что заменив им конъюнкции в Gθ и S, мы ликвидиру­ем различие.

Другой возможностью является включение различия в виде дизъюнкции, представляющей исключение из правила вывода. Однако список таких ис­ключений очень быстро разрастается. Важным шагом в поиске совпадений является замена констант переменными. Если в результате многократных сопоставлений обнаруживается, что константы сравниваемых ситуаций, совпадающих в остальном, сопоставимы, то это является свидетельством возможности их вариабелйзации.

Предположим, мы имеем описание желаемой ситуации в виде списка элементарных конъюнкций, имеющих вид (имя атрибута, 'значение атрибута) для исходной ситуации и для целевой. Производя сопоставление каждой из множества данных ситуаций с целевой, алгоритм делит список конъюнкций на два возможно пустых класса — обязательный и желательный. Конъюнк­ции класса «обязательный» должны быть удовлетворены, из конъюнкций класса «желательный» требуется, чтобы совпало максимальное количество элементов.

Понятие соответствия между ситуациями можно рассматривать, используя для этой идеи термин аналогии. Аналогия образует некоторое соответствие или отображение между ситуациями. Это отображение не делает ситуации идентичными, но их различие, возможно, игнорируется. Одна трудность с аналогиями состоит в том, что это отображение может не быть взаимно одно­значным.

Поскольку индивидуально генерируемые правила обычно используются для проблемы классификации, при обучении ставится общая задача полу­чить характеристики не хуже, чем в других статистических методах, таких как статистический дискриминантный анализ.

В отличие от дискриминантного анализа индуктивное обучение не делает никаких допущений априори относительно формы взаимосвязей перемен­ных (например, линейной зависимости). Индуктивное обучение допускает как качественные, так и количественные переменные, и его можно рассмат­ривать как такую же родственную процедуру как дискриминантный анализ.

Такие пакеты, как EXPERT-EASY, VP-Expert, UNIK-INDUCE оборудованы средствами индуктивного обучения.

Предположив, что мы в состоянии решить нетривиальную проблему разработки хорошего языка описания, мы сталкиваемся с вопросом, каким образом можно на этом языке строить нужные описания.

Один из подходов состоит в том, чтобы организовать в пространстве всех возможных описаний поиск таких из них, которые являются и верными, и полезными. Однако число возможных описаний носит астрономический характер, и оно тем больше, чем более выразительным является язык описаний.

Ясно, что должен быть найден какой-то способ управления таким поис­ком, позволяющий избежать рассмотрения громадного числа потенциально возможных описаний (т. е. понятий), которые не имеют отношения к изучаемой в данный момент задаче. Было показано, что этого можно достигнуть многими методами, если использовать незашумленные обучающие последо­вательности. Мы же ограничимся рассмотрением здесь четырех конкретных примеров систем, допускающих использование данных с шумами.

Во всех этих системах обучение правилам классификации происходит в результате рассмотрения цепочки правильно классифицированных обучаю­щих примеров — обучающего множества. При этом предполагается, что та­кие правила впоследствии могут быть применены к новым данным такого же типа, которых не было в обучающем множестве. Правильная классификация лежит в основе многих систем искусственного интеллекта, таких как интел­лектуальные управляющие устройства, системы диагностики, советчики, чувствительные устройства роботов и тому подобные системы.