10.13. Применение алгоритмов типа аво (вычисления оценок) для построения итерационных алгоритмов поиска

В практике поиска необходимо учитывать, что число записей, просмотренных пользователем, и суждение о релевантности которых известно, со­ставляет незначительную часть от общего числа записей базы данных. Снятие этой проблемы связано с отысканием критериев устойчивости статистической выборки по функционалу ошибки. В рассмотренных выше статисти­ческих моделях дескрипторы считались либо независимыми, либо попарно зависимыми. Однако часто поиск пользователем ведется не по отдельным дескрипторам, а по различным их сочетаниям.

Класс АВО исходит из того, что неизвестно, какие сочетания атрибутов наиболее информативны. Поэтому критерию в классе АВО сопоставляются всевозможные комбинации атрибутов и их сочетаний. Пусть даны стандарт­ные описания объектов. Пусть дано множество D объектов d, на этом мно­жестве существует разбиение на конечное число подмножеств (классов)

Разбиение D определено не полностью, задана лишь не­которая информация I_о о классах D_i. Объекты d задаются значениями неко­торых атрибутов x_j, j-l,...,n. Совокупность значений признаков х_j определяет описание I(d) объекта d. Описание объектаназывают стандартным, если x_i(d} приобретает значение из множества допустимых значений.

Таблица 10.4

Таблица обучения

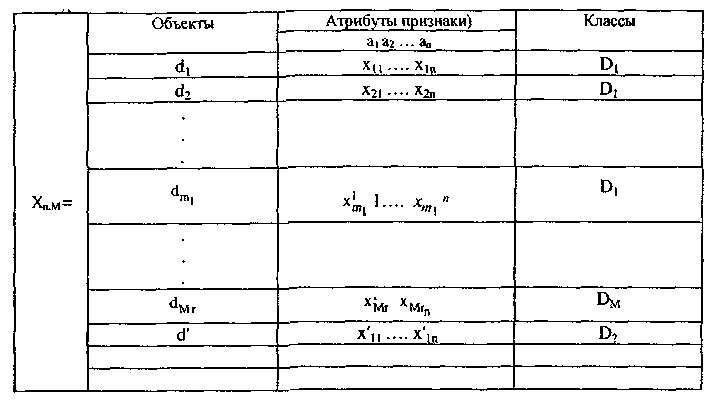
Задача классификации состоит в том, чтобы для данного объекта d и классов D₁...,D_m по описанию I(d) вычислить значения предикатов P_i(d),

. Информация о вхождении объекта d класс D; кодиру­ется символами— не определено и записывается в виде:

Априорная информация в задаче классификации с непересекающимися классами задается в виде таблицы обучения.

Информация о принадлежности объекта классу записывается в виде:

Пусть определена некоторая мера близости объекта d к тому или иному классу, называемая обобщенной оценкиобъектаd' по классу D_i

Описания объектов классификации переводятся в матрицу оценок

В основе тестовых алгоритмов лежит понятие теста. Тестом таблицы Х_n,_м называется совокупность столбцов а_t1...,а_tq, таких, что после удаления из Х_n,_м всех столбцов, за исключением имеющих номера ti,...,t<, в полученной таблице X_n-q,_M все пары строк, принадлежащих разным классам, различны. Тест {x_t1,...,x_tq} называется тупиковым, если никакая его часть не является тестом.

Пусть {Т} — множество всех тупиковых тестов Т_пт и Т{ x_t1,...,x_tй } {T}. Выделим в описании классифицируемого объекта I (d'^} часть { x'_t1 ...,x'_t } со­ответствующую атрибутам x_t1,...,x_t и сопоставим ее со всеми частными описаниями (х_rt1 ,...,х_rtq ) объектов I(dr) таблицы

Подсчитаем число совпаденийчастичных описаний (x'_t1 ,...,x'_t ) со

всеми частичными описаниямиобъектов i-ro класса. Величина

F_T{d, D_i) представляет число строк этого класса, близких классифицируемой строке d' по тесту Т. Аналогичным образом вычисляется оценка для d' по остальным тестам (для всех классов).

Величина F(d', представляет собой оценку объекта

d' по классу D_i. При вычислении оценок могут быть учтены веса или важ­ность атрибутов. Одной из естественных мер важности признаков является

информационный вес где г (n,m) — число тупиковых тестов

таблицы Х_n,m, r_aj.(n,m)- число тупиковых тестов таблицы T_n,m содержащих

атрибут a_j, чем больше его информационный вес p(a_j), тем значительнее роли в описании объектов.

Переход от тестовых алгоритмов к АВО связан с расширением видов подмножества атрибутов, по которым производится сопоставление класси­фицируемого объекта с объединениями из X_n,m и построением оценок опор­ных множеств.

Системы опорных множеств составляются из всех подмножеств множе­ства атрибутов фиксированной длины q, q=2,..., m-1, либо из всех непустых подмножеств множества атрибутов.

Рассмотрим полный набор атрибутов <а₁ . . ., а_n> и выделим систему

опорных множеств S₁ . . ., S_L. Удалим произвольный поднабор признаков из строк d₁, d₂,..., d_rm, d' и обозначим полученные строки x_d1 ,x_d2 ,...x_drm x_d

Правило сходства, позволяющее оценить похожесть строк x_d1 и x_d2 состоит в

следующем. Пусть усечение строки содержит q первых признаков, т.е. x_dr = (x₁,...,x_q) и x_d, = (х₁...,х_q) и заданы пороги Е₁,...,Е_q,. Строкиx_d. и х_dr считаются похожими, если выполняется не менее б неравенств вида Величины Е₁,...,Е_q , входят в качестве параметров в модель класса алгоритмов типа АВО. Рассмотрим процедуру выполнения оценок по подмножеству S₁. Для остальных подмножеств она полностью аналогична. В матрице X_n,m выделяются столбцы, соответствующие атрибу­там, входящим в S₁, остальные столбцы вычеркиваются. Проверяется бли­зость строки x_ld. со строками x_ld ,...,x_ld , принадлежащему классу Ω_1. Число строк этого класса, близких по выбранному классифицируемой строке х_1d, обозначается F_s1 (d¹, D₁), эта величина представляет собой оценку строки d' для класса D₁ по опорному множеству S₁. Аналогичным образом вычис­ляются оценки для остальных классов: F_s1 (d',D₂),...,F_s1 (d',D_m) . Применение подобной процедуры ко всем остальным опорным множествам алгоритма позволяет получить систему оценок

Величины

представляют собой оценки строки d' для соответствующих классов по сис­теме опорных множеств алгоритма S_A. На основании анализа этих величин принимается решение либо об отнесении объекта d' к одному из классов D_i, i=l,...m, либо об отказе от классификации.

Пример 10.1. Задана таблица обученных и классифицированных запро­сов. Пусть

Таблица 10.5

Поскольку заносятся в класс 2.

Сложностьформулы вычисления оценок АВО при произвольнойS_A пропорциональные сложности ДНФ, представляющей характеристиче­скую функцию систем опорных множеств алгоритма. Это означает, что построение простой формулы вычисления оценок F(d'', D_i) связано с за­данием минимизации булевых функций в классе ДНФ, а точнее с задани­ем построения кратчайшей ортогональной ДНФ или ДПФ, в которой каждая элементарная конъюнкция имеет небольшое число общих перемен­ных с соседними.