10.16. Алгоритмы автоматического построения классификаций

Автоматическая классификация объединяет весь набор методов и алгоритмов, предназначенных для разбиения совокупности объектов, каждый из которых описан набором переменных на какое-то число однородных (в определенном смысле) классов. Эти классы могут быть в той или иной степени связаны между собой, например в форме графа или дерева, каждая вершина которого представляет один класс.

После выбора атрибутов, способа представления их весов в документах и единиц измерения, информация о каждом признаке любого объекта записывается в таблицу, в которой множество строк представляет индивидуумы (объекты), а множество столбцов — признаки (дескрипторы).

Кластеризация— это разновидность классификации, определяемой на конечном множестве объектов. Отношения между классифицируемыми объ­ектами представлены в виде матрицы близости, в которой строки и столбцы соответствуют объектам. Мы различаем иерархическую и партициональную кластеризации. Иерархическая кластеризация— это последовательность разбиений, в которой каждое разбиение вложено в последующее разбиение в последовательности.

Общее описание методов партициальной кластеризации

Наиболее широко используемые методы кластеризации основываются на критерии квадратичной ошибки. Общая цель состоит в том, чтобы получить разбиения, которые для фиксированного числа кластеров минимизируют квадратичную ошибку. Предположим, что дано множество п образов в от

измерениях, каким-либо способом разбитое на к кластеров {S₁,S₂,...,S_k}, таких, что кластер S_i имеет n_i образов (рис. 10.13).

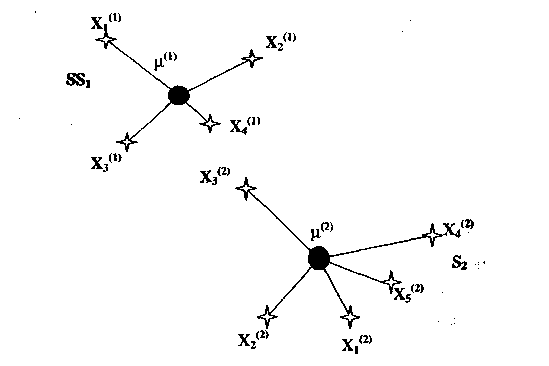
Рис. 10.13. Расстояния, используемые при вычислении квадратичной ошибки

При этом

Средний вектор или центр кластера Sj определяется как центроид класте­ра или

где x₁ — 1-й образ, принадлежащий кластеру S_i.

Квадратичная ошибка для кластера S_i есть сумма квадратов эвклидовых расстояний между каждым образом в S_i и центром кластера ⁽ⁱ⁾. Эта квад­iратичная ошибка называется также внутрикластерной дисперсией

Квадратичная ошибка для всего разбиения, содержащего к кластеров, есть сумма внутрикластерных дисперсий:

Цель процедуры кластеризации, основанной на квадратичной ошибке, — найти разбиение, содержащее к кластеров, которые минимизируют Е для фиксированного к. Результирующее разбиение называется также разбиением минимальной дисперсии. Другими словами, образы рассматриваются как коллекция к сферически распределенных сгустков. Кластеризация по крите­рию минимальной ошибки пытается создать к групп, насколько это возмож­но более компактных и взаимно удаленных.

Алгоритм партициальной кластеризации. Метод k-средних (k-means)

Алгоритм k-внутригрупповых средних является алгоритмом построения неиерархической классификации. Основная идея алгоритма заключается в том, чтобы найти некоторое начальное приближение и перемещать реализа­ции из одной группы в другую так, чтобы улучшить значение функции кри­терия.

Пусть X — выборка точек, подлежащих классификации.

Шаг 1. Выберем k исходных центров классов ⁰₁,...⁰_k. Этот выбор производится произвольно, и обычно в качестве исходных центров используются k элементов выборки.

Шаг 2. На m-ом шаге заданное множество точек X разбивается на к клас­сов S^m₁,...,S^m_k по правилу xS₁ ^m, если для всех

— множество точек, входящих в класс с центром _j^m . В случае равенства решение принимается по жребию.

Таким образом, правило формирования классов выглядит следующим образом:

Шаг 3. После того как построение на шаге 2 выполнено, на основании

его результатов определяются новые центры классов

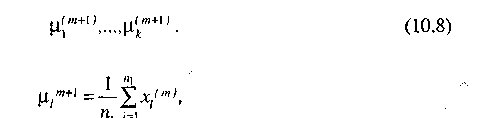
где n, — число точек в классе

Выбор новых центров классов производится исходя из условий, что сумма квадратов расстояний между всеми точками, принадлежащими множеству S₁^m , и новым центром класса должна быть минимальной. Другими словами, новые центры классов выбираются так, чтобы минимизировать показатель качества

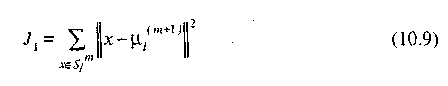
₁ ^(m+1), обеспечивающий минимизацию показателя качества, является, в сущности, выборочным средним, определенным по множеству S₁^m.

Шаг 4. Еслито возвращаемся к шагу 3, заменив m

на т+1. Если S^m+1=S^m, тo полагаем S^m=S* и заканчиваем работу алгоритма.

Равенство j ^(m+1) = _j^m при j=l,2,...,k является условием сходимости алго­ритма. При его достижении выполнение алгоритма заканчивается. Качество работы алгоритма, основанного на выполнении к средних, зависит от числа выбираемых центров классов, от выбора исходных центров классов, от последовательности осмотра объектов.