7.6. Логика веры и знания

В рамках логики веры и знания оператор D принимает соответственно зна­чения «предполагается» и «известно». Двойственный оператор 0, соответствен­но, «противоположное не предполагается» и «противоположное неизвестно». Бинарные отношения и схемы формул:

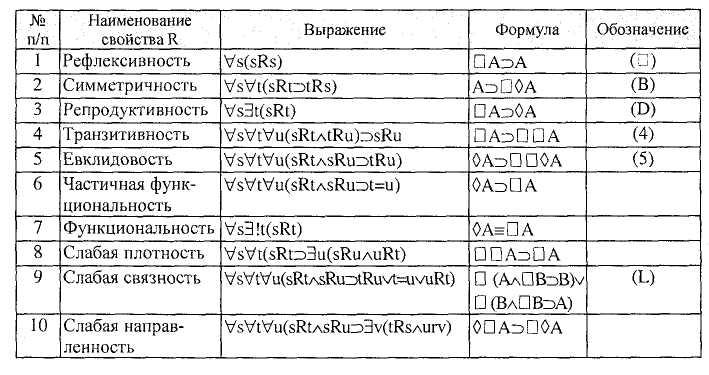
Следует отметить, что такие свойства бинарного отношения как иррефлексивность , антисимметричность , асиммет­ричность не имеют модальных аналогов.

Теорема 1. Формула А является теоремой логики КТ тогда и только то­гда, когда А истинна во всех случаях, в которых R рефлексивно.

Теорема 2. Формула А является теоремой логики S4 тогда и только тогда, когда А истинна во всех структурах, в которых R рефлексивно и транзитивно.

Теорема 3. Формула А является теоремой логики S5 тогда и только то­гда, когда А истинна во всех структурах, в которых R рефлексивно, транзитивно и евклидово (т.е. R — отношение эквивалентности).

Т — требует в логике знания чтобы «то, что известно, является истинным» (KAA). Напротив Т не будет фигурировать в системе аксиом, форма­лизующих веру. Схема 4 — схема позитивной интроспекции КАККА. Схема 5 формализует негативную интроспекцию ВАКВА, или KAKKA. Схема 5 означает «если я не верю, что А подтверждается, то я знаю, что не верю, что А подтверждается». Каждая из этих различных модальных систем индуцирует синтаксическое отношение выводимости, которое ей свойственно. Оно обозначается символом ├_s, где S — название рассматриваемой модальной системы.

Обычно принято представлять наименьшую нормальную логику, содер­жащую схемы Σ₁ ..., Σ _n с помощью обозначения Λ = k Σ₁,..., Σ _n.

Классическими обозначениями для некоторых схем являются следую­щие:

D: □А◊А

□ : □AA

4: □А□□А

В: А□◊А

5: ◊А□◊А

L: □ ((A□A) B) □ ((B□B) A)

W: □ (□АА) □А

Для некоторых широко используемых логик применяются такие обозна­чения:

S4: КТ4

S5: КТ45

Моделью М логики первого порядка α (без равенства) называется пара (S, V), где S — область интерпретации и V — функция, совпадающая с функцией интерпретации I. Правила интерпретации определяют семантику языка предикатов. Эти правила базируются на интерпретации I, заданной как тройка (S, I_С, I_о), где S — непустое множество элементов (область интерпретации, I_С — функция, т.е. оценка, которая приписывает определенные знания предикатным и функциональным константам, I₀ — функция назначения, которая каждой индивидной константе ставит в соответствие некий элемент из S). Роль функции V состоит в том, чтобы интерпретиро­вать функциональные и предикатные константы языка в терминах элемен­тов области S.

Определение семантики в рамках этой модели требует еще и определение некой функции q, которая присваивает значения переменным языка. Семантика формул из α описывается с помощью обозначения: М ╞_q А, которое оз­начает «А истинна в модели М для присваивания q».

Описание закономерностей и взаимосвязей предметной области в виде высказываний на языке исчисления предикатов с использованием модальностей, временных соотношений повышает выразительные возможности языка и адекватность представления знаний об объекте в интеллектуальной ин­формационной системе.