С предприятием «Гран» не может быть заключен новый контракт.

Отношение логического следования между посылками и заключением предполагает связь между посылками по содержанию. Если суждения не связаны по содержанию, то вывод из них не возможен.

В зависимости от строгости правил вывода различают два вида умозак­лючений: демонстративные (необходимые) и недемонстративные (правдоподобные). Демонстративные умозаключения характеризуются тем, что заключение в них с необходимостью следует из посылок. В недемонстра­тивных умозаключениях правила вывода обеспечивают лишь вероятное сле­дование заключения из посылок. Различают дедуктивные (от общего знания к частному) выводы, индуктивные (от частного к общему), умозаключения по аналогии — абдуктивные (от частного к частному).

Сложным называют суждение, состоящее из нескольких простых, связанных логическими связками. В соответствии с дедукциями логических связей различают следующие виды сложных суждений: (1) соединительные, (2) разделительные, (3) условные, (4) эквивалентные. Истинность данных сложных суждений определяется истинностью составляющих их простых.

Соединительным или конъюнктивным называют суждение, состоящее из нескольких простых, связанных логической связкой «И».

Например: «Овощи и фрукты продаются в этом магазине». В естест­венном языке конъюнктивная связка может быть представлена такими выражениями, как: «а», «но», «а также», «как и», «хотя», «однако», «несмотря на», «но», «одновременно» и другими.

Соединительное суждение истинно при истинности всех составляющих его конъюнктов и ложно при ложности хотя бы одного из них.

Разделительные (дизъюнктивные) суждения. Разделительным, или дизъюнктивным, называют суждение, состоящее из нескольких простых, связанных логической связкой «ИЛИ».

Например: суждение «Договор купли-продажи может быть заключен в устной или письменной форме» является разделительным суждением, состоящим из двух простых: «Договор купли-продажи может быть заключен в устной форме»; «Договор купли-продажи может быть заключен в письменной форме».

Следует различать: нестрогую (слабую) дизъюнкцию и строгую (сильную) дизъюнкцию.

Нестрогая дизъюнкция — суждение, в котором связка «ИЛИ» употребляется в соединительно-разделительном значении.

Например: «Магазин торгует овощами или фруктами». «В магазине всегда имеются в наличии овощи или фрукты».

(2) строгая дизъюнкция — суждение, в котором связка «ИЛИ» употребляется в разделительном значении.

Например: «Деяние может быть умышленным или неосторожным.

Разделительная связка в языке обычно выражается с помощью союзов «или», «либо». Поскольку в грамматике отсутствуют однозначные союзы для нестрогого и строгого разделения, то вопрос о типе дизъюнкции в юридических и других действиях должен решаться содержательным анализом соответствующих суждений.

Условным или импликативным называют суждение, состоящее из двух простых, связанных логической связкой «если..., то...». Например: «если сделка признана неудачной, то потерпевшему возвращается другой стороной все полученные ею по сделке». Первое суждение называют антецеден­том (предшествующим), второе консеквентом (последующим) импликативное суждение записывается формально в виде р q или в виде р q .

Истинность импликации объясняется следующим образом: истинность антецедента достаточна для признания истинности консеквента.

В естественном языке в условных суждениях используется не только со­юз «если..., то ...», но и другие союзы: «там..., где...», «тогда..., когда...», «постольку..., поскольку...» и т.п.

В форме условных суждений в языке могут быть представлены другие виды объективных связей, как причинные, функциональные, пространственные, временные, правовые, семантические, логические и другие зависимости.

В текстах естественного языка в форме условных суждений нередко фиксируют правовые предписания: разрешения, запрещения, обязывания. Грам­матическими показателями импликации могут служить помимо союза «ес­ли..., то...», такие словосочетания, как «при наличии... следует...», «в фор­ме... следует...», «при условии... наступает...» и другие.

Например: «В случаях, когда своевременно направленное извещение об акцепте получено с опозданием, акцепт не считается опоздавшим, если сторона, направившая оферту, не уведомит другую сторону о получении акцепта с опозданием».

В условном суждении антецедент выполняет функцию фактического или логического основания, обусловливающего принятие в консеквенте соответствующего следствия.

Эквивалентным называют суждение, включающее в качестве составных два суждения, связанные двойной (прямой и обратной) условной зависимостью, выраженной логической связкой «если и только если..., то...».

В естественном языке, в том числе и в нормативных актах, для выраже­ния эквивалентных суждений используют союзы: «лишь при условии, что... то...», «в том случае и только в том случае, когда..., тогда...», «только тогда, когда..., то... и другие».

Например:

«Меры по санации предприятия могут быть приняты только при нали­чии достаточных оснований».

Для того, чтобы иметь возможность в ИИС оперировать с знаниями и фактами, подобно тому, как это делает человек в соответствии с законами формальной логики, необходимо переложить правила и законы логики на строгий математический язык. Такой формальный язык должен быть свободен от нестрогости и неоднозначности естественного языка. Формализован­ный язык должен позволять пользователю ИИС обращаться с запросами к базе данных.

В формализованных языках имеются четкие и эффективные правила построения форм высказываний, причем каждое правильно построенное выражение этого языка имеет единственно возможную смысловую интерпретацию. В основе формализованного языка лежит исчисление предикатов. Для построения формализованного языка мы, прежде всего, должны определить его алфавит. В соответствии с разработанной концептуальной схемой базы данных выделяется фиксированное множество объектов (за­писей), отношений (предикатов) и функторов, отображающих объекты на объекты. С помощью предикатов, функторов, индивидных переменных, индивидных констант, используя допустимые правила комбинирования в соответствии с формальным синтаксисом, мы формируем последователь­ности знаков.

Общая схема построения такого формализованного языка состоит в следующем:

Сначала задается его алфавит — совокупность простейших исходных символов, из которых строятся выражения языка. В алфавит включаются логические символы — специальные знаки для логических терминов, нелогические символы — параметры, предназначенные для замещения простых вы­сказываний или нелогических терминов различных категорий, технические символы, например скобки. Далее определяются правила образования из ис­ходных символов различных типов выражений данного языка, в частности, задается класс формул, посредством которых фиксируются логические фор­мы высказываний.

В рамках формализованного языка ^строятся логические теории, решающие следующие задачи:

• выделяют во множестве формул языка класс формул, представляющих собой логические законы;

• определяют правила логического вывода от совокупности формул F₁ , F₂, …., F_m (посылок) к формуле F_n ( заключению).

Основную компоненту логической теории называют машиной вывода. С одной стороны, знание должно храниться в компьютере в некоторой удобной форме представления; с другой стороны, системе необходимы средства навигации и манипулирования знаниями.

Функтор задает отображение области D в некоторую область R, заметим, что m-местный функтор может быть заменен m + 1-местным предикатом, но не наоборот. Например, вес (станка) — 5т, цена (книги) = 10 р. — примеры одноместных функторов, которые можно заменить двухместными предикатами: вес (станок, 5т), цена (книга, 10 р.). Функтор имеет интенсионал и экстенсионал. Интенсионал относится к тому, что обозначается или заклю­чено в самом функторе, т.е. касается оператора в левой части. Вся левая сто­рона называется выражением функтора. Экстенсионал в каждом случае — значение правых частей.

Алфавит формализованного языка содержит множество свободных индивидных переменных (переменные при их интерпретации в качестве элемен­тов отношений могут пробегать значения строк отношения «строковые пе­ременные», либо значения строк в одном столбце (домене) отношения «срез строковой переменной»).

Переменные могут относиться к различным отношениям или типам, так как они могут пробегать значения из разных отношений.

Множество типов составляет следующую группу симво­лов. Примерами типов могут быть: страна, город, вид изделия.

Y — множество связанных индивидных переменных;

Ф_т— множество m-местных функторов; т = 0, 1, 2...;

Р_т — множество m-местных предикатов;

L — множество связок, состоящее из символов

Q — множество символов кванторов, куда входят квантор существо­вания , которому в естественном языке соответствует термин «существует» и универсальный квантор или квантор общности , которому соответству­ет термин «для всякого». Вообще говоря, состав кванторов может быть ши­ре, например: «по крайней мере и», «ни один», «самое большее и», «точно и», «п процентов», «никакой», «только п».

В состав языка включаются также скобки { () }. Объединение всех этих множеств называется множеством знаков алфавита. С помощью предикатов, индивидных констант, используя допустимые правила комбинирования, мы формируем последовательности знаков, называемых термами. В общем случае терм соответствует определению новых переменных, производных от индивидных, задаваемых преобразованиями, которые определяются функторами. В случае языка прикладного исчисления предикатов термами исчислениями являются константы и переменные (в отсутствие функторов). Разли­чаются первичные (примитивные) термы, которыми являются свободные переменные, константы и выражения вида (х₁, х₂, ..., х_т), где — знакт-местного функтора, х₁, х₂, ..., х_т — свободные переменные и составные тер­мы, т.е. термы, в состав которых входят другие термы.

Следующий уровень языка связан с формированием пропозициональных функций, в которых переменные пробегают некоторое фиксированное множество объектов. Если в пропозициональную функцию подставить конкрет­ные значения переменных, то получим предложение (суждение). Предложе­ние может быть истинным или ложным по отношению к такой подстановке. Можно рассматривать суждения как частный случай пропозициональных функций с пустым множеством переменных. Элементарные формулы можно рассматривать как переменные высказывания или предложения, утвер­ждающие, что выраженные предикатами отношения справедливы для объек­тов, соответствующих термам. С помощью пропозициональных связок, кванторов, символов предикатов, используя элементарные формулы, можно формировать более сложные пропозициональные функции, которые назы­ваются просто формулами. Примитивной формулой называют в отсутствие функторов цепочку символов вида (x₁, x₂, ..., х_n), где —n-местный преди­кат (реляционный оператор), x₁, х₂,..., х_n — свободные индивидные перемен­ные. Заметим, что при интерпретации элементарная; формула определяет элементарное условие запроса, если интерпретировать предикаты как отношения базы данных, переменные — как пробегающие значения доменов или строк этих отношений.

Более точно, множеством примитивных термов, образованных из знаков алфавита, называется наименьшее множество Т (конечных последовательностей знаков из А), такое, что все свободные индивидные переменные и все нульместные функторы принадлежат Т.

Если t-примитивный терм со свободными индивидными переменными х_1, х₂, ..., х_т и t_1, t₂ >….., > t_m принадлежит T, то результат подстановки t₁, t₂, ..., t_m соответственно х₁, х₂, ..., х_т в t также принадлежит Т. Если в А нет функто­ров, то множество всех термов Т совпадает с множеством свободных индивидных переменных. Под примитивной формулой мы будем понимать лю­бую конечную последовательность знаков из А вида Р(х₁, х₂, ..., х_т), записан­ную в виде Р(Х), где Р — m-местный предикат (т = 1,2,...), а х₁, х₂, ..., х_т — свободные индивидные переменные. Дадим более точное определение фор­мулы.

Множеством формул, образованных из знаков алфавита А, называется наименьшее множество F конечных последовательностей знаков из А, такое, что:

• если — примитивная формула со свободными переменными х_ь х₂,..., х_т, a t₁, t₂, ..., t_m — термы, то результат подстановки термов t₁, t₂, ..., t_m вместо х₁, х₂,..., х_т в принадлежитF;

• если принадлежитF и 0 — знак какой-нибудь унарной пропозицио­нальной связки (отрицания), то 0 также принадлежит F:

• если и принадлежатF и 0 — знак какой-нибудь бинарной пропози­циональной связки (), то (0 ) также принадлежит F;

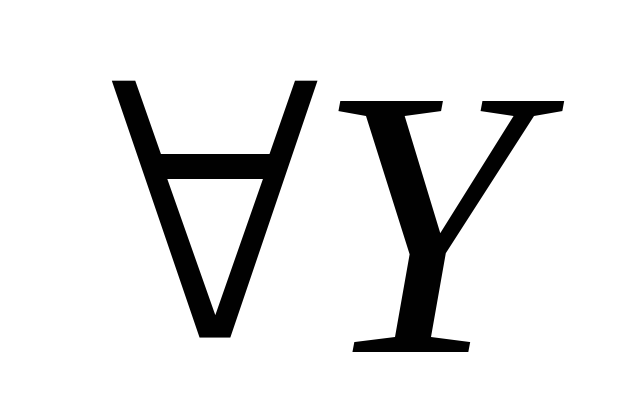
• если (Х), где X — обозначает некоторую свободную индивидную пере­менную и принадлежит F, то при любой связанной индивидной перемен­ной, которая не встречается в (Х), выражение Y(y), (y), принад­лежит F.

Система L = (А, Т, F) называется элементарным формализованным языком первого порядка, основанном на алфавите А.

Переменная X является свободной в формуле Р(Х), если Р(Х) содержит X и не содержит квантора, связывающего X. Если Р(Х) содержит X и X не свободен в Р(Х), тогда X — связан в Р(Х). Переменные, свободные для всей формулы, называются свободными. Заметим, что семантика кванторов определяется соотношениями:

хР(х)=Р(с₁)Р(с₂) ...Р(с_m),

где с_i, 1 im — значения переменной

xP(x)=P(c₁) P(c₂) ...P(c_m).

Таким образом, для проверки выполнения квантора общности требуется проверка значения предиката для всех значений переменной. Проверка выполнения условия, содержащегося в кванторе существования, производится до первого сравнения, т.е. первой строки отношения, для которой выполня­ется указанное условие.

При использовании языка, основанного на исчислении предикатов, мы хотим, чтобы пользователь лишь записал условия, связывающие переменные и целевой список переменных, в то же время преобразование этой формулы в последовательность операций над отношениями базы данных должно осуществляться автоматически.

Построение исчисления требует установления определенных отношений между формулами (эквивалентность, выводимость). Исчисление предикатов является частным случаем формальной системы.

Пусть L — формализованный язык, В_о — множество формул. Определим операцию присоединения следствий к L, которая каждому множеству формул Ф в L сопоставляет множество С(Ф) всех конечных следствий из фор­мул, принадлежащих L на основании понятия вывода. Для этой цели будет выбираться множество R логических аксиом, т.е. некоторых формул из L истинных в силу своего синтаксического строения и будут введены некото­рые правила вывода. Формальная система представляет собой формализа­цию некоторой теории, образуя синтаксис последней. Теория же образует интерпретацию данной формальной системы.

Для произвольного множества формул Ф мы определяем С(Ф) как наи­меньшее множество формул, содержащее Ф и замкнутое относительно пра­вил вывода (транзитивное замыкание отношения выводимости).

Любая пара D = {L, С}, где L — формализованный язык, а С — операция присоединения следствий в L, называется дедуктивной (формализованной) системой. Под формализованной системой мы будем понимать любую тройку S = {L, С, R}, {L, С} — некоторая формализованная система, R — множество аксиом этой теории. Операция присоединения следствий называется также логикой теории.

Для того чтобы преобразовать прикладное исчисление предикатов в язык запросов, необходимо придать интерпретацию свободным переменным, определить перечень доступных предикатов и связать исчисление с реляцион­ной базой данных.

Будем интерпретировать функторы и предикаты как символы конкретных отображений и отношений. Сопоставим каждому m-местному функто­ру отображение у^m у, т.е. сопоставим каждому функтору тип выпол­няемой операции, например, «сумма», «итого», «процент», max, min либо значение атрибута. Каждому m-местному предикату Р сопоставим m-местную у таблицу (отношение) с атрибутами (домены с соответствующи­ми указателями роли) в у. Заметим, что в формализованном языке связан­ные переменные определяют условия поиска, а свободные переменные — условия выдачи.

Для того чтобы преобразовать прикладное исчисление предикатов в язык запросов, необходимо:

• придать интерпретацию переменным;

• определить конкретные виды доступных предикатов;

• связать универсум исчисления с реляционной базой данных.

Чтобы представить целевой, т.е. подлежащий выдаче список объектов, исчисление интерпретируется следующим образом.

Формула, содержащая свободные переменные, получает значение истинности на кортежах реляционной таблицы, когда каждая переменная в ней поочередно заменяется элементом соответствующего кортежа. Например, {(x, y)│F(x, у)} обозначает множество тех пар элементов из универсума D, что формула F со свободными переменными истинна для каждой из пар, когда первый элемент пары замещает вхождение х в F, а второй элемент — вхож­дение у.

Семантика типового исчисления предикатов определяется как отображение D₁х ... х D_n —> {истина, ложь}, в то время как семантика бестипового исчисления предикатов — как отображение Dⁿ —> {истина, ложь}. Только те предикаты Р(А₁/,..., А_п/)являются правильно построенными, для которых терм A_i,- имеет тип _i. В зависимости от способа определения переменных и способа записи формул различают язык запросов, ориентированный на кор­тежи, и язык запросов, ориентированный на домены. Общение пользовате­лей-непрограммистов с реляционной базой данных осуществляется с помо­щью языка запросов высокого уровня.

Основанные на непроцедурных системах языки запросов являются языками высокого уровня, они освобождают пользователя от необходимости определять состав операций для получения желаемого ответа. В основе логической обработки данных, использующей знания и применяющей правила дедуктивного вывода, лежит язык исчисления предикатов первого порядка.

Язык включает знаковые выражения нескольких видов: индивидные, функциональные, предикатные, логические технические.

Индивидные имена (константы) есть выражения, обозначающие объекты, индивиды. Например, завод «Красный пролетарий», фамилия «Ива­нов». Индивидные переменные — это выражения, которые сами по себе не обозначают объекты, но каждому из которых сопоставляется некоторая область (тип) объектов, что может записываться в следующем виде: x₁/фирма, х₂/изделие. Это означает, что переменная x₁ пробегает область значений «фирма», а переменная х₂ — область значений «изделие». В любом выражении, содержащем индивидную переменную, эту перемен­ную можно заменить именами объектов из некоторой рассматриваемой области.

Функциональные символы — это выражения, которые именуют функции, сопоставляющие наборам из п индивидов некий индивид. Например, если область объектов составляют числа, то примером функции на этой об­ласти будет сложение — функция, сопоставляющая паре чисел некоторое число.

Предикатные символы — это выражения, обозначающие свойства и отношения. Предикаты могут быть одно-, двух- и вообще n-местными. Напри­мер, «завод Красный пролетарий» производит станки» — пример двухмест­ного предиката, «фабрика «Заря» поставляет обувь универмагу «Москва» — пример трехместного предиката.

Логические связки или пропозициональные константы служат для образования из одних формальных выражений языка, атомарных или простых, других, более сложных выражений этого языка. Мы будем использо­вать обычные логические связки: — конъюнкция,— дизъюнкция,—импликация, — отрицание.

Кванторы — это знаки, которые в сочетании с переменными дают возможность выразить утверждения о том, что для всех или для некоторых ин­дивидов выполняются определенные условия. Знак квантора всеобщности возник как сокращение слова Аll («все»), а знак квантора существования — как сокращение слова Exists («существует»). Последний тип знаков — технические знаки: скобки правая «)», левая «(« и запятая «,». С помощью знаков этого типа выражения однозначно расчленяются на составляющие части (подвыражения). С помощью индуктивного определения введем поня­тие терма:

• индивидные константы и индивидные переменные суть термы;

• если f есть k-местная функциональная константа и t₁...,t_kтермы, не обяза­тельно различные, то P(t₁...,t_k) есть терм, никакое другое выражение, кро­ме указанных, не есть терм.

Теперь индуктивным путем введем понятие формулы.

1. Если Р есть k-местная предикатная константа, и t₁...,t_k_ термы, то P(t₁,...,tk) есть атом.

2. Атом есть формула.

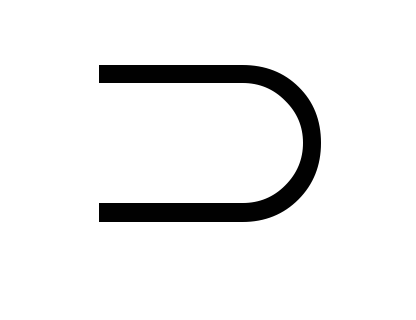3. Если F и G — формулы, то F, FG,FG,FG и F 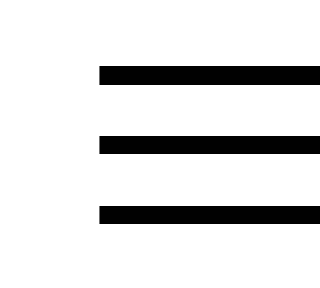G — формулы.

4. Если F — формула и х — связанная индивидная переменная, то xF и xF — формулы.

Формулы порождаются конечным числом применения правил 1—4.

Будем говорить, что вхождение некоторой переменной в формулу F находится в области действия квантора по х, если это есть вхождение в подформулу формулы вида xA или хА. Вхождение переменной х в формулу А будем называть свободным, если оно не находится в области действия квантора по х, и связанным — в противном случае.

Подстановкой вместо свободной переменной х терма t в выражение А будем называть замещение каждого вхождения свободной переменной х в А на терм t. Операцию подстановки будем обозначать F_tA. Если фор­мула не содержит свободных вхождений связанных переменных, то она называется замкнутой формулой или предложением. Правило импликации, записываемое в виде pq, выражает структуру логических рассуж­дений. Первый его операнд называется посылкой или антецедентом, и второй — заключением или консеквентом. Импликация, называемая также материальной импликацией, является основной связкой в мате­матических рассуждениях. Она соединяет условие и утверждение в тео­реме. В таблице 7.1 представлены значения истинности для логических связок.

Таблица 7.1