7.5. Немонотонные выводы

Обычные дедуктивные системы логики не позволяют прямо формализовать модифицируемые рассуждения. Они обладают свойством монотонности: множество теорем растет лишь с увеличением множества основных аксиом.

В формальной системе дедукции определено отношение выводимости -, которое:

• рефлексивно: {р₁ ...,p_n,q} |-q,

• монотонно: если {p₁, ...,p_n,q} |-q, тo{p₁, ...,p_n} -q,

• транзитивно: если { p₁, ...,p_n} -r и{ р₁ ..., p_n,r} |-q,

• тo{p₁,...,p_n}|-q.

Здесь р₁ ..., p_n, q, r — формулы рассматриваемого логического языка.

Отношение семантического следования |= между множеством посылок А и заключением р определяется как : А |= р, если любая модель для А является моделью для р.

Немонотонные логические системы — это логики, в которых введе­ние новых аксиом может уточнить старые теоремы. Такие логики очень важны при моделировании реальных процессов, которые в присутствии неполной информации могут создавать и затем пересматривать предполо­жение в свете новых наблюдений. Неудовлетворенность обычной логикой состояла в том, что было неясно, как работать с неполным знанием. В об­ласти искусственного интеллекта изучение восприятия, неоднозначности и общеизвестных знаний привело к представлению знаний с эксплицитным включением информации относительно типичных случаев ошибок и методов обработки ошибок. Много работ было выполнено по автоматическому доказательству теорем для исчисления предикатов первого порядка. Не­полная информация представлена в этих системах как дизъюнкция не­скольких возможностей, но отдельные дизъюнкты могут быть независимы от этих аксиом.

Для того чтобы не перечислять в базе знаний все неполные знания, все, что неопределенно, считают заведомо ложным. Это называют гипотезой закрытого (ограниченного) мира (closed world assumption).

Классическая логика исходит из предпосылки, что набор определенных в ней аксиом (знаний) полон, и истинность вывода не нарушается, даже если впоследствии добавляется новая аксиома. Такое свойство называется монотонностью.

Классическая символическая логика не располагает средствами для описания того, как скорректировать имеющуюся формальную теорию, чтобы иметь возможность учесть противоречия, вызванные поступлением новой информации. Дело заключается в том, что сделать выбор между альтерна­тивными вариантами пересмотра имеющихся аксиом очень трудно.

Важным шагом на пути к этому является введение двух различных про­блем, которые могут быть названы пересмотр процедур и реорганизация модели мира.

Традиционные логики являются монотонными вследствие того, что теоремы теории всегда являются подмножествами теорем любого расширения теории. В данной статье под теорией мы понимаем множество аксиом. Более точно, выражение монотонности заключается в следующем: если А и В — две теории и АВ, тогда Th(A)Th(B), где Th(S)={p:S - р} — множество теорем S. Монотонные логики имеют тот недостаток, что при поступлении новой информации необходимо всякий раз пересматривать существующие выводы. Понятие немонотонной логики вводится, отправляясь от классиче­ских логик, путем их расширения за счет введения модальностей, в частно­сти, модальности «консистент» (совместный), которая обозначается М. Не­формально Мр обозначает, что р совместно со всеми теоремами. Будем ис­пользовать обозначение Lp для выражения Mp, читая Lp как («возможно совместно р»).

Пусть L — язык упомянутых теорий, который имеет бесконечное число знаков констант, знаков переменных предикатных символов.

Правила образования правильно построенных формул такие же, как в исчислении предикатов первого порядка, рассмотренных нами ранее.

К числу формул в немонотонной логике добавляется цепочка Мр. Переменная х свободна в Мр если и только если х свободна в р. Символы С, D, Е, F — будут использоваться как синтаксические переменные, изменяющиеся по пропозициональным символам констант. Буквы р, q и г будут использо­ваться для формул. Если Q — конечное множество формул, то мы если не оговорено противное, предполагаем, что она представляет собою конъюнк­цию ее составляющих.

Например, Q  р означает, что конъюнкция всех составляющих Q вле­чет р. В качестве правил вывода используются правила вывода исчисления предикатов первого порядка, включая следующий бесконечный класс ак­сиом:

1.p[qp];

2. p [q r] [[p q]  [q r];

3. [_ q _ p][[ _ q  p] q];

4. x p(x) p(t), где p(x) — формула и t — константа или свободная переменная для х в р(х) и p(t) означает результат подстановки t для каждого вхождения х в р(х) и

5. x[pq]  [pxq], если р — формула, не содержащая свободных вхождений х. Это логические аксиомы. Все другие аксиомы называются собственными или нелогическими аксиомами. Теория, в которой нет собственных аксиом, называется исчислением предикатов. Исчисление высказы­ваний включает только аксиомы 1,2,3.

Мы можем получить различные варианты немонотонных логических систем, добавляя к этим аксиомам все или некоторые из следующих правил немонотонного вывода:

AS1:Lpp.

AS2: L(p  Я)  (Lp  Lq).

AS3:(()Lp)L()p.

AS4: LLp Lp.

AS5:MpLMp.

Правилами вывода являются

Модус поненс; р,р  q —> q,

Универсальная генерализация: р —> p,

Необходимость: р —>Lp.

Мы получаем различные модальные системы, выбирая различные подмножества из этих формул. Наиболее слабая — модальная система Т содер­жит аксиомы AS1 и AS2. AS1,AS2 и AS4 образуют модальную систему S4, AS1,AS2, AS4 и AS5 образуют модальную систему S5. Рассмотрим монотонные правила вывода, обозначая через А и В теории.

Если S — множество формул и р следует из S и аксиом А по правилу модус поненс и генерализации, S -_рc р. Мы выводим сокращение для -_рc в виде |-.

Мы вводим оператор Th, определив его следующим образом:

Th(S)={p:S|-p}.

Оператор Th(S) обладает следующими свойствами монотонности:

1. ATh(A);

2. если АВ, тогда Th(A)  Th(B); а также

3. свойством идемпотентности Th(Th(A)) = Th(A).

Ясно, что любая классическая система удовлетворяет этим требованиям. Свойство 3 можно рассматривать как уравнение для нахождения фиксиро­ванной точки оператора, говорящее о том, что множество теорем, монотонно выводимых из теории, представляет собой фиксированную точку оператора, который вычисляет замыкание множество формул для монотонных правил вывода. Известное свойство монотонных правил вывода — это то, что Th(A) есть пересечение всех S таких, что AS и Th(S) = S, где А — любая теория первого порядка, L — язык теории, S с L — подмножество аксиом языка.

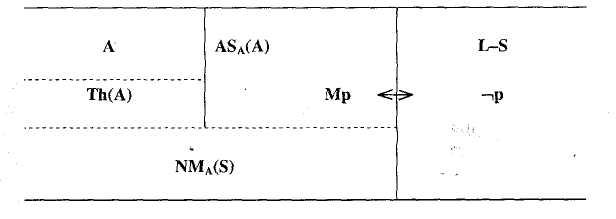
Рис 7.2. Графическое представление соотношений между теориями:

. А  Th(A), (Th(A)As_A(S))NM_A(S),

Th(A)As_A(S) = ,

(LS)-NM_A(S) = 

А  Th(A), Th(A) — множество теорем, монотонно выводимых из А

Для того чтобы иметь дело с немонотонной логикой, нам необходимо новое правило вывода. Вместо понятия выводимости |-, используемого в моно­тонной логике, мы определим оператор NM.

NM_A(S) = Th(AAs_A(S)), т.е. теория, состоящая из всех предложений, вытекающих из А и множества допущений As_A(S) (assumptions) теории S.

As_A(S) — множество допущений в S.

As_A(S) = {Mq : q L и _ qS} -Th(A).

Заметьте, что теоремы А вида Mq никогда не рассматриваются как допущения (а только как аксиомы). NM_A берет множество S и производит новое мно­жество, которое включает Th(A), но включает также много больше: все дока­зуемое из расширенного множества аксиом и допущений, которое составляет оригинальную теорию вместе со всеми допущениями, не определенными S.

Рассматривая NM_A как совокупность немонотонных правил вывода, определим по аналогии с монотонным случаем ТН(А) — множество теорем, немонотонно выводимых из А по аналогии с монотонным случаем как наи­меньшую фиксированную точку NM_A. Это определение пытается объеди­нить немонотонное правило вывода с теорией первого порядка. Определим формально ТН следующим образом:

ТН(А) = ({Z,}{S:NM_A(S) = S}.

Таким образом, множество доказуемых формул есть пересечение всех фиксированных точек NM_A.

Фиксированная точка S = NM_A(S) показана на рис. 7.2. Может случиться, теория не имеет фиксированной точки, а если точка имеется, то она не единственная.

Мы будем использовать А|~ р чтобы указать, что р  ТН(А). Будем называть FP(A) множество {S: NM_A(S) = S}.

Другой системой, позволяющей учитывать изменения теории по мере поступления новых знаний, является логика умолчаний Рейтера. Особенности логики умолчаний поясним на примере. Знание «как правило, совершенно­летние имеют паспорт» можно представить в виде следующей логической формулы: x гражданин (х)  M паспорт (х)  паспорт (х). Смысл этого вы­ражения заключается в том, что х — гражданин, х имеет паспорт, если это не противоречит другим знаниям. Теперь рассмотрим систему аксиом, состоя­щих из следующих знаний:

x гражданин (х) М паспорт (х)  паспорт (х),

x гражданин (х)  военнослужащий (х)паспорт (х),

гражданин (Александров),

военнослужащий (Александров).

Из этой системы аксиом можно сделать вывод «паспорт (Александров), т.е. что военнослужащий Александров имеет паспорт в то время как удостоверением личности военнослужащего является военный билет. В систему аксиом выведено дополнение военнослужащий (Александров). После этого делается вывод «паспорт (Александров).

В немонотонной логике основная проблема с введением логического обозначения М, Мр состоит в следующем. Пусть в базе знаний (системе ак­сиом) существуют знания (логические формулы).

{Mp_,q, Mq_ p}

{Возможно, солнечно  нет дождя}

{Возможно, дождь  нет солнца (пасмурно)}

Тогда для решения возможны две ситуации: решение, которое включает -_ р, но не включает _ q, (пасмурно, нет дождя) и решение, которое включает _ q, но не включает _ р (нет дождя, солнечно). При этом нельзя сделать вы­вод о том, может ли _ р или _ q являться решением, т.е. не определена не­подвижная точка.

В логике умолчания Рейтера формулы со знаком М используются только в предпосылках правила вывода. Рассмотрим в новой записи формулы

гражданин (х): М паспорт (х)

паспорт (х)

Как отмечается выше, при этом возможно несколько решений и возникают ситуации, когда решение нельзя определить однозначно, соответствующее решение рассматривается как один из возможных миров и называется «суже­нием» системы аксиом. Переход от одного выбранного решения к другому рассматривается как переход между возможными мирами. Общая формула:

Запись, в которой формула после знака М в предпосылке совпадает с формулой в выводе, называется нормальным умолчанием. Если (х),(х)не содержат свободных переменных, умозаключение называется закрытым нормальным умолчанием.

Модальной логикой называют раздел формальной логики, в которой наряду с утверждениями и отрицаниями (ассеторическими высказываниями) исследуются так называемые сильные и слабые утверждения и отрицания (модальные высказывания). Например, усилением ассеторического высказывания «предприятие А принадлежит ЗАО «Теллур» является высказывание «предприятие А по необходимости принадлежит ЗАО «Теллур». Ослаблени­ем данного высказывания является высказывание «предприятие А, возмож­но, принадлежит ЗАО «Теллур». Логические термины «необходимо», «воз­можно», а также «случайно», при помощи которых из ассеторических обра­зуются модальные высказывания, называются модальностями. В современ­ной логике эти термины рассматриваются как операторы, таблица истинно­сти для которых приведена ниже

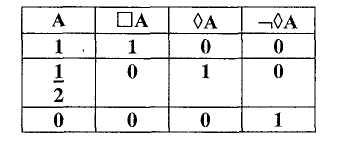
Примером формальной системы модальной логики может служить исчисление S4 Льюиса, когда интерпретацией этого исчисления является алгебраическая семантика. Исчисление S4 Льюиса является расширением классического исчисления высказываний за счет введения оператора необходимости (□) и определения оператора ◊А как ¬ d ¬ А, а также и добавле­ния трех аксиом к классическому исчислению высказываний:

□ (АВ) (□А□В),

□AA,

□А □ □А,

├A

├□А

Оператор необходимости интерпретируется как топологическая операция взятия внутренности множества. Пусть даны произвольное (непустое) универсальное множество J и множество всех подмножеств этого универсаль­ного множества, обозначаемое буквой К.

Будем интерпретировать конъюнкцию и дизъюнкцию как пересечение и объединение множеств, импликацию как объединение дополнения к А в универсальном множестве с множеством В, т.е. АВВ.

Оператор необходимости интерпретируется как топологическая операция взятия внутренности множества J. К формальным семантикам относятся семантики «возможных миров» — окрестные и реляционные. В этих семантиках используются понятия «истина» и «ложь», а необходимость определяет­ся как истинность во всех мирах, возможных относительно некоторого «данного» мира.

Рассмотрим семантику Монтегю—Скотта для модального исчисления LJ. Исчисление LJ является расширением классического исчисления высказы­ваний за счет введения оператора необходимости схемой аксиом

□ (АВ) □А □В и правила вывода

Основным понятием окрестностной семантики является понятие модальной структуры. Модальная структура — это упорядоченное множество этих трех элементов <К, о, R> где К — множество возможных миров,о — неко­торый «действительный» мир, R — отношение достижимости между эле­ментами К и подмножествами К.

В семантике LJ отношение R обладает следующим свойством: если из мира d достижимо множество миров В и множество миров С, то из D дости­жимо множество миров ВС.

Характеризуя семантики возможных миров, можно сказать, что содержащиеся в этих высказываниях утверждения относятся не только к некото­рому действительному, актуальному миру, но и к множеству достижимых из него миров, составляющих определенную его окрестность.

Исчисление S5 Льюиса получается из исчисления S4 путем добавления схемы аксиом А□◊А.

Возможный мир Р модальной структуры трактуется как множество фак­тов и связей между ними, выражаемых законами.

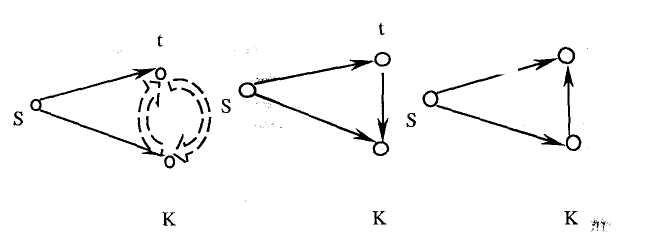
Рис. 7.3. Отношения достижимости

Описание мира можно представить как Г, где— есть классическое описание состояния, а Г — множество упомянутых законов и, возмож­но, также некоторых их следствий нефактического характера. В S5 справед­ливы соотношения:

Р◊ Р

◊P□P

□P=◊P

В семантике для S4 отношение R обладает свойствами рефлексивности и транзитивности, т.е. в модальных структурах каждый мир достижим из самого себя, и если из мира S достижим мир t, а из мира t достижим мир к, то из мира S достижим мир к. Возможные миры можно понимать как описание состояний.

Формула □A является истинной в мире S тогда и только тогда, когда она (А) истинна в каждом мире, достижимом из S. Формула истинна в модальной структуре, тогда и только тогда, когда она истинна в отдельном мире этой структуры. Формула является логически истинной, тогда и только то­гда, когда она истинна в каждой модальной структуре.

Пусть дана формула:

□p□ □p.

Чтобы решить вопрос о ее логической истинности следует рассмотреть произвольную модальную структуру с отношением R, обладающим свойствами рефлексивности и транзитивности:

□ p истинна в выделенном мире.

р истинна в каждом мире, достижимом из о.

□p истинна в каждом мире, достижимом из о, т.к. миры, достижимые из миров, достижимых из о также достижимы из о, и в них р истинна. Следовательно, □□p истинна в о. Таким образом □p□□p истинна в произвольной модальной структуре.

Семантика исчисления S5 Льюиса

Язык содержит связки , , □ и ◊. □ и ◊ — символы логической необходимости и логической возможности.

Рассмотрим формулу

□ (pq) (□р□q)

и все конечные описания состояний для этой формулы, т.е. ситуации α₁={р, q}, α₂={ р, }, α ₃={,q}, α ₄={ ,}

α ₂ ={р, } ложна, так как при таких значениях истинности ложна формула (р ) («ложь не может следовать из истины j») и поэтому ложна форму­ла □ (р q). В ситуациях α_з={ ,q} и α₄={ , } ложна формула р, следо­вательно ложна и □p, т.к. ложное высказывание не является логически необ­ходимым. Из лжи следует все, что угодно, поэтому формула истинна.

В описании состояния α₁ истинными являются формулы р q, р и q. Что можно сказать об истинности формул □ (p q), □p и □q? Возможны следующие варианты:

1. р и q не могут быть ложными (тавтологии)

2. р и q могут быть ложными

3. р может быть ложной

q не может быть ложной

4. р не может быть ложной

q может быть ложной

Таким образом, рассматриваются подстановки: переменным, кроме значений t и f приписываются значения t_n — истинно фактически и логически необходимо,

t_c — истинно фактически и логически случайно,

f_i— ложно фактически и логически невозможно,

f_с — ложно фактически и логически случайно.