Предприятие ао «Изотоп» подлежит процедуре санации.

Модус толленс отличается от модус поненс в том отношении, что мы де­лаем выводы в обратном направлении — от ложности заключения к ложно­сти посылок.

Практика применения правил вывода гильбертовского типа показала их громоздкость при производстве логических следствий из данного множества аксиом.

Вывод из множества посылок Г есть последовательность формул такая, что каждая формула, входящая в эту последовательность, является или ак­сиомой, или одной из посылок множества Г или непосредственно выводима из формул, предшествующих ей в данной последовательности. Формула выводима из множества посылок Г, если и только если существует вывод из посылок Г и естьпоследняя формула этого вывода. Более строго доказательство в формальной системе из множества аксиом А есть конечная последовательность ₁, ₂, — _n-1, _n формул, таких что _n = и каждое из _i, 1 < i > n, либо аксиома, либо следует из аксиом с меньшими номерами по одному из трех правил вывода: модус поненс (правило отделения), модус толленс и правило резолюции.

Исчисление гильбертовского типа весьма неудобно с практической точки зрения, так как шаги построения вывода очень мелки. Ни в определении понятия вывода, ни в формулировке исчисления не содержится указаний на то, к каким формулам и в каком порядке следует применять правила. Для со­кращения записи и укрупнения шагов вывода используем следующую идею: если некоторые выводы уже построены, то мы, во-первых, формулируем логические правила перехода от данных посылок к заключению и в даль­нейшем используем их в качестве блоков. Такие укрупненные правила пред­ставляют собой формальную запись правил рассуждения классической логи­ки. Рассмотрим некоторые из этих правил.

закон коммутативности, (7.17)

закон удаления дизъюнкции, (7.18)

метод рассуждения путем разбора случаев, (7.19)

—«f» означает «ложь», метод доказательства от противного. (7.20)

Пусть А, В, С, D,... совокупность логических посылок, которые предполагаются истинными, тогда предложение Г = А ВСD... также истин­но. В формальной записи это правило выражается введением конъюнкции справа, т.е.

закон конъюнкции. (7.21)

дизъюнктивный силлогизм. (7.22)

модус поненс. (7.23)

закон гипотетического силлогизма. (7.24)

конструктивная дилемма. (7.25)

сведение к абсурду (7.26)

правило резолюции (7.27)

Рассмотрим теперь в качестве альтернативного варианта систему логиче­ского исчисления LK: «Logical Kalkiil» Г. Генцена.

В исчислении секвенций, предложенном Генценом, основным понятием является понятие секвенции. Секвенция есть выражение вида Г Θ, где Г и Θ суть последовательности формул, возможно пустые.

Допустим, имеются формулы А₁,...,А_m, В₁,...,В_n. В LK-системе используется следующее представление секвенции:

А₁,...,А_m В_1;...,В_n где m,n 0.

Левая часть секвенции называется антецедентом (А₁...,А_m) а правая часть (В₁,...,В_n) — сукцедентом. Смысл секвенции в том, что если при m,n 1 выполняется A₁ и ... и А_m, то справедливо В₁ или ... или В_n. Другими сло­вами, ее можно рассматривать как формулу

A₁...A_mB₁... B_n

Если m = 0, то B₁ ... B_n считается истинной; при n=0 А₁ & & А_m

считается ложью. Другими словами —>В₁...,В_n означает, что среди B₁,...,B_n есть по крайней мере одно правильное логическое выражение, если записать это в виде формулы, то получим

В₁ ... B_n.

Запись А₁ ... А_m означает, что набор А₁,...,А_m является противоречивым. Соответствующая формула имеет вид

А₁ ... А_m.

Генценовская нормальная система логических выводов (доказательств) отлична от гильбертовской. Следует отличать символ импликации в его роли посредника при выводах от этого же символа доказываемой формулы. Поэтому вводится новый функциональный символ , читается как «дает» или «приводит к», которому будут приписаны свойства, сходные со свойст­вами символа . Некоторые часто используемые секвенции и представляю­щие их формулы приведены ниже:

Θ B₁ B₂ … . B_m;

Г А₁ ... А_n;

f.

LK-аксиома представляет собой секвенцию вида С С, где С — произвольная формула. Ниже показаны правила вывода в системе LK. В правиле вывода из секвенции, записанной над чертой, выводится секвенция, записанная под чертой. Над чертой может быть одна или две секвен­ции. Правила вывода имеют имена, например, V, T и т.д. Правила вы­вода разделяются на логические и структурные. В структурных правилах вывода логические символы не используются, а в логических правилах может быть только один логический символ (в нижней секвенции). Эти правила, в свою очередь, делятся на два типа: в первых логический символ стоит после стрелки, а во вторых— перед стрелкой. Например, показывает, что это правило, в котором символ стоит перед стрелкой в нижней секвенции. Аналогично показывает, что символ стоит по­сле стрелки в нижней секвенции.

Что касается символов  и , A(t) обозначает результат подстановки t в х. В формуле А(х) правил вывода  и  терм t должен подставляться вместо переменной х. Рассмотрим теперь правила  и . В этих правилах и — переменная, а А(и) — это результат подстановки и вместо х в формуле А(х). При этом переменная и не появляется в нижней секвенции правила и называется собственной переменной правила вывода.

Имена правил Т, С, I — это первые буквы в словах Thinning (утоньшение), Contradiction (противоречие), Interchange (взаимный обмен). Система LK позволяет для вывода использовать секвенции в обратном порядке. В отличие от прямого вывода, когда можно применять почти все правила, при обратном выводе, если исключить структурные правила, можно приме­нять максимум два правила. Тем не менее, для выполнения обратного выво­да имеется одно неудобное правило. Это правило сечения. Генцен показал, что можно обойтись и без применения правила сечения, а именно: если су­ществует доказательство, основанное на правиле сечения, то, видоизменив это доказательство, можно получить такую его форму, в которой не исполь­зуется правило сечения.

Допустим, что знания представлены логическими формулами A₁,...,A_m, a последовательность этих формул обозначается буквой Г. Чтобы проверить, можно ли на основании этих знаний вывести новый факт В, следует проверить возможность существования доказательства Г В. Если доказательст­во существует, то говорят «выражение Г В доказуемо» и записывают |- Г В. В данном случае говорят также, что В доказуемо на основании Г, и за­писывают Г |- В. Если Г — пустая последовательность (m = 0), то записыва­ют |- В и говорят, что секвенция выводима. Запись |- Гозначает, что Г — противоречивая последовательность. В правилах вывода Генцена посылки, т.е. секвенции, написанные над чертой, называются верхними секвенциями, а заключение, т.е. секвенция, написанная ниже черты — нижней секвенцией. В каждом двухпосылочном правиле имеются две верхние секвенции — ле­вая и правая. Явно выделенные из списка формулы верхних секвенций назы­ваются боковыми формулами, а явно выделенная формула нижней секвен­ции— главной формулой этого правила. Все остальные формулы, сохра­няющиеся без изменений при переходе от верхней секвенции к нижней, на­зываются параметрическими.

Все правила исчисления секвенций являются обратимыми, т.е. правила вывода, полученные из исходных заменой верхней секвенции на нижнюю, а нижней — на верхнюю, являются производными правилами.

Из теоремы Генцена об устранении (допустимости) сечения следует тео­рема о непротиворечивости исчисления секвенций.

Действительно, легко установить, что секвенция А А выводиматогда и только тогда, когда выводима пустая секвенция , но вывод последней невозможен без применения правила сечения, отсюда автоматически следует, что противоречивая формула не выводима. При записи секвенций буквы А, В, С,D используются для представления формул, а прописные бу­квы греческого алфавита Г, , Θ, П — для представления ограниченного или пустого ряда формул.

Введение импликации справа

Введение дизъюнкции справа

(7.29)

Формулы А и В называются боковыми формулами, а формула AB — главной формулой этого правила.

Введение конъюнкции справа

(7.30)

Формулы А и В называются боковыми формулами, а формула АВ — главной формулой этого правила.

Введение отрицания справа

(7.31)

Введение квантора существования справа

(7.32)

Введение квантора общности справа

(7.33)

Ослабление справа

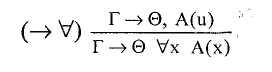
(7.34)

Сокращение справа

(7.35)

Перестановка справа

(7.36)

Введение импликации слева

(7.37)

Введение дизъюнкции слева

(7.38)

Введение конъюнкции слева

(7.39)

Введение отрицания слева

(7.40)

Введение квантора существования слева

(7.41)

Введение квантора общности слева

(7.42)

Правила, содержащие кванторы, называются кванторными. Условия, что собственная переменная не должна входить в нижнюю секцию в правилах «V справа» и «3 слева» будем называть ограничением на собственную пере­менную для этих правил.

Ослабление слева

(7.43)

Сокращение слева

(7.44)

Инверсия слева

(7.45)

Сечение

(7.46)

Формула D называется высекаемой формулой этого правила.

Вывод в исчислении секвенций строится последовательным применени­ем описанных выше правил. Всякая секвенция вида А А называется начальной секвенцией или аксиомой. Выводом Р в исчислении предикатов первого порядка или LK-выводом называется дерево секвенций, удовлетворяющее следующим условиям:

• самые верхние секвенции в Р являются начальными секвенциями,

• каждая секвенция в Р, кроме самой нижней, является верхней секвенцией некоторого непосредственного вывода, нижняя секвенция которого также принадлежит Р. Система LK является примером, когда на основе данного критерия лучше выбрать обратный вывод. Однако имеется неудобное правило — правило сечения, когда необходимо создать отсутствующую формулу С. Однако теорема об устранимости сечения позволяет преодо­леть эту трудность.

Исчисление секвенций составило на первых порах основу поиска логиче­ских следствий из некоторого множества аксиом.

Рассмотрим пример применения описанных выше правил для поиска вы­вода формулы

. (7.47)

Нам нужно установить, доказуема ли секвенция

(7.48)

Согласно правилу () сведем эту задачу к более простой:

(7.49)

Верхнюю секвенцию получим по правилу ():

(7.50)

Верхнюю секвенцию в полученном выражении мы можем получить, если сможем построить вывод более простой секвенции (АВ),А,B, т.е.

(7.51)

Воспользовавшись правилом (), сведем задачу к выводу следующей секвенции:

О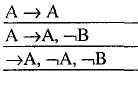бъединяя шаги приведенного анализа, мы получим дерево вывода:

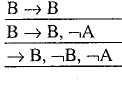(ослабление справа) (ослабление справа) () ()

()

(7.52)

Алгоритмы проверки выполнимости или общезначимости формулы явно или неявно используют понятие семантического дерева. Если дано конеч­ное или счетное множество высказываний Р - {р₁ ..., р_n ...}, то семантиче­ское дерево — это бинарное корневое дерево, удовлетворяющее следующим условиям:

• каждая дуга помечена позитивной или негативной литерой, взятой из Р;

• литеры, которыми помечены две дуги, выходящие из одного узла, проти­воположны;

• никакая ветвь не содержит более одного вхождения каждой литеры;

• никакая ветвь не содержит пару противоположных литер.

Конечное семантическое дерево полно, если каждый его лист соответствует некоторой тотальной, т.е. всюду определенной интерпретации.

Для того чтобы определить, выполнима ли формула А, тривиальный алгоритм требует просмотра некоторого полного семантического дерева, соот­ветствующего конечному множеству высказываний, встречающихся в А.

Секвенция доказуема тогда и только тогда, когда соответствующее ей дерево поиска доказательства замкнуто. Имеется теория поиска доказательств — инференциальный анализ. Однако метод поиска доказательства для сложных формул дает чрезмерно большое дерево поиска и требует большой памяти и времени реализации на компьютерах. Сложность алго­ритмов поиска вывода в таких системах экспоненциально возрастает по мере увеличения числа переменных.